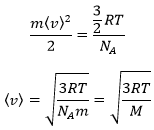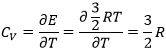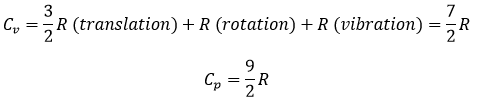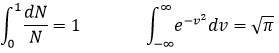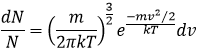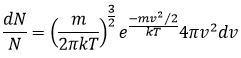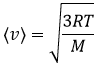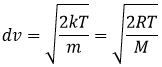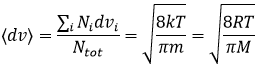Les états de la matière:

Nous pouvons considérer trois différents états : gaz, liquide et solide et un mélange d’entre eux. Une différence importante entre les trois états de la matière est le volume qu’ils occupent. Un gaz prend tout l’espace disponible, un liquide prend la forme de son récipiant et un solide a sa propre forme. C’est le résultat des interactions entre les molécules qui composent la matière. La composition joue un role mais il n’est pas le seul paramètre à considérer. Simplement défini, la composition de l’eau, de la glace et de la vapeur d’eau est la même (H2O), mais les interactions entre les molécules de H2O sont différentes. Le but de ce chapitre est de décrire les différents états de la matière et les transitions entre eux.

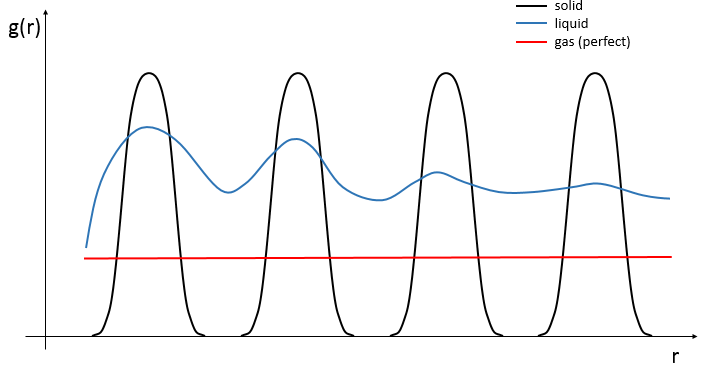
L’agencement de la matière peut être définie à partir de la répartition des atomes de voisinage entre eux. Si nous nous concentrons sur un atome spécifique, la probabilité g (r) de trouver un ou plusieurs atomes à une distance r donnée de l’atome diffère fortement entre les liquides, les solides et les gaz.

Dans un solide les atomes sont organisés et ne se déplacent pas librement (ils peuvent vibrer autour de leur position). La répartition dépend de la géométrie de la matière solide mais elle est caractérisée par des pics élevés localisés à des distances régulières avec g (r) »0 entre eux. Dans un liquide nous pouvons voir qu’il ya encore des couches de voisins autour d’un atome donné mais que l’ordre est moins important. En outre les pics disparaissent après quelques couches. Un liquide est donc caractérisé par un ordre à courte distance et le désordre à longue portée. Le nombre moyen de voisins dans un liquide est en général plus faible que dans un solide. Dans un gaz parfait les atomes ne se subissent pas l’un  l’autre et n’ont aucune interaction entre eux. La probabilité de trouver un atome à une distance donnée les uns des autres est donc égale à une distance quelconque. Dans un gaz réel cependant les interactions peuvent exister et g (r) varie légèrement.

Gaz :

Nous sommes entourés par les gaz. Nous pouvons les déplacer quand nous nous dirigeons mais ils appliquent une résistance à nos mouvements. Même lorsque nous ne progressons pas il ya une pression de l’air sur nous. Nous n’y pensons pas parce que nous sommes habitués à cela et notre corps applique une force pour contrer cette pression. Si nous étions soumis à un vide nous irions nous élargir en raison de cette force. Le fait que l’air exerce une pression a été prouvé par Otto Von Guericke (XVIIe siècle). Il construisit deux demi sphères se collant parfaitement pour ne plus en faire qu’une. Il a enlevé l’air à l’intérieur d’elles et a demandé à son seigneur pour essayer de l’ouvrir à l’aide de quatre chevaux. Ils n’ont pas réussi. En remettant de  l’air dans la sphère il était, à nouveau, possible de l’ouvrir.

Il ya encore des objets que nous utilisons souvent basés sur ce principe : des ventouses pour la plomberie, celles pour mettre votre GPS sur le pare-brise. Le vide que nous créons n’est jamais complet et la force nécessaire pour retirer une ventouse dépend du degré de vide que nous avons créé. Il devient  plus facile de les enlever une fois nous laissons pénétrer un peu d’air dans la ventouse.

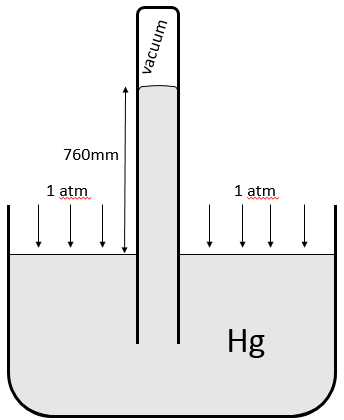
Une pression est une force appliquée sur une surface. La pression exercée par l’air dans des conditions standards est d’une atmosphère ce qui équivaut à 101 325 pascals, le plus souvent donnée en hectopascals (1013 hPa). Nous mesurons également la pression d’un gaz avec torr. 1 atm = 760 torr. L’unité de torr est la hauteur, en mm, qui atteint le mercure dans un tube  vide quand une pression est appliquée sur le reste de sa surface dans la disposition ci-dessous:

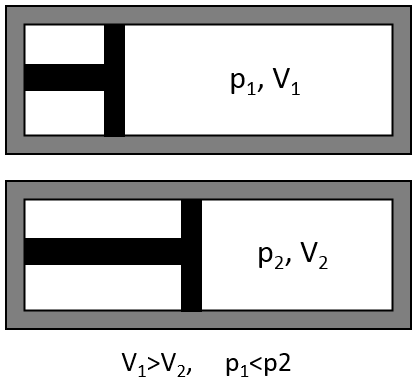
Il existe une relation entre le volume d’un gaz et sa pression. Boyle a déterminé que, à une température constante, la multiplication de la pression d’un gaz par son volume donne une constante.

Si le volume diminue, la pression augmente dans la même proportion :

Charles Gay Lussac observa, d’autre part, que le volume des gaz dépend de la température et que, peu importe le gaz, leur volumes tendent à 0 lorsque la température va vers 0 K (il a étendu les courbes en fonction des  changements de d’Etat des gaz).

Un troisième contributeur à la compréhension des gaz est Avogadro qui a indiqué que, à une température et une pression donnée, le volume d’un gaz est proportionnel au nombre d’atomes qu’il contient :

Considérant tout cela la loi des gaz parfaits a été établi :

Cette loi est limitée aux gaz dilués et nous considérons que les particules sont ponctuelles, lointaines et qu’il n’y a pas d’interaction entre eux.

Si l’on considère plusieurs gaz Dalton a montré que la pression totale est donnée par la somme de leurs tensions individuelles.

En conséquence si l’on considère un mélange de deux gaz :

La pression d’un composant particulier du gaz est proportionnelle à sa concentration dans le gaz :

Théorie cinétique des gaz :

On peut mesurer la pression exercée par un gaz sur une surface. Comme expliqué, précédemment, une pression est une force appliquée sur une surface. Une force est une masse multipliée par l’accélération. Une accélération est la variation de vitesse pendant un temps:

A noter que seule la composante de la vitesse perpendiculaire à la surface affecte la pression. Les deux autres composants n’ont pas d’influence sur cette surface particulière :

Nous faisons plusieurs hypothèses sur les particules du gaz :

-Les particules sont de petites tailles et leur volume est négligeable par rapport au volume du gaz. Elles sont considérées comme des points.
-Elles ont toutes la même masse m.
-Elles ont une vitesse constante et vont dans des directions aléatoires. Nous pouvons définir une vitesse moyenne <v>.
-Les particules ne sont pas interagissantes ensemble.
-Toutes les collisions sont purement élastique : il n’y a aucune perte de vitesse ou de l’énergie
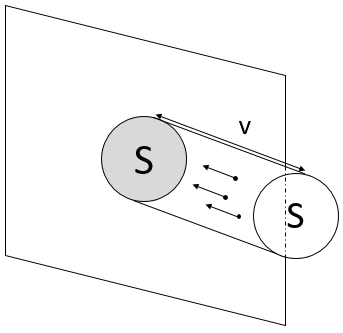
Pour déterminer la pression sur une surface S de l’une des parois, on considère que les particules qui sont capables de frapper cette surface dans une période de temps dt. Par conséquent, on ne considère que la particule présente dans un petit cylindre en face de la surface :

Lorsqu’une particule frappe la paroi, il y a une collision élastique et les particules remontent à la même vitesse. Au cours d’une période de temps la vitesse de particules a des changements par rapport à v -v. La force appliquée sur la surface par une particule est ainsi :

Dans le cylindre, il existe un nombre donné de particules :

N/V est la densité de particules dans le gaz. Parmi celles-ci seulement les particules allant dans la direction x sont importantes pour nous et parmi elles seulement les particules allant dans la direction de la surface (pas dans le sens opposé) induisent une pression sur la surface. Une multiplication par 1/6 est ainsi appliquée pour déterminer le nombre de particules incidentes sur la surface. La pression est donc :

Dans cette équation, nous reconnaissons l’énergie cinétique E_k=mv²/2. Garder à l’esprit que N = n.NA, on peut écrire :

Par conséquent on voit que l’énergie cinétique des particules dans un gaz est directement proportionnelle à la température :

A partir de là on voit également que la vitesse moyenne des particules est liée à la masse :

Cela signifie que dans un gaz à une température donnée les particules de l’oxygène et de l’azote ne se déplacent pas à la même vitesse. Par exemple : un ballon gonflé à l’azote (N₂, M = 28) se dégonfle plus rapidement qu’un ballon rempli d’oxygène (O₂, M = 32)

Cette propriété est utilisée pour enrichir l’uranium, à savoir obtenir une plus grande proportion d’un isotope de l’uranium. Compte tenu d’un volume de gaz contenant ²³⁵UF₆ et ²³⁸UF₆, une plus grande proportion de 235UF6 passera par un petit écart car il a une vitesse plus grande que²³⁸UF₆. Ce processus est l’effusion : une séparation sur la base de la vitesse des particules.

La capacité de chaleur (au V = cst) est l’énergie nécessaire pour augmenter la température d’une mole de gaz de 1° est :

La capacité thermique (p = cst) est :

Dans un gaz monoatomique toute l’énergie est utilisée pour augmenter la vitesse des particules.

Gaz diatomiques :

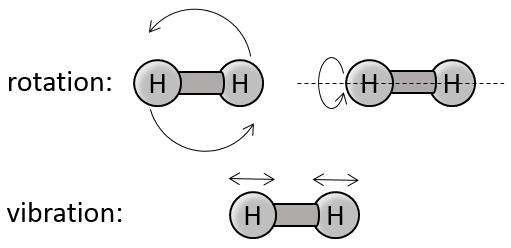
Pour des molécules de plus d’un atome l’énergie cinétique est subdivisée en trois directions (1/2R) par direction.

Si un gaz diatomique est chauffé l’énergie est utilisée par plusieurs processus :

1) traduction/accélération: la vitesse/l’énergie cinétique de la molécule augmente.
2) rotation et vibration :

Il existe deux angles de rotation l’énergie nécessaire pour faire tourner est 2 * 1/2R

Si les molécules vibrent elles ont une énergie potentielle. L’énergie obtenue à partir du chauffage est ainsi répartie en énergie cinétique et énergie potentielle. L’énergie requise pour vibrer est donc aussi 2 * 1/2R.

Les valeurs de Cv et Cp sont donc plus élevées que pour un gaz monoatomique :

Donc si nous donnons de l’énergie à Ne et N2, lequel des  gaz devrait chauffer plus ? N2 utilise l’énergie de chauffage pour accélérer  mais aussi pour vibrer et effectuer une rotation. Ne  utilise toute l’énergie comme énergie cinétique et donc chauffera plus que N2.

Répartition de Maxwell-Boltzmann :

Dans les calculs que nous avons fait nous avons  supposé que toutes les particules d’un gaz ont été touchées de manière identique par la chaleur. En réalité, la capacité thermique dépend de la température mais  tend  à 7/2R quand T tend à l’infini. L’explication :

Les particules peuvent avoir différents niveaux de l’énergie cinétique. Lorsque l’énergie est fournie toutes les particules sont également excité. Une proportion de leur population augmente son énergie cinétique d’un niveau (ou plus éventuellement). Au ok (zéro absolu), toutes les particules sont au niveau le plus bas et ne bougent pas. Elles sont congelés.

La population sur le deuxième niveau est donnée par :

ΔE1 est la différence d’énergie entre le niveau 1 et le niveau 0. k = R / NA est la constante de Boltzmann. En général la population est donnée par :

La distribution de la vitesse des particules dans les niveaux d’énergie sont données par la loi de distribution de Maxwell-Boltzmann. A partir de ce qui est dit plus haut on peut ainsi déterminer la variation du niveau en fonction de la vitesse :

Avec A une constante indéterminée nous pouvons écrire cette équation différemment :

Il est possible d’intégrer cette équation sachant que :

Cela signifierait que A=(m/2πkT)^1/2. Cependant la vitesse possède trois composants. En conséquence la distribution est :

De même pour la probabilité de présence des électrons pour les orbitales électroniques nous intégrons sur une sphère et il faut multiplier cette équation par 4πv². Nous allons ainsi obtenir la proportion de dN particules sur le nombre total de N particules avec une vitesse donnée  dv :

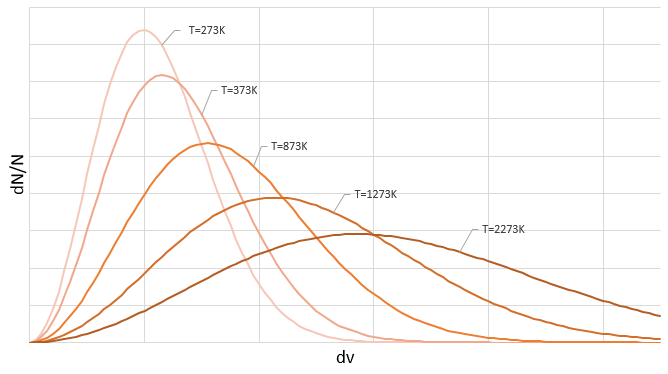
On peut voir sur cette figure que la vitesse moyenne augmente avec la température comme il a été déterminé précédemment dans la relation :

de la loi des gaz parfaits. La vitesse la plus probable se trouve au maximum des courbes quand le DN/N/dv = 0, soit à :

La vitesse moyenne que nous trouvons est un peu plus petite que celle obtenue à partir de la loi des gaz parfaits :

gaz réels :

La loi des gaz parfaits fonctionne bien pour les gaz dilués. Si nous augmentons la pression ou la température des gaz nous voyons des déviations de la loi des gaz parfaits :

Il est parce que le nombre d’interactions entre les particules devient moins négligeable. Les interactions peuvent être attractives ou répulsives mais sont faibles par rapport à l’énergie de liaison par exemple. Les interactions peuvent être entre dipôles induits ou entre dipôles permanents :

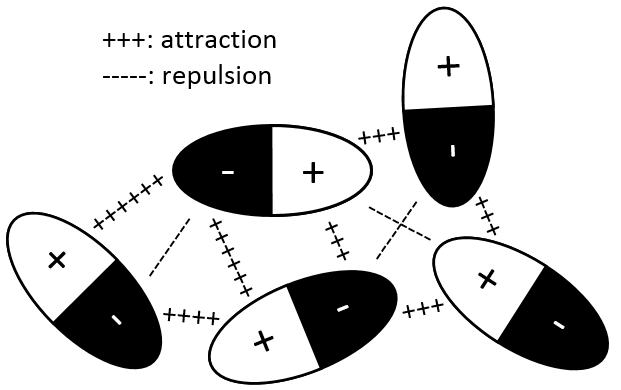
Interaction dipôle permanent- dipôle permanent

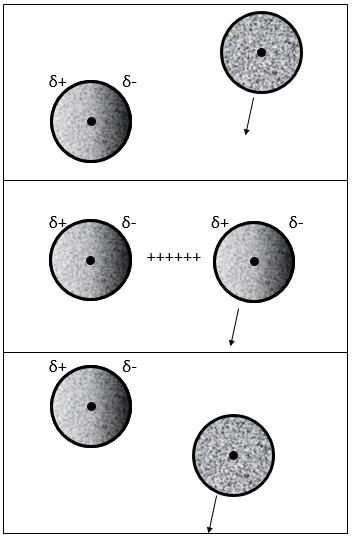
Dans ce cas les molécules composant le gaz possèdent déjà un moment dipolaire. Les charges δ + et δ-  de molécules qui passent près les unes des autres interagissent : une attraction est induite entre les charges opposées et une répulsion entre les dipôles de même charge :

                                          interaction dipôle induit-dipôle induit

Les électrons près d’un noyau sont, statistiquement, également répartis autour du noyau. En d’autres termes le nuage d’électrons est sphérique et la densité d’électrons est identique dans toutes les directions. Cependant les électrons sont constamment en mouvement et les hétérogénéités de la charge peuvent apparaître temporairement. En fait l’apparition de ces dipôles est fréquente mais dans la moyenne leur moment dipolaire est annulé.

Quand un atome passe près d’un autre atome, montrant un dipôle, il adapte son nuage d’électrons envers  ce dipôle pour réduire la répulsion entre eux :

c

En général, les interactions sont favorables entre les particules d’un gaz. Les particules ont tendance à rester à proximité les unes des autres en diminuant la pression à l’égard d’un gaz parfait.

D’autre part les particules ont un volume approprié et les autres particules ne peuvent pas pénétrer dans ce volume. Dans la loi des gaz parfaits les particules ont été considérées comme des points avec un volume négligeable.

Il en résulte que, avec l’augmentation des interactions, la pression augmente plus rapidement que pour un gaz parfait.

Au lieu de la loi de gaz parfait PV = nRT nous devons considérer l’équation  de van der Waals pour les gaz réels :

Dans le terme de pression le + a (n / v) 2  exprime les interactions entre les particules. (a) représente la force d’interaction dont la valeur dépend du type d’interaction, la taille des molécules, le nombre d’électrons, etc.. (n/V)2 représente la « densité » des interactions et devrait en fait être n / V * (N-1/V) tel que chaque particule du volume (n) peut interagir avec toutes les autres particules (n-1) mais que le n est proportionnel à NA; la différence est négligeable.

En terme de volume b représente le covolume d’une particule. Le volume vide où les particules peuvent se déplacer est le volume total moins le volume des n particules composant le gaz.

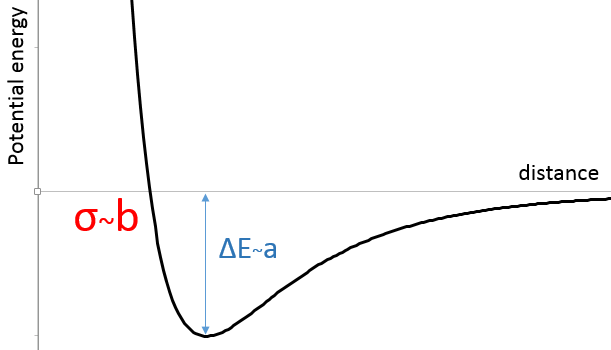
Dans la figure du potentiel de Lenard Jones nous pouvons relier a et b à l’énergie de la fosse et à la distance d’approche plus petite σ :

L’enthalpie de vaporisation ΔHv reflète l’énergie nécessaire pour transformer un liquide en gaz. Il nécessite plus d’énergie pour vaporiser les molécules avec des interactions fortes que de molécules avec dipôles induits seulement. Les sprays d’eau sont vendus à cause de cette propriété : une fois sur notre peau les petites gouttelettes se vaporisent, prennent l’énergie de la peau, diminuant sa température et donnant une sensation de fraîcheur.

Le processus inverse est la liquéfaction. Les molécules de gaz sont distantes les unes des autres. Pour devenir liquide les particules se déplacent dans la fosse  de potentiel. Toutefois, si elles ont une trop grande énergie cinétique (dépend de la température), ils vont sortir de l’autre particule. Il faut de l’énergie pour quitter la fosse de potentiel. En conséquence la liquéfaction implique une diminution de la température.