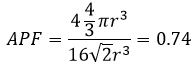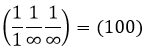Une caractéristique des solides est qu’ils ont leur propre forme. Les Liquides prennent la forme de leur destinataires et les gaz prennent tout l’espace disponible. Donc les solides ont leur propre forme, mais certains sont malléables, peuvent être coupés, être froissés, brisés ou peuvent être très rigides. Comme expliqué au début de ce chapitre tout est une question d’interactions entre les éléments du solide.

Il ya différents types de structures pour les solides :

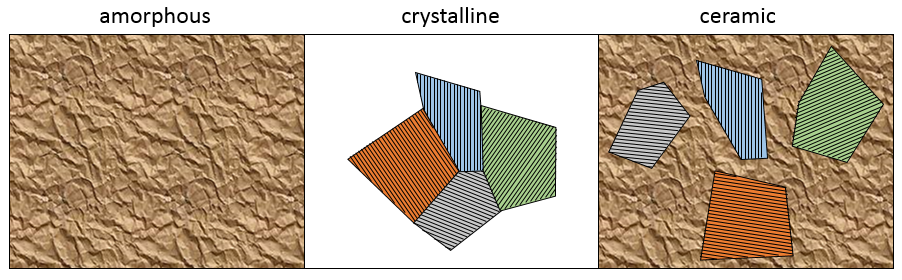
Amorphe : arrangement désordonné des atomes

Crystalline : arrangement ordonné d’atomes. Dans un monocristal, le solide ensemble a augmenté d’un point et il y a un seul arrangement. Cependant il est difficile d’obtenir un monocristal parce que plusieurs points de croissance peuvent développer des cristaux simultanément avec des orientations différentes. Plusieurs cristaux peuvent se développer dans des directions différentes et coexister dans un solide.

Céramique : quelques cristaux dans un réseau amorphe. C’est un mélange des deux types de structure citées plus haut.

La structure d’un solide peut être déterminée par la diffraction des rayons X.

Les solides peuvent être constitués de différents types de liaisons :

Métallique : les électrons peuvent se déplacer le long du solide. Ils sont très compacts et présentent des propriétés identiques dans toutes les directions.

Ionique : les anions sont entourés par des cations et vice versa. Dans le cas des ions sphériques dont les propriétés sont identiques dans les trois directions.

Covalente : les électrons sont localisés entre les noyaux dans les liaisons entre les atomes. Les atomes ne peuvent pas se déplacer librement. Ils sont moins denses que les solides ioniques ou métalliques en raison de la longueur de la liaison et de l’orientation imposée.

Moléculaire : il n’y a aucune règle spécifique à lier. Dans les solides moléculaires, les molécules peuvent se déplacer facilement.

Réseaux cristallins :

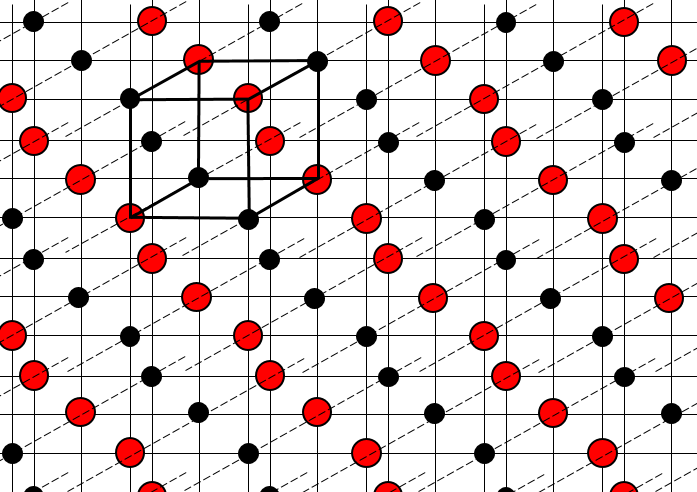
la structure des cristaux peut être définie par le plus petit constituant reproductible du réseau. NaCl est un solide ionique. Chaque Na est entouré par 4 Cl et vice versa. Le plus petit constituant reproductible du réseau est un cube en 4 Na et 4 CL, les atomes se trouvant dans les coins du cube.

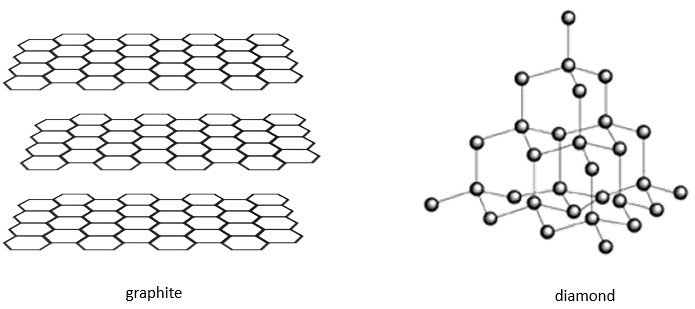
Il existe différentes structures de base pour les solides. En général un composé signifie une structure cristalline. Les cristaux de sel de NaCl ont une structure cubique. Le carbone peut avoir deux structures différentes : le graphite (hexagonales) et le diamant (cubiques face centrée). Dans le graphite il existe des interactions faibles entre les feuilles de carbone ce qui les rend faciles à séparer.

Alors que les atomes sont les mêmes, les propriétés du diamant et du graphite sont très différents. Le diamant ne conduit pas l’électricité, ne se casse pas et est transparent. Leur couleur et leur opacité dépendent des impuretés. La Graphite conduit l’électricité (les électrons de l’orbitale p ne sont pas liés et peuvent se déplacer le long des plans), se brise (les plans peuvent glisser les uns sur les autres) et est opaque.

Trois paramètres sont à prendre en considération pour trier les cristaux : les longueurs des côtés (a, b et c) de la structure, les angles entre les côtés (α, β et γ) et la position des atomes dans la structure. Les paramètres géométriques donnent 7 systèmes réticulaires indiqués ci-dessous, tandis que la position des atomes les sub-divisent en 14 réseaux de Bravais

Les différents types de structures sont les suivantes :

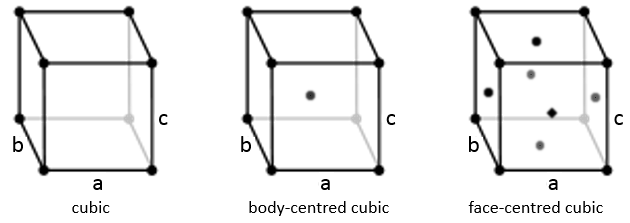
Cubique :

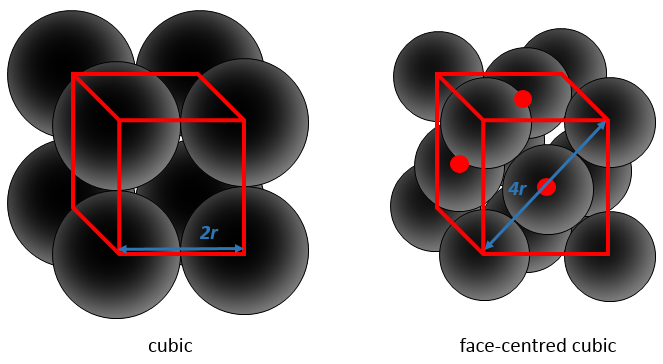
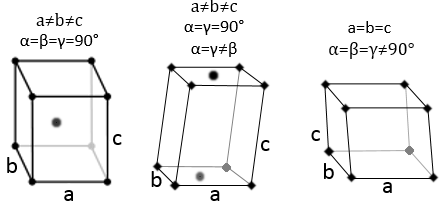
Dans la structure cubique les longueurs des côtés sont égales, a = b = c et α = β = γ = 90°. Si un atome est au milieu du cube nous appelons cette structure corps centré. Si un atome est au milieu de chaque face nous l’appelons  face centrée.

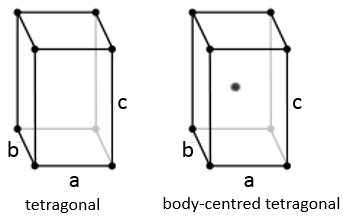
Quadrilatère :

Quand un côté a une longueur différente de celle des deux autres (a=b≠c ), la structure est appélée  quadrilatère. Il existe aussi un corps centré pour cette structure.

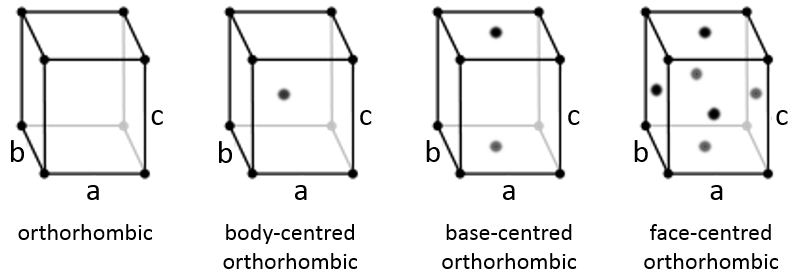
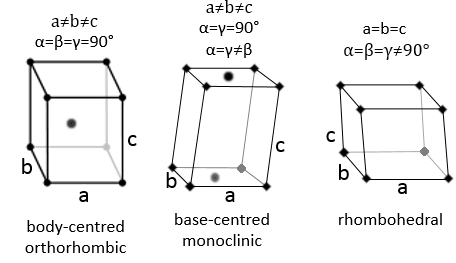
Orthorhombique :

Les angles sont encore de 90 ° mais aucune des trois longueurs caractéristiques  n’est égale (a ≠ b ≠ c). Dans le cas de structures orthorhombiques une structure supplémentaire existe : la structure de base centrée. Dans cette structure les deux côtés opposés présentent un atome au niveau de leur centre. Les deux autres côtés ne le font pas.

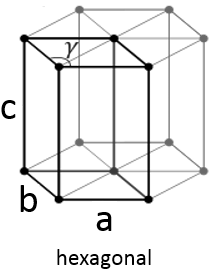
Hexagonal :

Cette structure est appelée hexagonale mais aucune de ses faces n’est hexagonale. Toutefois si vous assemblez trois d’entre eux vous obtenez un prisme hexagonal. La base et la face supérieure sont en forme de losange (a = b) avec un angle γ = 120 °. Les autres faces de la structure sont rectangulaires (a = b≠c) ou carré (a = b = c).

Rhomboédrique :

En ce qui concerne les structures cubiques, a = b = c et les angles sont égaux mais dans une structure rhomboédrique les angles  ne sont pas droits : α = β = γ ≠ 90°.

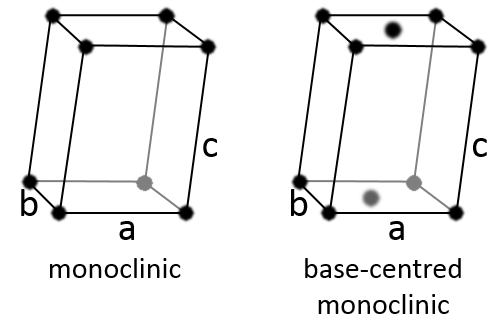
Monoclinique :

Dans ce cas deux angles sont égaux à 90° mais le troisième angle n’est pas droit. Les côtés ont des longueurs différentes a ≠ b ≠ c.

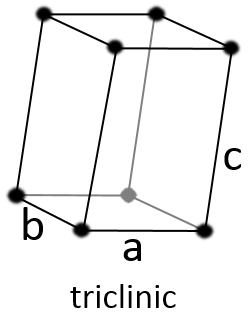
Triclinique :

Les angles α ≠ β ≠ γ ≠ 90° sont différents et il n’y a aucun angle droit. Les longueurs sont également différentes a ≠ b ≠ c.

Compacité (atomic packing factor)

Elle est déterminée par le rapport entre le volume des atomes dans le cristal et le volume total :

Considérant les atomes sphériques une partie du cube est inévitablement vide. Les figures ci-dessus sont schématiques et dans un solide réel les liaisons ne sont pas aussi longues. Nous devrions voir quelque chose comme ceci :

Cette proportion varie d’un solide à l’autre. A titre d’exemple nous allons considérer une structure cubique à faces centrées dans laquelle tous les atomes ont la même taille et le même rayon r. La longueur du cube est un volume et est ainsi h a³.

La longueur de la diagonale est de 4R et à partir du théorème de Pythagore, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés d’un triangle. Par conséquent :

Nous savons que le volume total du cube :

Nous avons juste besoin de déterminer combien d’atomes sont dans la structure. Dans chaque coin du cube il y a 1/8 d’un atome. Comme Il existe huit coins alors nous pouvons dire qu’il y a le volume d’un atome au total pour les coins. Au centre des faces il y a la moitié d’un atome. Comme Il y a 6 faces nous pouvons dire qu’il y a 3 atomes supplémentaires, par conséquent il y a 4 atomes dans le cube. Le volume  d’un atome est = 3.4 π r³. L’APF, pour cette cubique face centrée, est donc :

Par cette structure particulière, environ un quart du cube est vide. Il en est de même pour la structure hexagonale, il atteint un tiers pour la cubique corps centré et la moitié  pour la cubique :

– Hexagonale compacte : 0,74
– Cubique à faces centrées : 0,74
– Cubique à corrps centré : 0,68
– Cubique simple : 0,52

Indices de Miller :

les indices de Miller forment un système de notation pour les plans de réseaux cristallins. Il est principalement utilisé en cristallographie et je ne vais pas le développer intensément ici. Les indices de Miller sont un trio de 3 entiers, écrites (hkl). Considérant un coin d’une structure cristalline, disons une cubique, sous forme de base de notation(000), l’axe suivant les côtés du cristal. Cette base n’est donc pas toujours orthogonale si l’un des angles α, β et γ n’est pas droit. Dans le cas d’une structure cubique la base est orthogonale.

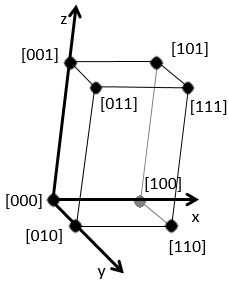
En se déplaçant dans la direction x nous allons trouver un atome après une distance a = 2r. Il est le même si nous nous déplaçons dans les directions y ou z. Pour les indices de Miller, les coordonnées x, y et z sont divisées par les dimensions de la structure a, b et c respectivement :

L’atome sur l’axe des x est à l’emplacement [100] (ce n’est pas un indice de Miller mais plutot une coordonnée). L’atome sur l’axe des y est sur le [010] et l’atome sur l’axe Z est le [001].

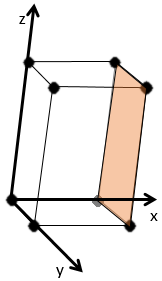
Les indices de Miller (hkl) décrivent un plan en disant où il croise l’axe x, y et z. Compte tenu du plan suivant :

nous voyons qu’il est parallèle à l’axe de y et z et qu’il croise l’axe de x à x = 1. Comme le plan est parallèle à Y et Z ils ne se croisent jamais. Nous considérons que ce serait fait à y = ∞ et z = ∞. Pour obtenir les indices de Miller nous prenons 1 sur ces valeurs :

Si les valeurs négatives sont utilisées nous les mettons avec des signes + au lieu de mettre en – un signe moins :

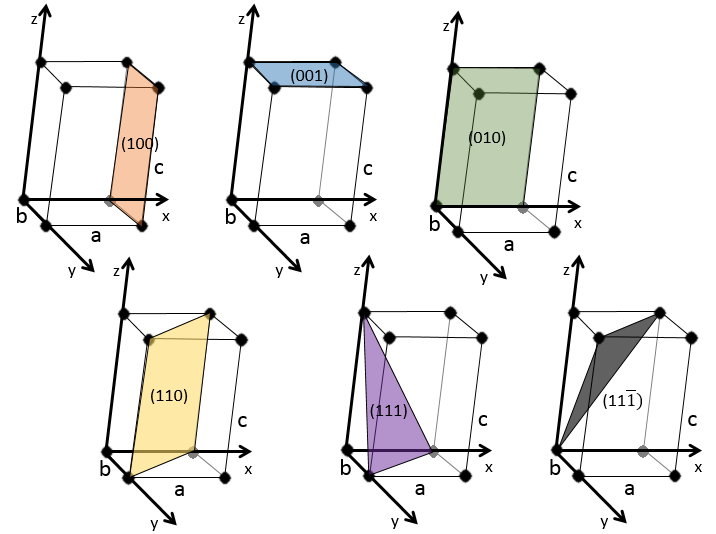
quelques exemples de plans :

Exercices :

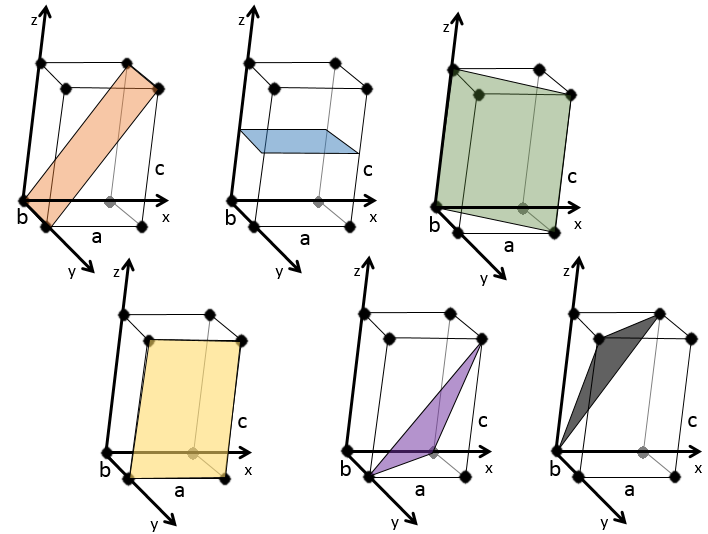
1. Comment appelez-vous ces structures ?

2.. Donnez les indices de Miller pour les plans suivants :

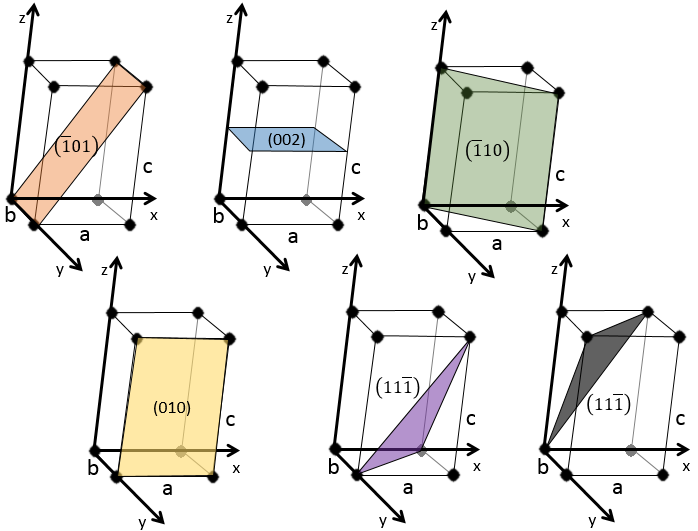
Réponses :

1:

2 :

Pour la première, le plan montré passe par l’axe y. Par conséquent nous devons le traduire. Par défaut nous traduisons en suivant l’axe des x par une seule longueur de a  à gauche.

Pour la seconde le plan est placé sur le milieu de la structure, à l’horizontale. Rappelez-vous que nous prenons l’inverse de la position : 1/0,5 = 2.

En ce qui concerne 3 le troisième plan passe par un axe. Nous traduisons le plan pour obtenir la bonne réponse.

Les deux derniers plans ont les mêmes indices de Miller. Ils sont parallèles et se confondent si nous appliquons une traduction dans la direction z.