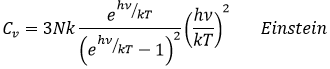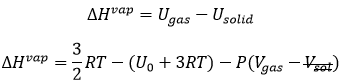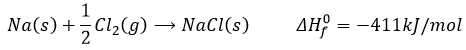Dans les gaz, la capacité thermique est une résultante des mouvements latéraux , de la vibration et de la rotation des atomes.

Dans un solide, il n’y a pas de mouvements latéraux des atomesq ni de rotation. Les atomes peuvent vibrer autour de leur position d’équilibre. La vibration implique une énergie potentielle et une énergie cinétique, chaque terme participant pour ½ R. Comme un solide a 3 dimensions :

                                                                    C_v=3R

Cependant, cette égalité n’est pas vrai à des températures basses. Elle est liée à la radiation du corps noir. Dans ce cas, la capacité thermique est donnée par :

Un corps noir est un corps idéalisé qui absorbe tout le rayonnement électromagnétique (de toute fréquence). Il émet uniquement un rayonnement appelé rayonnement du corps noir qui dépend de la température seule. Un modèle pour le corps noir est une cavité avec une petite ouverture.

Le rayonnement pénétrant dans la cavité sont piégés à l’intérieur en raison de la géométrie de tis et / ou l’absorption du rayonnement par les parois de la cavité.

A une température fixe et compte tenu de l’équilibre thermique, le trou peut permettre à une partie du rayonnement de fuite à partir du corps noir. Il est le rayonnement du corps noir, et il ne dépend que de la température. En raison de la taille du trou en ce qui concerne le corps, échappant à la radiation a un effet négligeable sur l’équilibre de la radiation à l’intérieur de la cavité.

Le U0 de l’énergie réticulaire ou énergie du réseau est l’énergie du solide à T = 0K. L’énergie du solide à une température donnée est

Nous ne pouvons pas mesurer U0 mais nous pouvons rapprocher sa valeur de l’enthalpie de sublimation: de déterminer l’énergie du solide, nous briser toutes les liaisons pour obtenir le gaz.

Le dernier terme provient de la dilatation du solide dans le gaz. Le volume de la matière solide est négligeable en ce qui concerne le volume du gaz. Si l’on considère un gaz parfait, alors PV = RT. Par conséquent,

 Nous pouvons aussi trouver l’énergie réticulaire avec le cycle de Born-Haber a expliqué dans une section précédente.

Pour un solide avec plusieurs éléments, par exemple un solide ionique, le calcul est plus complexe: il existe deux ou plusieurs gaz et interactions électroniques (liaisons ioniques, de répulsion).

Le cycle de Born–Haber :

Les atomes forment des solides car cela conduit à une diminution de leur énergie. Un moyen de quantifier cette stabilisation est le ΔH⁰_Le,  l’énergie de réseau, à savoir l’énergie requise pour former un solide à partir des ions gazeux.

Cette énergie est négatif et ne peut être déterminée expérimentalement. La manière habituelle de le déterminer est de construire le cycle de Born-Haber. Ce cycle est construit à partir des transformations de base des constituants, en les prenant séparément et commençant à partir de leurs états normaux. Plusieurs transformations peuvent être envisagées :

 – Sublimation: transformation de l’état solide à l’état gazeux
– Vaporisation: transformation d’un liquide en un gaz
– Électroaffinité: l’addition d’un électron à une particule de gaz
– La dissociation: la séparation de deux atomes
– Ionisation: la libération d’un électron à partir d’un substrat

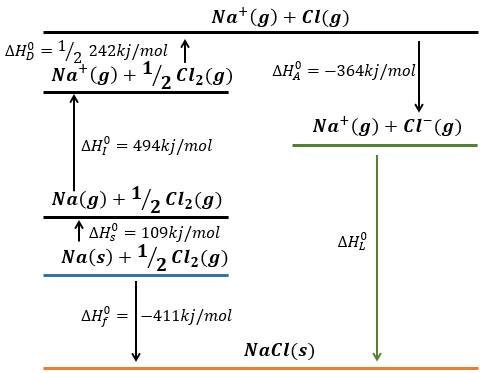
Bâtissons le cycle de Born-Haber de NaCl. Nous voulons déterminer l’enthalpie de cette réaction :

Pour ce faire, nous partons d’une réaction avec une enthalpie connu. Nous savons que l’enthalpie de réaction pour former le solide à partir de Na (s) et Cl (g) est :

La transformation de Na (s) à  Na⁺(g) est réalisée en deux étapes: d’abord la sublimation du solide à un gaz

Et puis l’ionisation du gaz

Il existe deux étapes pour obtenir ainsi Cl^–(g) à partir de Cl₂(g). La première étape est la dissociation des deux atomes de Cl₂. Comme nous avons seulement besoin d’un atome de chlore, l’enthalpie de dissociation est divisé par 2.

La deuxième étape consiste à ajouter un électron à Cl (g) (électroaffinité)

Cette énergie est fortement négative parce que le chlore atteint l’octet. Maintenant, nous avons les deux ions gazeux. Nous avons juste besoin d’additionner l’enthalpie de toutes les étapes  pour obtenir l’énergie du réseau. Le cycle de Born-Haber est souvent représenté de cette façon: