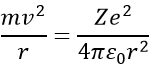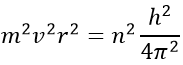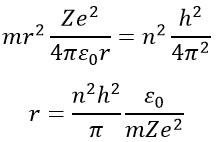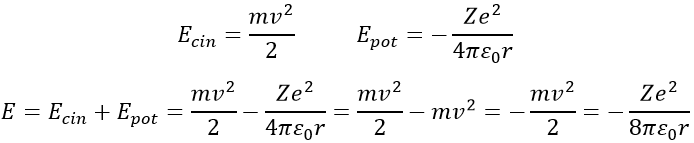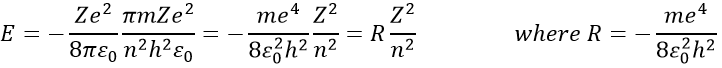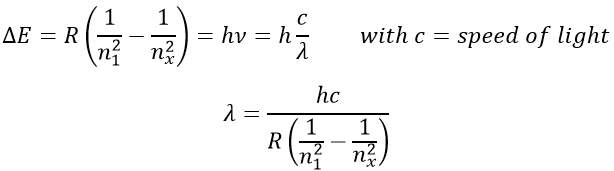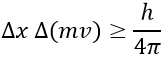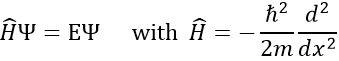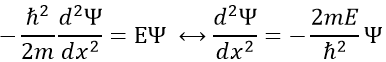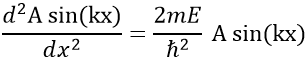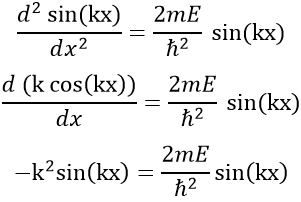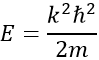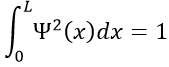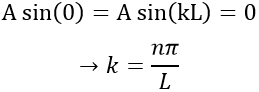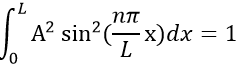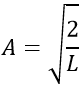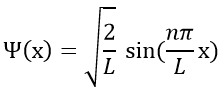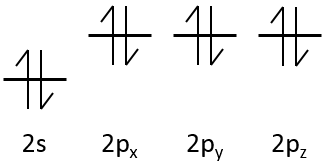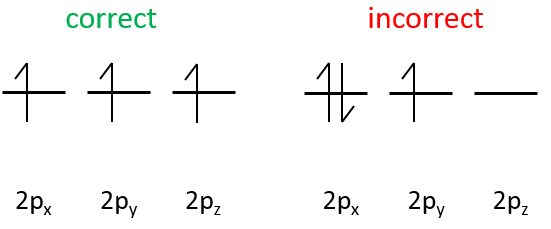Reprenons ce que nous savons des atomes : les atomes peuvent être décomposés et sont composés d’espèces chargées(protons etélectrons) et de particules neutres(les neutrons). Les atomes sont différents pour chaque élément (ou isotope) par le nombre de ces trois espèces. Un noyau est au centre de l’atome et est entouré de vide et d’un nuage d’électrons. Le noyau est constitué de neutrons et de protons et fait la majeure partie de la masse de l’atome. Toutefois la distribution spatiale des électrons est non aléatoire. Plusieurs théories planétaires orbitales ont été proposées après les travaux de Rutherford sur le noyau atomique mais il est le modèle de Bohr qui peut être considéré comme le premier modèle viable. Certaines des hypothèses de ce modèle ne sont pas correctes, mais il a été la première étape vers la compréhension de la structure de l’atome.
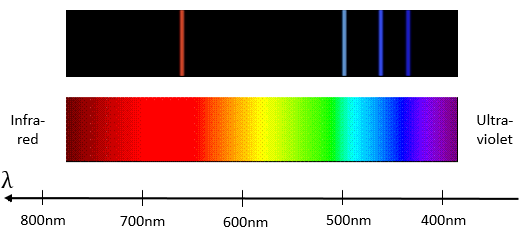
Bohr a travaillé sur l’émission de lumière à partir de dihydrogène H2. Dans un environnement électrique H2 se dissocie en 2 H* excités qui émettent de la lumière avant de retourner à leur état (niveau) fondamental.
hv est la façon habituelle de représenter un photon, émis ou absorbé lors d’un processus physique ou chimique. h=6.626×10−34Js est la constante de Planck. La lumière émise a seulement quelques longueurs d’onde sélectionnées.
Basé sur ce fait, il a élaboré un modèle pour la structure électronique de l’atome. Malheureusement le modèle ne fonctionne que pour l’hydrogène et le cation de He, c-à-d des atomes avec un électron unique.
Bohr a utilisé 4 postulats :
1- les électrons tournent sur des orbitales circulaires
2- sur une orbitale donnée, un électron ne doit pas perdre de l’énergie
3- les gains ou les pertes d’énergie correspondent au saut d’un orbital à l’autre.
4- les électrons sont soumis à un moment angulaire L
Bohr a calculé le rayon et l’énergie des orbitales : pour rester sur une orbitale circulaire donnée l’électron subit une force centrifuge (partie gauche de l’équation) qui est contrebalancée par l’attraction du noyau (partie droite)
où ε0 est la permittivité du milieu. Comme MVR = NH, nous pouvons simplifier les équations comme ce-ci :
En introduisant la force centrifuge dans l’équation précédente, nous obtenons une expression pour le rayon d’un électron :
L’énergie d’un électron est la somme de son énergie cinétique et de son énergie potentielle. L’énergie potentielle vient directement de la force de Coulomb (rappelez-vous que l’énergie est une force multipliée par la distance)
Le rayon a été déterminé précédemment et peut être utilisé pour déterminer l’énergie d’un électron d’un atome donné :
R est la constante de Rydberg et R=-2.178 10-18J.
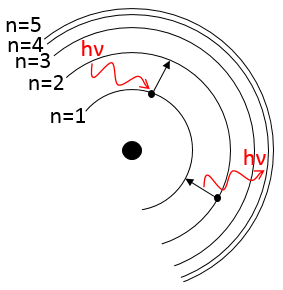
Pour passer à une orbitale du plus grand nombre/rayon, un électron nécessite une quantité d’énergie donnée, obtenue à partir de la chaleur ou de la lumière, ce faisant l’électron est dit excité.
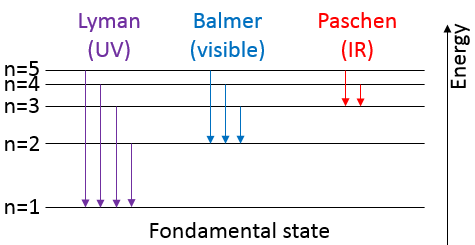
Pour revenir à son état fondamental l’électron excité libère la même énergie sous la forme d’une lumière d’une longueur d’onde donnée. La longueur d’onde de la lumière est directement liée à la différence d’énergie entre les orbitales :
Ce genre de transition à partir d’un niveau excité à la fondamentale est appelé une transition de Lyman et émet dans les longueurs d’onde UV. Si le niveau de destination n’est pas le niveau fondamental, d’autres noms sont donnés :
La deuxième hypothèse de Bohr était incorrecte et les électrons interagissent ensemble.
Pour déterminer la bonne forme de l’orbitale et la position des électrons il est d’abord nécessaire de développer la mécanique quantique.
Mécanique quantique
Un principe important de la mécanique quantique est le principe d’incertitude de Heisenberg : il est impossible de déterminer à la fois la position exacte et le mouvement exact d’une particule comme un électron ou un photon :
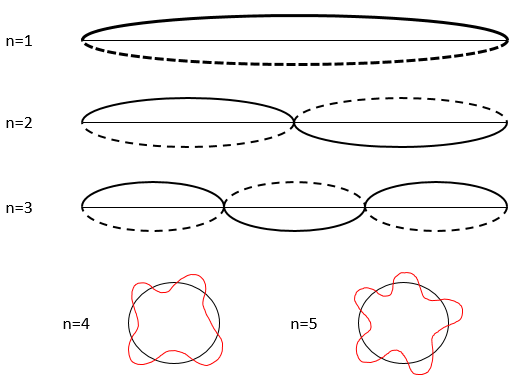
Cette relation signifie que nous pouvons travailler avec probabilité pour estimer la position d’un électron. L’électron n’est pas considéré comme un point mais comme une onde stationnaire le long de son orbite.
La vague a un nombre donné n ( (1, 2, 3, …) des points fixes, à savoir les points où l’onde croise la position théorique de l’électron sur son orbitale. Il est plus facile d’expliquer cela sur une trajectoire linéaire mais il fonctionne aussi bien sur une orbitale circulaire. Ce nombre n sera utile plus tard.
Pour déterminer(la probabilité de) la position d’un électron nous devons résoudre l’équation de Schrödinger
Ĥ est l’opérateur hamiltonien et Ψ est la fonction d’onde à déterminer. Pour résoudre cette équation nous utilisons la particule dans la méthode de la boîte : imaginez une boîte carrée de longueur L contenant une particule, la probabilité de trouver la particule en un lieu donné peut être déterminée. Dans notre cas la particule est un électron et le noyau se trouve dans le centre de la boîte.
Ainsi, la relation à résoudre est :
Le fait que la seconde dérivée de la fonction donne la fonction elle-même implique que celle-ci doit être sinus ou cosinus. Le fait qu’elle est négative indique qu’elle doit être une fonction sinus. Nous allons essayer une solution du type :
A et k seront déterminés plus tard mais ne dépendent pas de x. Nous pouvons maintenant facilement confirmer notre hypothèse précédente :
Comme A ne dépend pas de x, il peut être supprimé sur le dérivé sans problème et de simplifier l’autre côté de l’équation :
Nous donne une relation pour E :
Les valeurs de k et de A seront désormais déterminées à partir des conditions des frontières de la boîte :
– L’électron n’est pas sur les frontières :
– L’électron est dans les frontières de la boîte. Sa probabilité de présence Ψ2
De la première relation nous trouvons la valeur de k :
Compte tenu de cela la deuxième relation donne la valeur de A :
L’intégrale du sinus est égale à 1, par conséquant la valeur de A est simplement
La fonction d’onde est donc :
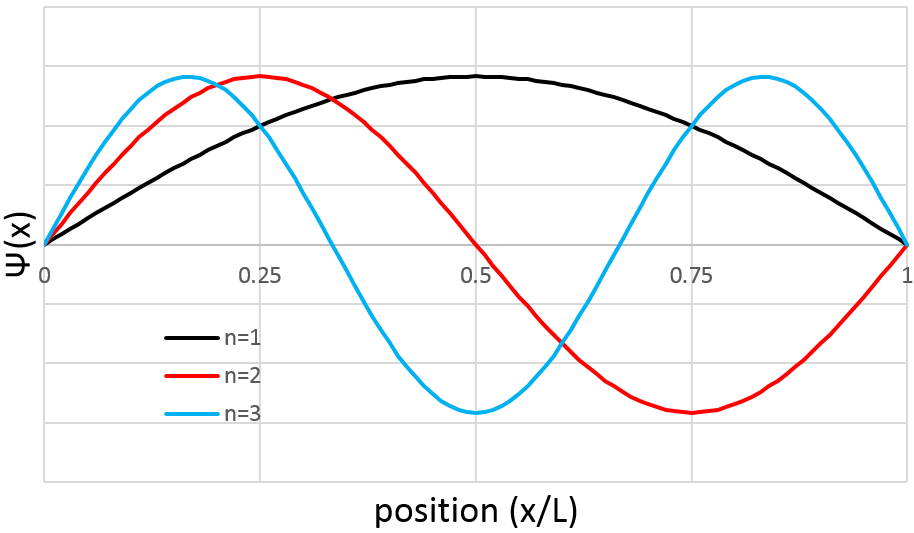
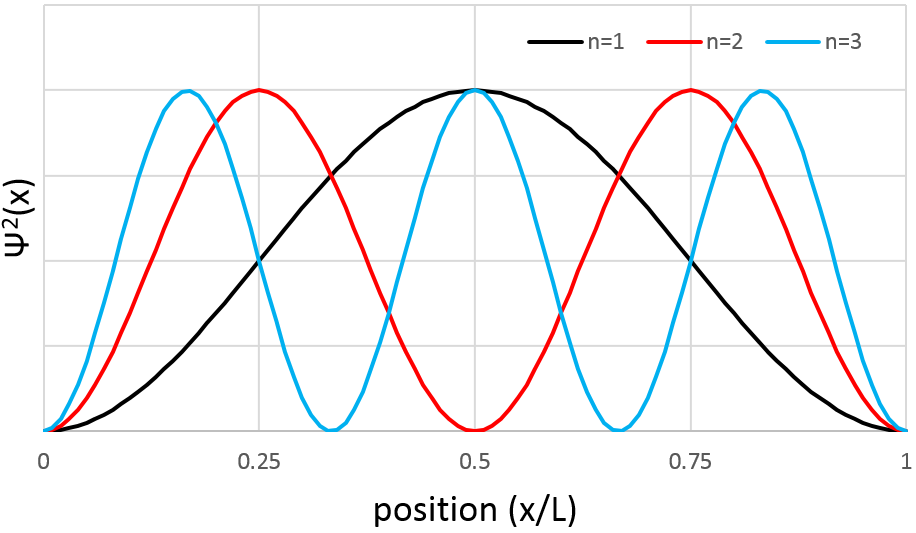
La probabilité de trouver un électron à un endroit donné est Ψ2 (x) :
En conséquence pour n = 1, la probabilité de trouver un électron est le plus grand au centre de la boîte, à savoir près du noyau. Pour n = 2 il ya un point fixe au centre de la boîte, ce qui signifie que la probabilité d’être près du noyau est nulle.
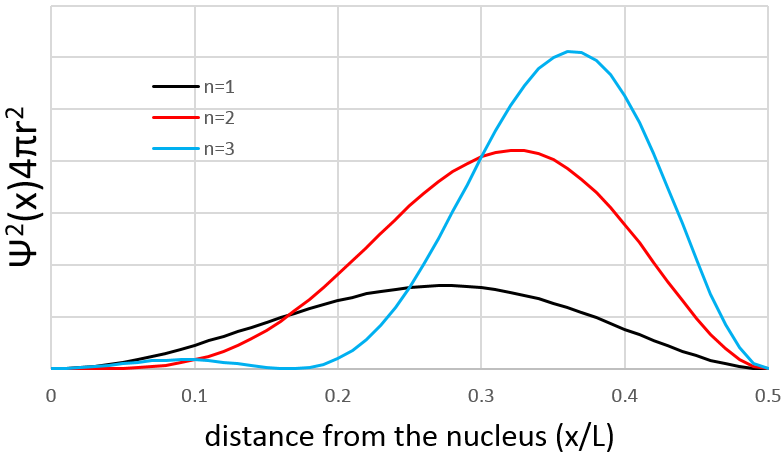
Cependant le volume près du noyau est très limité et ce paramètre doit être pris en compte. Nous utilisons donc une probabilité de présence radiale : Ψ2(x)4πr2 pour obtenir la distribution des électrons.
Selon n la probabilité de la position d’un électron peut donc varier. Pour une augmentation de n la distance des électrons augmente mais deviennent de plus en plus près les uns des autres (rappelez-vous les chiffres du modèle de Bohr).
Nous n’allons pas développer beaucoup plus la mécanique quantique dans cette section. Une autre notion est toutefois nécessaire pour déterminer le nombre d’électrons dans les orbitales différentes : les nombres quantiques.
Nombres quantiques
Il ya 4 nombres quantiques (NQ)
1- NQ principal : n=1, 2, 3,… ce nombre définit la taille et l’énergie de l’orbitale.
2- NQ de moment angulaire : l. L va de 0 à n-1. En fonction de la valeur de l, les orbitales sont nommées s, p, d ou f. Les formes de ces orbitales sont différentes
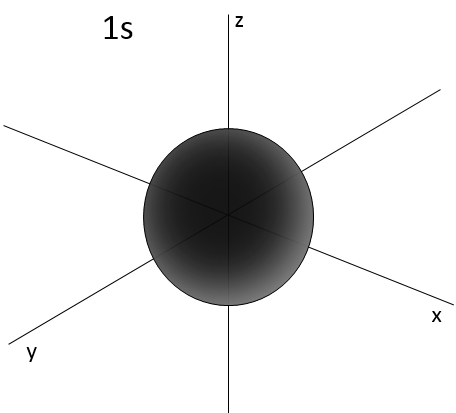
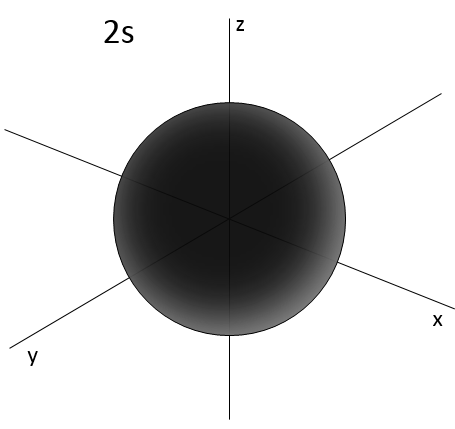
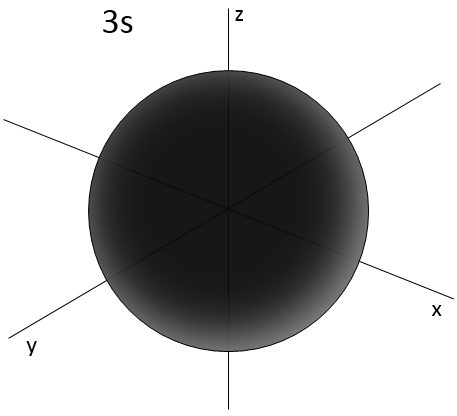
- Orbital s
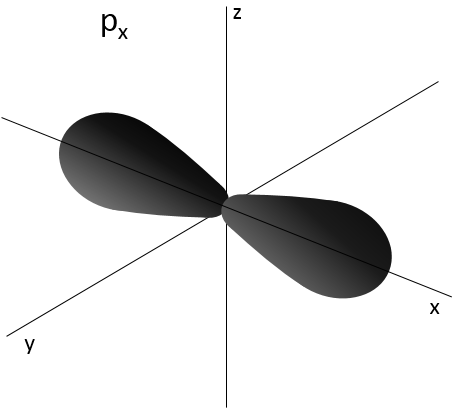
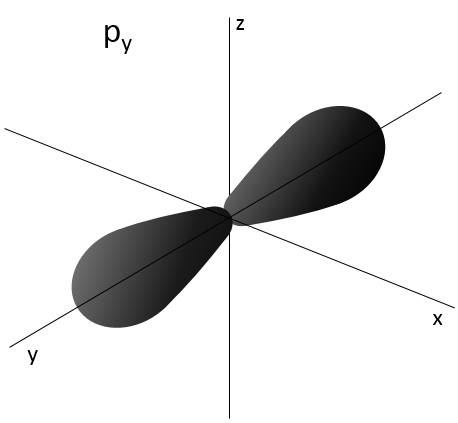
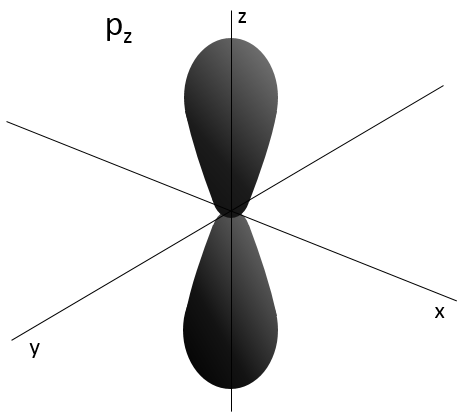
- Orbital p
Les orbitales p sont axiales
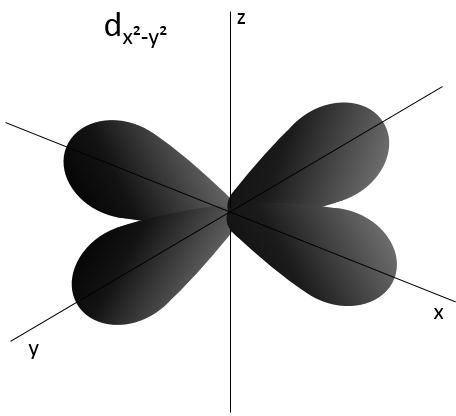
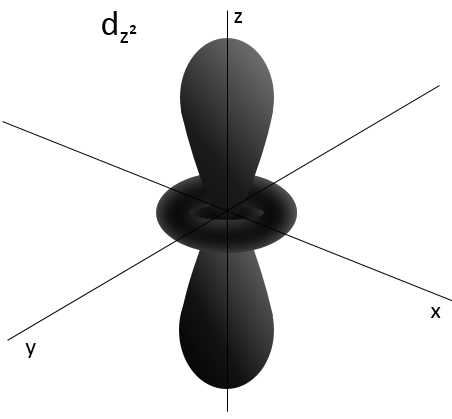
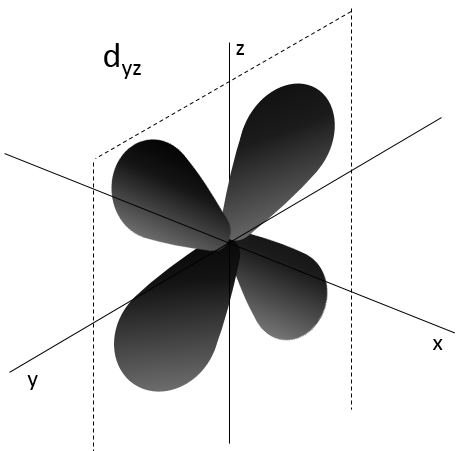
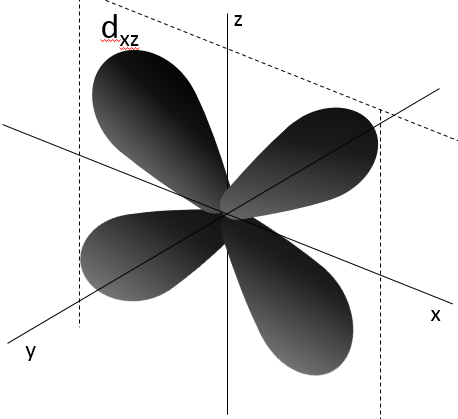
- Orbital d
Les orbitales d sont essentiallement biaxiales. Deux sont sur les axes et les 3 autres sontà 45° entre les axes.
- Orbital f
Les Orbitales f sont polyaxiales (nous n’allons pas les dessiner ici)
3- NQ magnétique : ml
ml passe de -l à l et définit l’orientation de l’orbitale
4- NQ du spin : ms
ms définit le spin des électrons. Les électrons peuvent aller dans deux directions opposées et ms = -½ ou ½.
Les électrons doivent avoir un ensemble différent de NQ : c’est le principe de l’exclusion de Pauli. Cela signifie qu’une orbitale ne peut accepter qu’un nombre donné d’électrons. On peut donc seulement avoir deux électrons de spins opposés pour un ensemble de trois autres NQ. Lorsque les deux électrons sont ensemble on dit qu’ ils sont jumelés.
Par exemple il peut y avoir 8 électrons pour n = 2 : l peut avoir une valeur de 0 ou 1
Pour l = 0 l’orbitale correspondant est l’orbitale 2s. ml = 0 et ms peut être soit ½ ou -½. Il ya donc deux électrons de spins opposés dans l’orbitale 2s.
Pour l = 1, l’orbitale correspondante est 2p. Trois valeurs de ml sont possibles (allant de -l à l) : ml = -1, ml= 0 et ml= 1 (correspondant aux trois directions cartésiennes x, y et z). Chacune de celles-ci peut accepter un électron du spin ½ et -½. L’orbitale 2p peut donc posséder 6 électrons.
Au total, 8 électrons peuvent être placés pour n = 2
Si n = 3, 10 électrons supplémentaires peuvent être placés dans l’orbitale d pour un total de 18.
Toutes les orbitales ne possèdent pas la même énergie et les électrons vont d’abord prendre place dans les orbitales d’énergie plus faible. En effet les électrons externes sont sur orbitales plus énergiques : les couches intérieures d’électrons ont un effet de blindage sur la charge du noyau et ont également un effet de répulsion sur les électrons externes.
L’énergie de l’orbitale dépend de n :
E (n = 1) <E (n = 2) <….
Mais aussi de l
Ens<Enp<End<Enf
Toutefois le classement global est plus compliqué que seulement toutes les orbitales de n = 1, puis n = 2, etc …
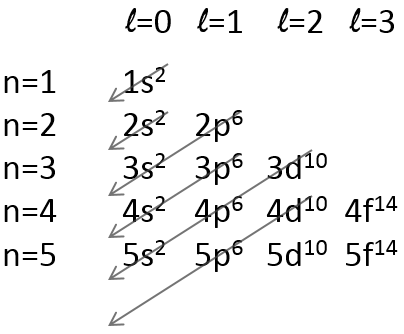
Il existe une méthode pour se rappeler l’ordre dans lequel nous plaçons les électrons sur les orbitales :
Les électrons sont placés suivant les flèches. 2 électrons peuvent être placés sur orbitales ns, 6 sur orbitales np, 10 sur orbitales nd et 14 sur orbitales nf. Ce numéro est indiqué sur la figure en haut à droite pour chaque ensemble (n, l) de l’orbitale. Deux électrons sont d’abord placés sur l’orbitale ls chacune avec un spin différent. On fait de même dans l’orbitale 2s. Il faut moins d’énergie pour placer deux électrons appariés sur l’orbitale ls que l’un dans l’orbitale 1s et un dans l’orbitale 2s . Cependant dans un même ensemble de (N, L), il faut moins d’énergie pour placer un électron sur chaque orbitale. Donc il ya trois orbitales dans le 2p : 2px, 2py et 2pz. Un électron est ainsi placé sur chacun de ces trois orbitales puis les électrons sont jumelés.
Il y a quelques exceptions à cette méthode en raison de la stabilité notamment des orbitales d. Les orbitales d sont les orbitales externes des atomes métalliques de transition, elles sont très stables quand elles sont complètes ou demi-complètes, c.à.d quand elles ont 10 ou 5 électrons. Les électrons des orbitales inférieures peuvent être déplacés dans les orbitales d pour atteindre ce quota. Jetons un coup d’oeil sur certains métaux afin de mieux comprendre ce phénomène.
La configuration électronique de V (Z = 23) est :
[Ar] 4s2 3d3
On n’a pas besoin d’écrire la configuration complète d’atomes. Les électrons internes ne disposent pas d’incidence sur les propriétés de l’atome. Au lieu de cela, nous écrivons le nom du gaz noble précédent entre accolades. Argon (Ar) a Z = 18 donc il y a encore 5 électrons à placer sur les orbitales. Les 2 premiers électrons sont jumelés sur les 4s et les trois autres sont placés sur 3 orbitales 3d. Même si 4s dispose d’un plus grand n, il est moins énergique que 3d en raison d’un effet de pénétration (développer). Il n’ y a rien de particulier dans ce cas.
La configuration électronique de Cr (Z = 24) qui a plus d’électrons que V est :
[Ar] 4s1 3d5
Un électron a été pris à partir des orbitales 4s pour atteindre le demi achèvement des orbitales d. Pour Z = 25 (Manganèse, Mn), l’orbitale 4s reçoit l’électron supplémentaire. Le même phénomène se produit pour le cuivre Cu (Z = 29) pour obtenir une orbitale complète 3d :
Ni: [Ar] 4s2 3d8
Cu: [Ar] 4s1 3d10
Sur la table périodique de Mendeleïev une ligne commence lorsque nous plaçons un premier électron dans une orbitale ns. Cependant, ce n’ est pas de cette façon que le tableau a été élaboré initialement. Nous allons examiner de près ce tableau dans le chapitre suivant, expliquant sa forme, les éléments et les propriétés générales qui peuvent être directement liées à la place de l’élément dans le tableau.