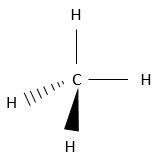
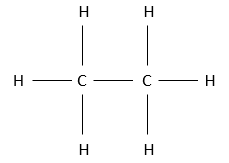
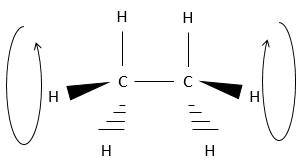
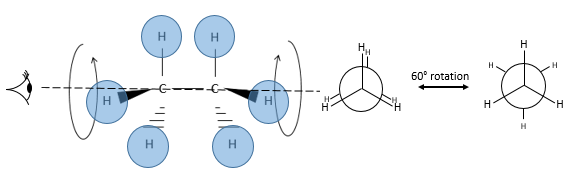
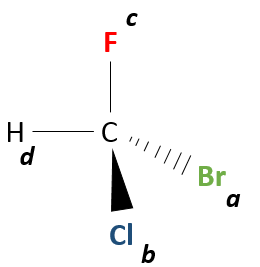
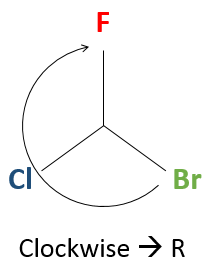
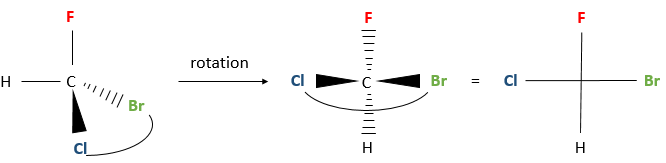
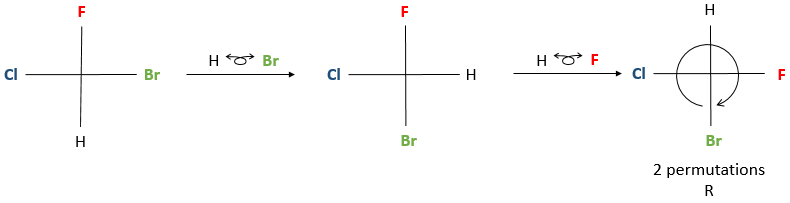
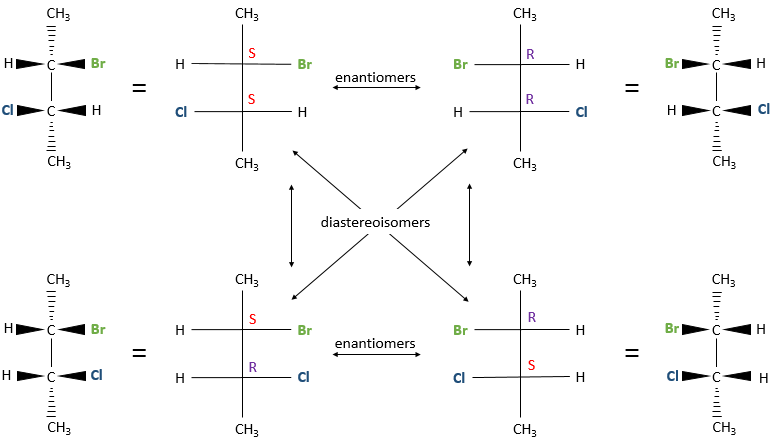
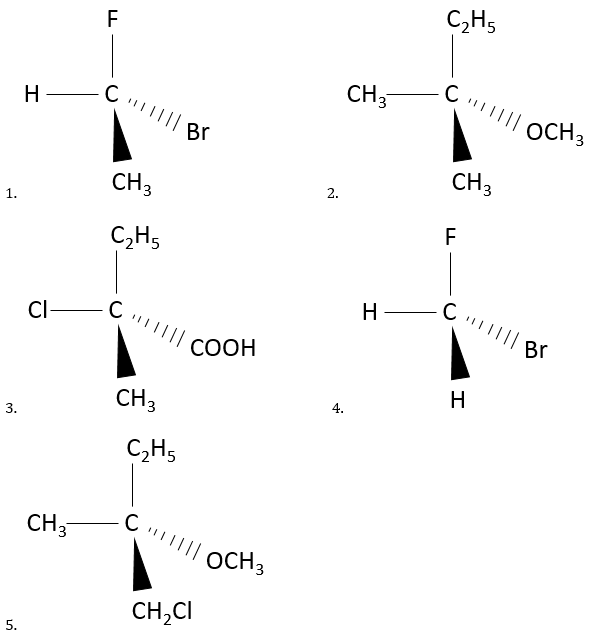
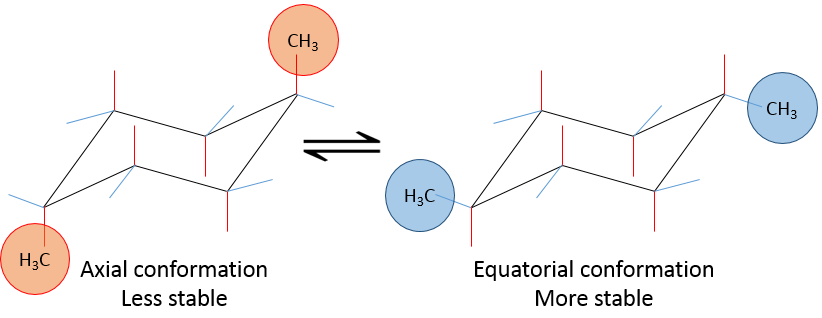
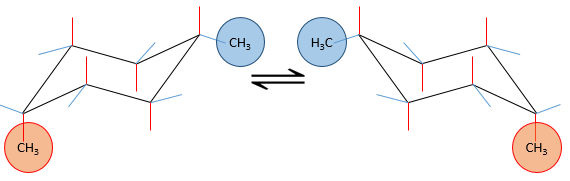
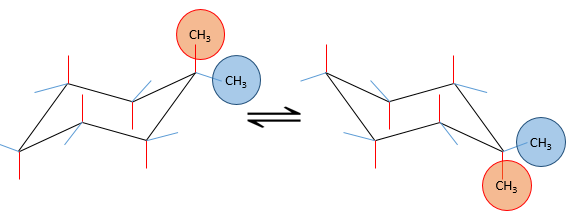
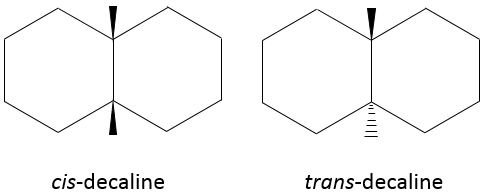
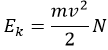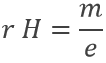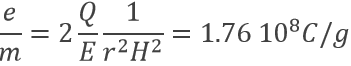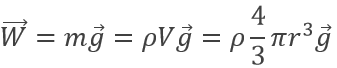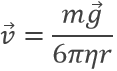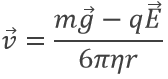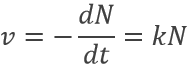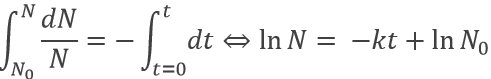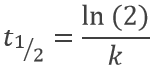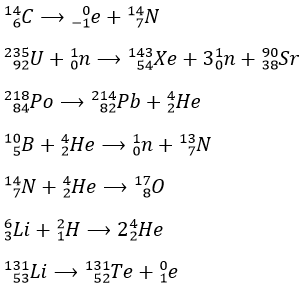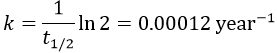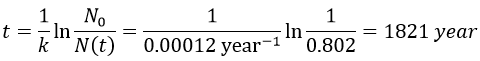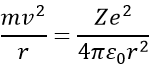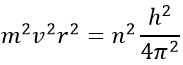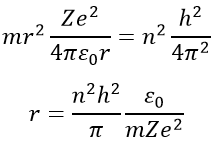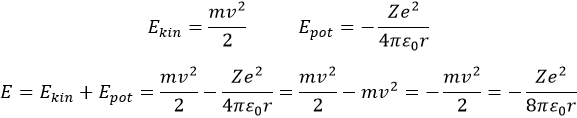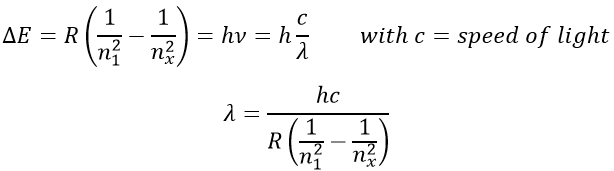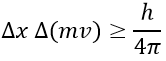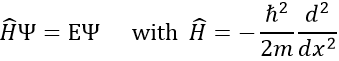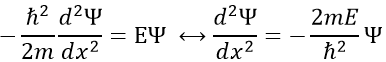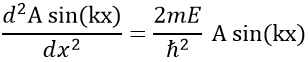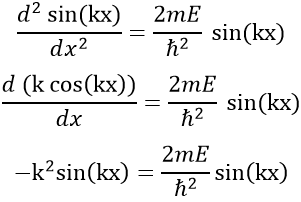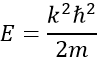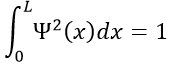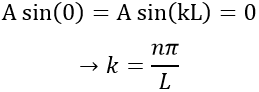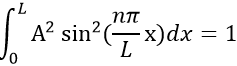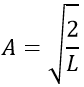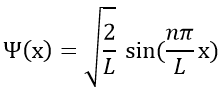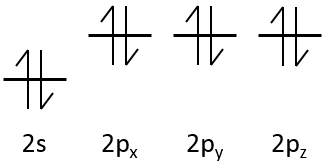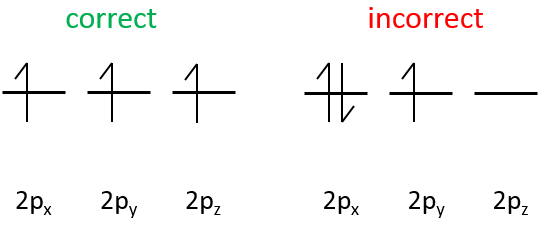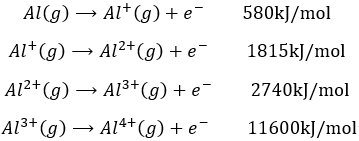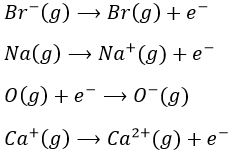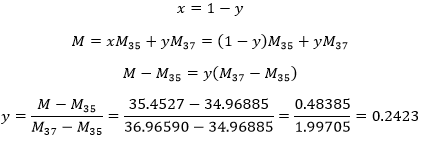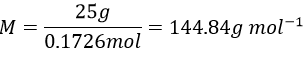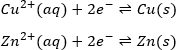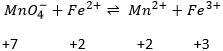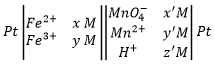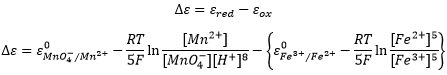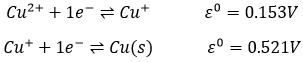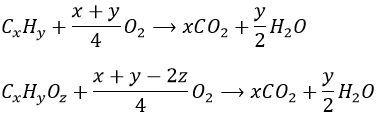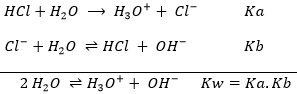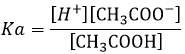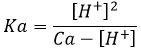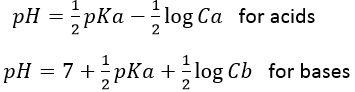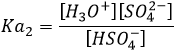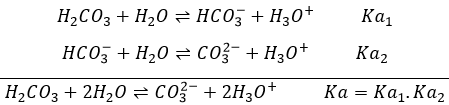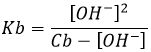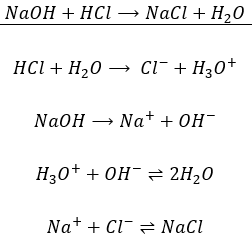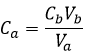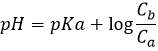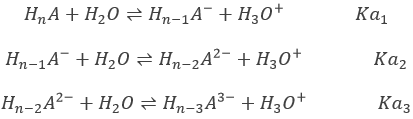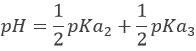Chapter 1b: Atomic theory and nuclear reactions
Atomic theory
At the end of the XIX, it was known that the elements were made of one atom, unbreakable and different for each element. The masses of the atoms were known for several elements but their composition was still a mystery.
Michaël Faraday discovered that atoms were in fact composed of charged species, even if they are electrically neutral. His discovery was the result of an experiment in which a current passes through silver electrodes sunk in a solution containing silver (AgNO3). When the current passes, the mass of the electrode increased significantly. The silver ions in the solutions reacted with the electrons from the current to form solid silver gathering on the electrode.
This reaction showed that atoms contain positively charged elements, and therefore negatively charged species to neutralise the charge of the atom.
Joshep John Thompson proved the existence of electrons in 1897 during his works on cathodic tubes. Those tubes only contain void, a cathode and an anode. If the cathode is heated, a current is detected between the electrodes. The heating determines the kinetic energy transmitted to the atom of the cathode:
While the charge e of the electrons is given by the current:
Applying a magnetic field H on the cathodic tube, if only a small gap allowed electrons to reach the anode, no current was observed: the electron beam deviates from its normal trajectory depending on the ratio mass/charge. The walls of the gap were covered by ZnS, a fluorescent species to detect the deflection of the beam (radius of deflection r):
As a result, the ratio e/m of an electron was determined:
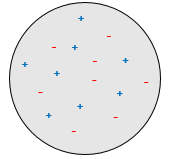
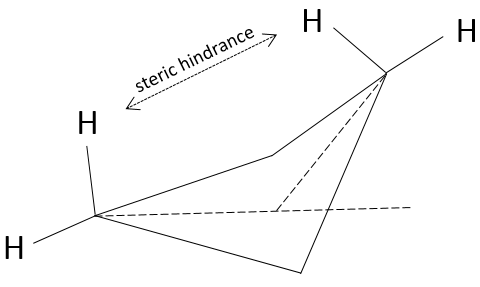
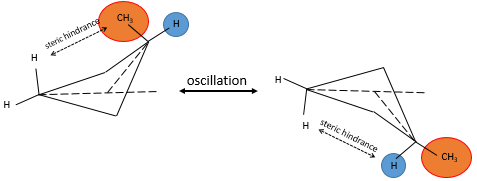
J.J. Thompson imagined a model of a spherical atom wherein a sea of charged species are moving (the plum pudding model).
The charge of the electron was determined by Robert Andrews Millikan. He beamed RX on droplets of oil between two horizontal electrodes. The charged droplets are subjected to several forces: their own weight, the electrostatic force and the friction of the air (air has a given viscosity).
The weight of a droplet is given by
m being the mass of a given droplet, equal to its density multiplied by its volume, and g is the gravity. The electrostatic force is given by
where E is the electric field and q is the charge. The friction is given by
where η is the air viscosity and v is the speed of the droplet. In absence of electric field, the droplet should fall at a speed
resulting from the equations of W and FR. However in the electric field E, the speed of a droplet is affected:
Except q, all the terms of the right side of the equation are known and the speed of droplets was experimentally determined: a droplet is observed through a microscope to measure the time it takes to travel a given distance.
The result of the experiment was that the charge q was always a multiple of 1.602 10-19C, some droplets being several times charged.
The mass of an electron could thus be determined as well: me=9.11 10-31kg.
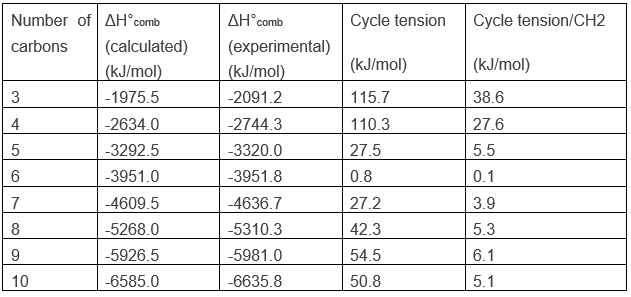
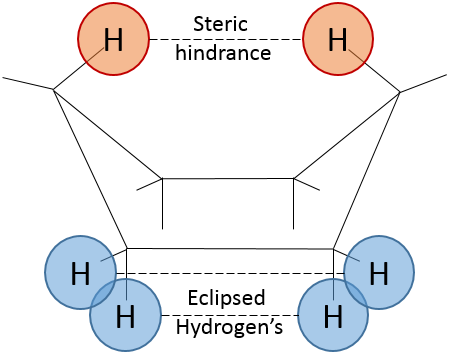
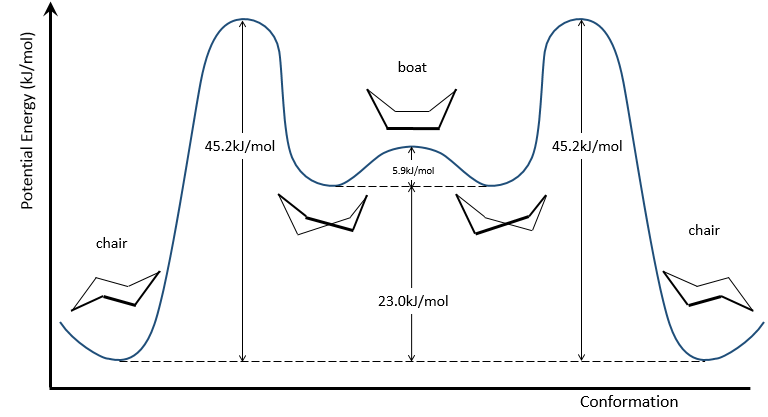
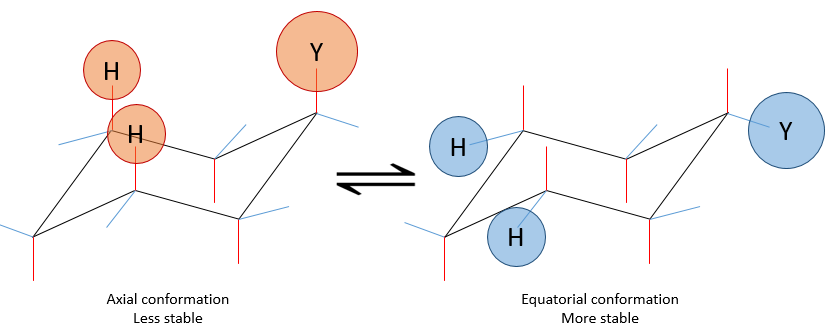
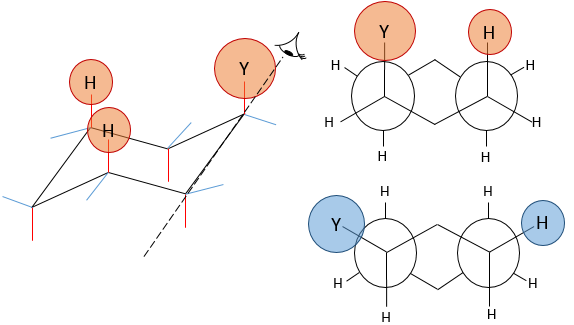
Despite his brilliant experiment, the plum pudding model of J.J Thompson was not correct and got refuted by Ernest Rutherford (who actually has been one of his student), the pioneer of the nuclear chemistry. Rutherford studied the emission of α particles from Uranium. α particles are the equivalent of the nucleus of Helium atoms: 2 neutrons and 2 protons: He2+. α particles were beamed towards a thin foil of gold. Considering the model of Thompson, all of the radiation should have passed through the gold foil. 99% of it passed, and it was not due to an experimental error. Some of the α particles were deflected in all directions. He concluded that the 1% deflected on a solid aggregation with an intense positive charge and composing the majority of the mass of the element. The rest of the volume of an atom being filled by empty space and a cloud of electrons. The size of an atom is about 1 angström (1Å)=10-10m of diameter and the size of a nucleus is 10-15m.
Rutherford was also the first to transmute an element into another one. He did that by bombarding pure nitrogen by α particles and obtained oxygen and hydrogen nuclei (protons were not yet known). He assumed that hydrogen nuclei are part of the solid nucleus of the atoms. From now, atoms were no more unbreakable.
Later, Rutherford theorized the existence of neutrons to keep the positively charged nucleus in one piece, reducing the repelling of protons and giving a cohesion energy to the nucleus. The bigger the atom, the more neutrons are needed (in proportion with protons).
This energy of cohesion is actually enormous. For example Oxygen is made of 8 neutrons and 8 protons. But the mass of the atom of oxygen is smaller than the addition of the mass of the separated protons and neutrons:
The mass of an oxygen atom is 2.65535.10-23g. The difference is about 2.269.10-25g by atom. As E=mc2, we obtain for one mole an energy of cohesion of 1.23.1013J/mol of oxygen. For comparison, a typical chemical reaction is ~105J/mol. There is thus no surprise why nuclear reactions car produce so much energy.
Nuclear reactions
Nuclear chemistry is a very specific domain of chemistry. It is one domain where the Lavoisier rule does not apply: the elements are not conserved and mass can be converted into energy. Yet, several types of reactions can be sorted. But first, we will take a look at how to write the isotopes involved. We have seen that each chemical elements is an atom with a specific composition of protons, electrons and neutrons. This composition gives the sepcific properties of each element. However, there can be several forms for many elements. Those forms are the isotopes. They differ by their number of neutrons, the number of electrons and of protons being equal and fixed for every element. The chemical properties of isotopes are almost identical (because given by the electrons), but some physical properties can be different between isotopes of the same element. The speed of reaction and the ebullition temperature are two examples of properties that change depending of the isotope. The isotope 238 of Uranium is written
U is the symbol of the element, the mass is written at the top left of the element and its atomic number Z is written at the bottom left. The atomic number can be skipped. The proportions the isotopes of a single element are not equal. For instance, the carbon has 2 stable isotopes: 12C and 13C with a proportion of 98.93% and 1.07%. 14C is an isotope of the carbon but it is not stable: it decays over time. Historians use this property to date ancient items or bodies.
- Production of α particles
Remember that an
The decay of Uranium 238 is an example of reaction producing α particles:
The total value of the top number is conserved during the reaction. The same is true for the bottom number. The γ product is gamma radiation, produced by radioactive decays because the formed nucleus is generally in an exited mode. To come back to its base state, energy is thus freed in the form of an electromagnetic radiation
- Production of β particles
The β particles are small charged species emitted during some nuclear reactions. The Thorium 234 obtained previously can produce this kind of particles
The mass of the element did not change during this reaction. However, the element changed from Thorium to Protactinium. One neutron became a proton. The β particles produced during this reaction is an electron rejected from the neutron to become a proton.
An antineutrino is also generated. A nucleus has a given spin depending on its charge: it turns on itself in a given direction. Electrons also have a spin. During the nuclear reaction from above, the charge of the nucleus changed and an antineutrino is liberated to obtain the correct spin.
A second β particle can be obtained, for example during the decay of Sodium 22
The β particle is not an electron but a positron. A neutrino is also obtained during this reaction. Neutrinos and antineutrinos are radiations that can go through everything.
Electrons and positrons can neutralize to produce a gamma radiation
- Fission
Fission is done by bombarding an isotope with neutrons. In nuclear plants, fission is done on Uranium 235
There is more neutrons produced by the reaction than needed to launch it. This reaction can thus start again as long as there is Uranium 235 in the reactor. Another way to stop the reaction is to trap the neutrons with another isotope.
- Fusion
Fusion is done by merging two isotopes. For example, two isotopes of Hydrogen can produce Helium
![]()
Another way to obtain Helium is to bombard Hydrogen with electrons.
It is also a fusion reaction.
The elements used in fusion and in fission are different. The energy of cohesion is different for each element and we can observe a maximum of energy of cohesion/nucleon (proton+neutron) for 56Fe. Fusion is performed on elements of lower mass up to the 56Fe. Atoms gain energy of cohesion during fusion. On the other side, elements of higher mass lose cohesion energy and mass up to the 56Fe.
Half-life time
Radioactive elements do not stay active forever. The radioactivity decreases over time proportionally at the number or particles.
where v is the speed of decomposition, N the number of radioactive particles and k is a speed constant depending on the isotope.
Because it depends on the number of particles, the speed decreases over time. We can integer the speed equation
The half-life time is the time needed to decrease the population of a radioactive element by half:
This time does only depend on the isotope and does not depend on the population of the isotope.
Exercises
1. Complete these nuclear reactions:
2. A piece of manuscript has been analysed for dating. It has been found that the ratio 14C/12C of the manuscript is equal to 0.802 times the value of a plant of today. Given that the half-life time of 14C is 5720years, what is the age of the manuscript?
3. How much energy is generated by the fusion of 1.2g of deuterium (D or 21H)
given that the masses of the two species are MD=2.0141g/mol and MHe=4.0026g/mol?
Answers
1.
2. The half-life time of a radioactive element defines the time it takes to the element to decrease its population by half. The general formula to calculate the population of an isotope is
The half-life time is
It allows us to determine the value of k:
The ratio 14C/12C that we have in the wording is the reverse of N0/N(t). Now that we know the value of k, we can thus find the age of the manuscripts with the equation
3. In 1.2g of deuterium, there is 1.2g/2.0141g/mol=0.5958mol. We need two deuterium to form one atom of helium, so the amount of helium after the reaction is 0.2979mol.
The energy ΔE generated by the reaction is proportional to the mass Δm lost during the reaction. This mass lost for each produced mole of He is
Thus Δm=0.007626g for 1.2g of deuterium. The energy generated is given by
Chapter 1c: Electronic structure of atoms
Let’s resume what we know from the atoms: atoms can be broken and are composed of charged species – protons and electrons – and neutral particles – the neutrons. Atoms are different for each element (or isotope) by the number of those three species. A nucleus is at the centre of the atom and is surrounded by void and a cloud of electrons. The nucleus is made of neutrons and protons and makes the major part of the mass of the atom. However, the spatial distribution of the electrons is not random. Several planetary orbit theories were proposed after the works of Rutherford on the atomic nucleus but it is the Bohr’s model which can be considered as the first viable model. Some of the hypotheses of this model were not correct but it was the first step toward the understanding of the structure of an atom.
Bohr worked on the emission of light from dihydrogen H2. In an electric environment H2 dissociates in 2 excited H* that emit light to get back to its fundamental level.
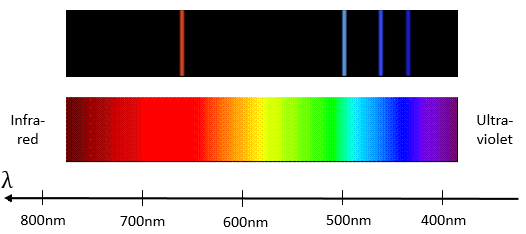
hν is the usual way to represent a photon, emitted or absorbed during a physical or chemical process. h=6.626×10−34Js is the Planck constant. The emitted light has only a few selected wavelengths.
Based on that fact, he elaborated a model for the electronic structure of the atom. Unfortunately, the model only works for the Hydrogen and for the cation of He, i.e. atoms with a single electron.
Bohr used 4 postulates:
- electrons revolve on circular orbitals
- On a given orbital, an electron does not lose energy
- Gains or losses of energy correspond to the jump from one orbital to another one.
- Electrons are subject to a angular moment L
Bohr calculated the radius and the energy of the orbitals: to stay on a given circular orbital, the electron endures a centrifugal force (left part of the equation), which is counterbalanced by the attraction of the nucleus (right part)
where ε0 is the permittivity of the medium. As mvr=nħ, we can simplify the equations from the square of it:
Injecting the centrifugal force into the previous equation, we obtain an expression for the radius of an electron:
The energy of an electron is the sum of its kinetic energy and its potential energy. The potential energy comes directly from the Coulomb’s Force (remember that an energy is a force multiplied by a distance)
The radius was determined previously and can be used to determine the energy of an electron for a given atom
R is the constant of Rydberg and R=-2.178 10-18J.
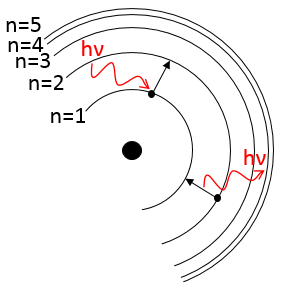
To jump to an orbital of greater number/radius, an electron requires a given amount of energy, obtained from heat or light. Doing so, the electron is said excited.
To go back to its fundamental state, the excited electron frees the same energy in the form of a light of a given wavelength. The wavelength of the light is directly related to the difference of energy between the orbitals:
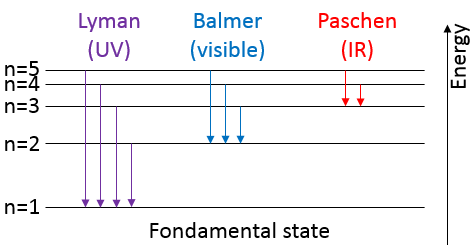
This kind of transition, from an excited level to the fundamental one is called a Lyman transition and emits in the UV wavelengths. If the destination level is not the fundamental one, others names are given:
The second hypothesis of Bohr was incorrect and electrons interact together.
To determine the correct form of orbital and the position of electrons, it is first necessary to develop quantum mechanics.
Quantum mechanics
An important principle of the quantum mechanics is the uncertainty principle of Heisenberg: it is impossible to determine at the same time the exact position and the exact movement of a particle such as an electron or a photon:
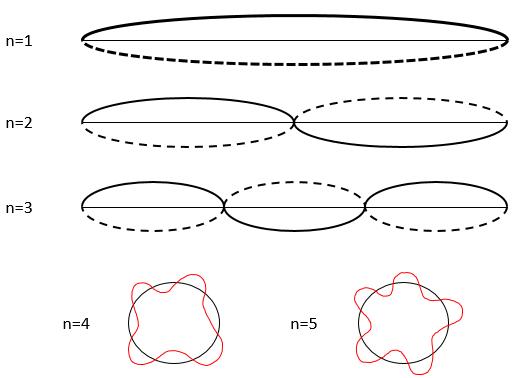
This relation means that we can only work with probabilities for an electron to be at a position. The electron is not considered as a point but as a stationary wave along its orbital.
The wave has a given number n (1, 2, 3,…) of fixed points, i.e. points where the wave crosses the theoretical position of the electron on its orbital. It is easier to explain this on a linear path but it works as well on a circular orbital. This number n will be useful later.
To determine the (probability of) position of an electron, we have to solve the equation of Schrödinger
Ĥ is the Hamiltonian operator and Ψ is the wave function, to be determined. To solve this equation, we use the particle in the box method: considering a square box of length L containing a particle, the probability to find the particle at a given place can be determined. In our case, the particle is an electron and the nucleus is in the centre of the box.
So, the relation to solve is
The fact that the second derivative of the function gives the function let us guess a sine or cosine function. The fact that it is negative indicates that it is a sine function. We will try a solution of the type
A and k will be determined later but do not depend on x. We can easily confirm our previous guess now:
As A does not depend on x, it can be placed out of the derivative without problem, and simplified with the other side of the equation
Giving us a relation for E
The values of k and of A will now be determined from the boundaries conditions of the box:
- The electron is not on the boundaries
- The electron is in the box. Its probability of presence Ψ2
From the first relation, we find the value of k:
Taking this into account, the second relation gives the value of A:
The integral of the sine equals 1, so the value of A is simply
The wave function is thus
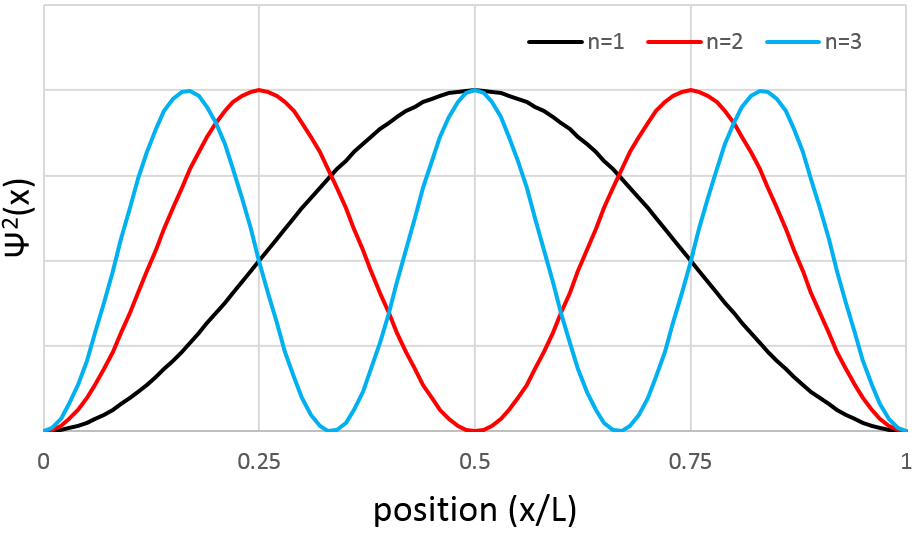
The probability to find an electron at a given place is Ψ2(x):
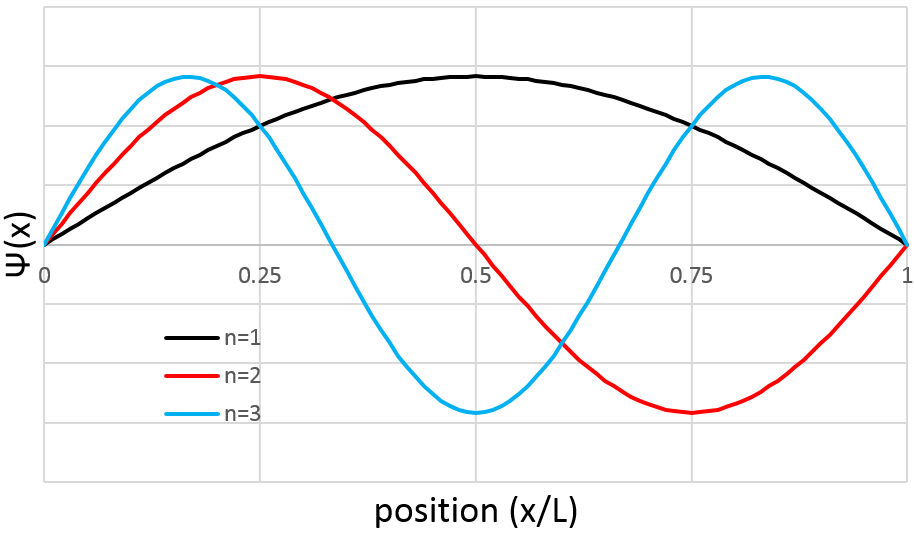
As a result, for n=1, the probability to find an electron is the greatest at the centre of the box, i.e. close to the nucleus. For n=2, there is a fixed point at the centre of the box, meaning that the probability to be near the nucleus is null.
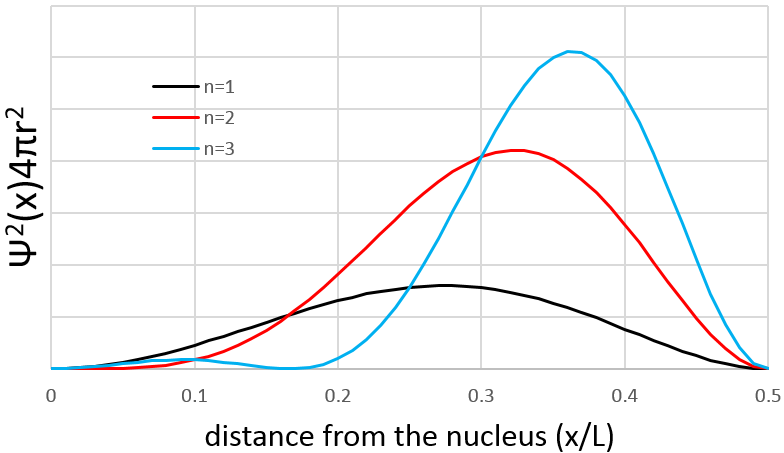
However, the volume near the nucleus is very limited and this parameter has to be taken in account. We use thus a radial probability of presence: Ψ2(x)4πr2 to obtain the distribution of electrons.
Depending on n, the (probability of) position of an electron can thus vary. For an increased n, the distance of the electrons increases but become closer and closer to each other (remember the figures of the Bohr model).
We won’t develop much more develop quantum mechanics in this section. One more notion is however needed to determine the number of electrons in the different orbitals: the quantum numbers.
Quantum numbers
There are 4 quantum numbers (QN)
- Principal QN: n=1, 2, 3,… this number defines the size and the energy of the orbital
- QN of angular moment: l.
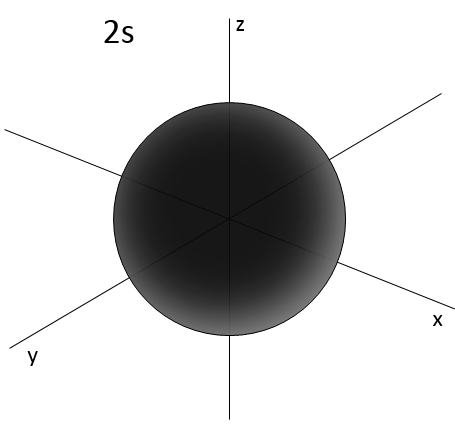
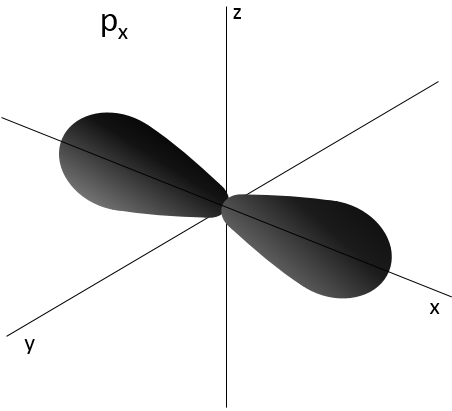
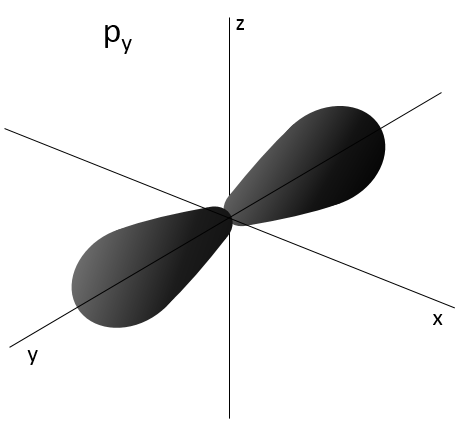
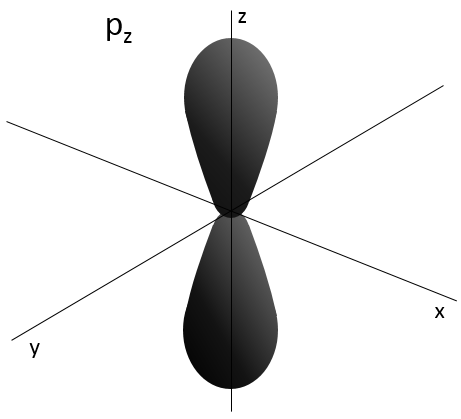
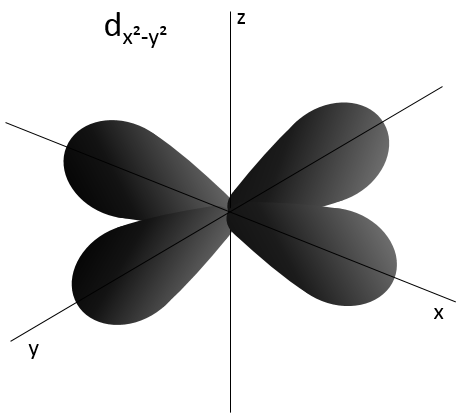
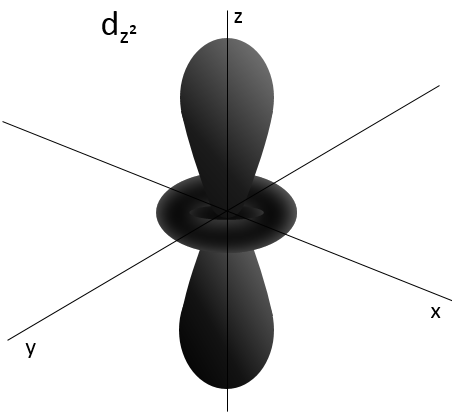
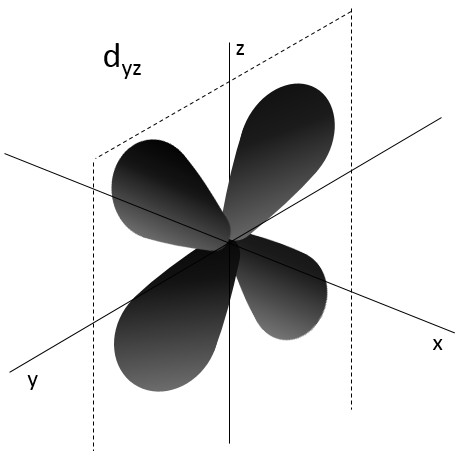
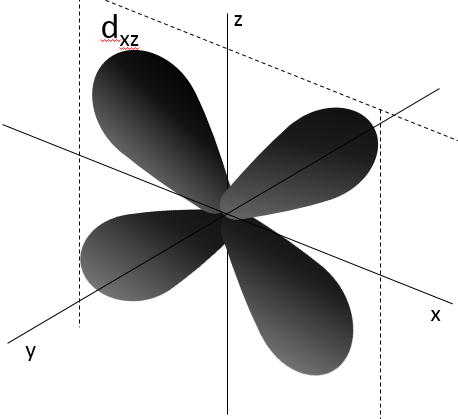
L goes from 0 to n-1. Depending on the value of l, the orbitals are named s, p, d or f. The shapes of these orbitals are different:
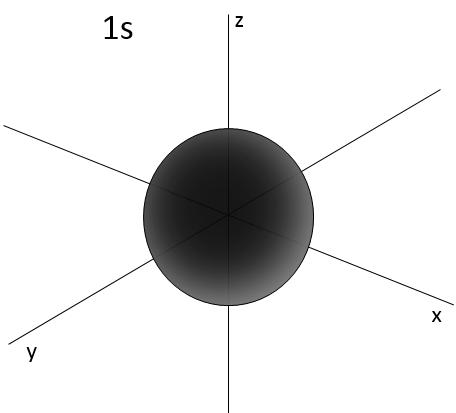
- Orbital s
- Orbital p
Orbitals p are axial
- Orbital d
Orbital d are essentially biaxial. Two of them are on the axes and the three other are at 45° between axes
- Orbital f
Orbital f are polyaxial (and won’t be drawn here, sorry)
- Magnetic QN:ml
ml goes from –l to l and defines the orientation of the orbital
- QN of spin: ms
ms defines the spin of the electrons. Electrons can go in two opposite directions and ms= -½ or ½.
Electrons must have a different set of QN: it is the Pauli’s principle of exclusion. That means that an orbital can only accept a given number of electrons. There can thus only be 2 electrons of opposite spin for a given set of the three other QN. When the two electrons are together, we said that they are paired.
For example, there can be 8 electrons for n=2: l can have a value of 0 or 1
For l=0, the corresponding orbital is the orbital 2s. ml=0 and ms can either be ½ or -½. There are thus 2 electrons of opposite spin in the 2s orbital.
For l=1, the corresponding orbital is 2p. Three ml values are possible (going from –l to l): ml=-1, ml=0 and ml=1 (corresponding in the three Cartesian directions x, y and z). Each of those can accept an electron of spin ½ and -½. The orbital 2p can thus possess 6 electrons.
In total, 8 electrons can be placed for n=2.
If n=3, 10 additional electrons can be placed in the d orbital, for a total of 18.
All the orbitals don’t have the same energy. And electrons will first take place in the lower energy orbitals. Indeed, the external electrons are on more energetic orbitals: the inner sheets of electrons are shielding the charge of the nucleus and also have a repulsion effect on the external electrons.
The energy of orbital depends on n
E(n=1)<E(n=2)<….
But also on l
Ens<Enp<End<Enf
However, the global classification is more complicated than just all the orbitals of n=1, then of n=2, etc…
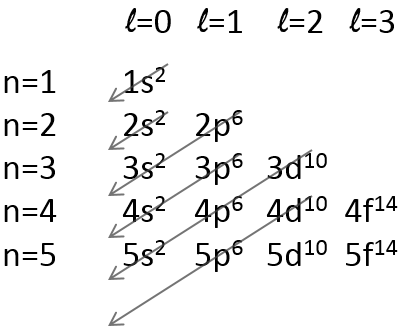
There is a method to remember the order in which we place the electrons on orbitals:
The electrons are placed following the arrows. 2 electrons can be placed on ns orbitals, 6 on np orbitals, 10 on nd orbitals and 14 on nf orbitals. This number is indicated on the figure on the top right for each set (n,l) of orbital. Two electrons are first placed on the 1s orbital, each with a different spin. The same is done in the orbital 2s. It takes less energy to place two paired electrons on the orbital 1s than one in the 1s and 2s orbitals. However in a same set of (n,l) it takes less energy to place one electron on each individual orbital. So, there are three orbitals in the 2p: 2px, 2py and 2pz. One electron is thus placed on each of those three orbitals and then electrons are paired.
There are some exceptions in this method due to the particular stability of d orbitals. d orbitals are the outer orbitals of the metallic atoms of transition. The d orbitals are very stable when they are complete or half complete, i.e. have 10 or 5 electrons. Electrons of lower orbitals can be displaced in the d orbitals to reach this quota. Let’s take a look on some metals to understand better this phenomenon.
The electronic configuration of V (Z=23) is
[Ar] 4s2 3d3
There is no need to write the complete configuration of atoms. The inner electrons don’t have any impact on the properties of the atom. Instead, we write the name of the previous noble gas between accolades. Argon (Ar) has Z=18 so there are still 5 electrons to place on orbitals. The first tow electrons are paired on the 4s and the three other are placed on 3 3d orbitals. Even if 4s has a bigger n, it is less energetic than 3d because of an effect of penetration (develop). There is nothing particular in this case.
The electronic configuration of Cr (Z=24), that has 1 more electron than V is
[Ar] 4s1 3d5
One electron has been taken from the 4s orbital to reach the half completion of the d orbitals. For Z=25 (Manganese, Mn), the 4s orbital receives the additional electron. The same phenomenon occurs for the copper Cu (Z=29) to obtain a complete 3d orbital:
Ni: [Ar] 4s2 3d8
Cu: [Ar] 4s1 3d10
On the periodic table of Mendeleev, a line begins when we place a first electron in a ns orbital. However, this is not this way that the table was developed initially. We will look closely at this table in the next chapter, explaining its shape, the elements and the general properties that can directly be related to the place of the element in the table.
Exercises
1. To which element corresponds this electronic structure:
1s2 2s2 2p4
[Ar] 4s2 3d6
[Ne] 3s1
2. What is the electronic configuration of Ar, Si, Cr, Nb, Al, F, Rb, Es?
Answers
1.
1s2 2s2 2p4 oxygen
[Ar] 4s2 3d6 Fe
[Ne] 3s1 Na
2.
Ar: [Ne] 3s2 3p6
Si: [Ne] 3s2 3p2
Cr: [Ar] 4s1 3d5
Nb: [Kr] 5s2 4d3
Al: [Ne] 3s2 3p1
F: 1s2 2s2 2p5
Rb: [Kr] 5s1
Es: [Rn] 7s2 5f11
Chapter 1d: Periodic table of elements
The table of Mendeleev is also called the periodic table of the elements. More than a simple list of the existing atoms. Mendeleev sorted the elements with regard to their oxidation/reduction by O/H
R20 R0 R302 RH4 RH3 RH2 RH R
Where R is the element. The atoms of same oxidation were sorted by weight to obtain the different lines. Some holes were present in the table but it was assumed that the missing elements were not yet discovered. Scientists have been able to fulfil the periodic table by the artificial synthesis of those elements. In the table showed above, the elements from 110 to 118 are theoretical.
It may not look like, but the determination of this table was a huge improvement for the chemists. The table contains a gigantic number of information for each atom, but also shows some periodic trends.
One case
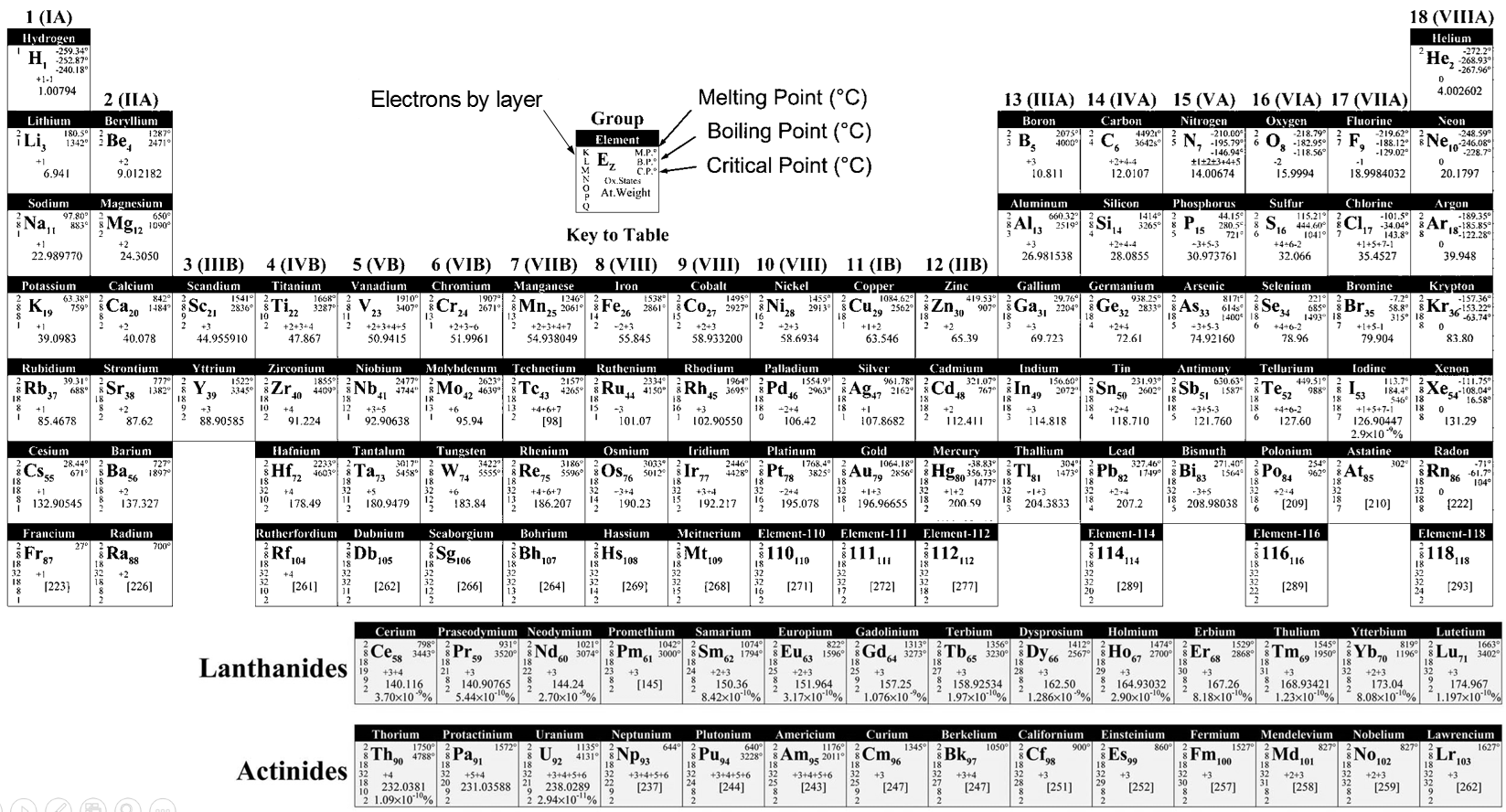
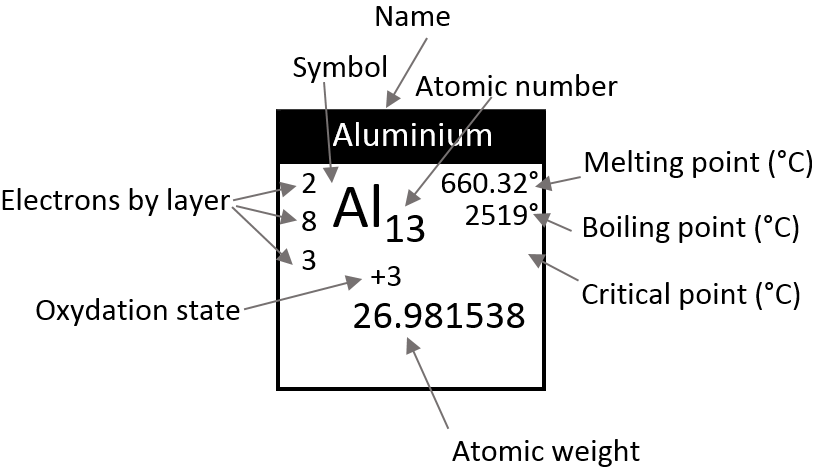
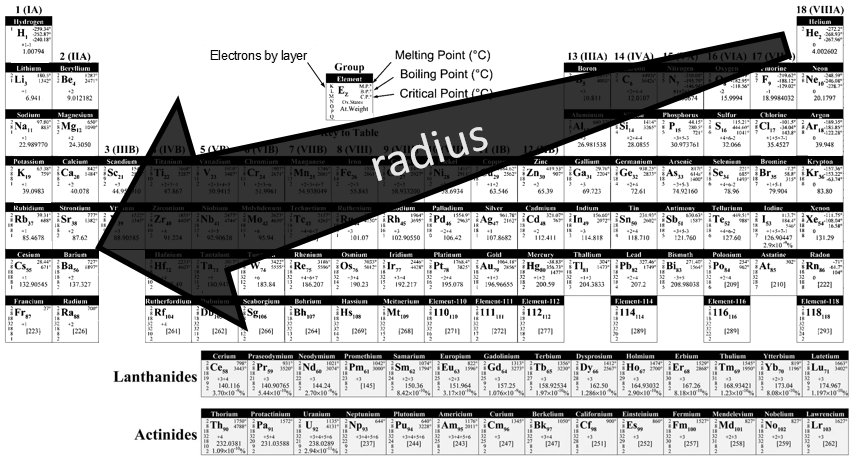
There is a large number of different models for the periodic tables. Some of them only show the symbol, name, atomic number (Z) and weight of each element but many other information can be displayed for each element. An example follows for the Aluminium.
Its symbol is Al, its atomic number is 13 and it has a weight of 26.981538 units of atomic mass (which is equivalent to the molar mass, in g/mol). The weight of an element is the average of the mass of its isotopes, taking in account their proportions. The weight is the property that we seek most of the times on a Mendeleev table. The number of electrons by layer can be determined from Z but is often indicated on the periodic table. Aluminium Z=13, meaning that the layer n=1 is complete with 2 electrons, the layer n=2 is complete with 8 electrons (2 in 2s2 and 6 in 2p6) and that 3 electrons are to be distributed in the n=3 layer. The 2 first electrons are in 3s2 and the last electron is in a 2p orbital. From that, we can determine that Al is on the third line of the table (n=3), in the third column (3 electrons are in the last layer).
Aluminium has a unique oxidation state (OS) of +3 (to be seen in a next section). Elements after the third column can have several OS depending on how they use their electrons. Finally, some temperature are indicated to let us know in which state, solid, liquid or gaseous, the element is found at a given temperature.
Lines
Each line corresponds to a value of n. Because a layer of electrons is added for each line, the radius of the elements increases when we are descending in the periodic table. The number of elements in a line is not identical from line to line, because the orbitals p and d are not present in the first lines. One can also see two particular lines at the bottom of the table, the lanthanides and the actinides, corresponding at the elements possessing an outer nf orbital.
Columns
The elements on a same column have the same number of electrons of valence. Each column is called a family and has a particular name. The three first columns and the 5 last are denoted Ia, IIa, IIIa,…,VIIIa and contain the main elements. In between are the transition metals, noted Ib, IIb,…
Ia (except H): alkali metals: they are all shiny (but tarnish in the contact of air), soft, highly reactive metals (in sctp, standart conditions of temperature and pressure) and readily lose their outermost electron to form a cation. They form strong bases when bound to OH– (NaOH,KOH).
IIa: alkaline earth metals: they are all shiny and reactive (in sctp). They readily lose their outermost electrons to form a cation of charge 2+.
IIIa: icosagens or triels: the column of Boron and Aluminium. They have 3 electrons in their outermost layer. Aluminium is one of the rare metals to have a low density.
IVa: crystallogens or tetrels: the group of the carbon and of the silicon. They have 4 valence electrons. Carbon is the essential component of living bodies (~23% of a human) but it is also a constituent of the earth through carbonates, and of the atmosphere through CO2. It is very resistant to heat. Silicon is a major constituent of the earth, second in abundance there. Si and C are in the same column but are surprisingly different. One of their common properties is that they can make long chains (C can make chains much longer than Si though). C can form pi liaisons while Si cannot because its radius is too large (no possible superimposition of the orbitals). CO2 is a gas while SiO2 is a solid (quartz) that is the base of the glass materials.
Va: pnictogens: the group of the nitrogen and of the phosphorus. 5 valence electrons, with two paired. They form stable covalent liaisons and can form double and triple liaisons. This ability to form persistent liaisons is the source of the toxicity of some elements of this group (arsenic, antimony). On the other hand, N2 is an inert gas which represents 78% of the air.
VIa: chalcogens: The group of the oxygen and of the sulphur. Oxygen has very different properties than the rest of this group: they are soft and do not conduct heat well. Oxygen makes up 21% of the atmosphere by weight, 46% of the earth’s crust by weight and 65% of the human body. Oxygen also occurs in many minerals, being found in all oxide minerals and hydroxide minerals, and in numerous other minerals. Ozone is spontaneously formed in the high atmosphere where it catches UV rays from the sun.
The emitted radical will react immediately with an adjacent molecule. The ozone is a better oxidant than O2 because a pi liaison is delocalised. As a result, ozone is often used to kill bacteria’s without waste.
VIIa: Halogens: All the halogens form acids when bound to a hydrogen and are generally toxic. They also from salts when bound to alkali’s.
VIIIa: Noble gas/Rare gas: those element are inert: they do not react with any other element. Helium is the most common element in the universe (~24% of its mass). Because of their lack of reactivity, there are used in lighting (also true for nitrogen)
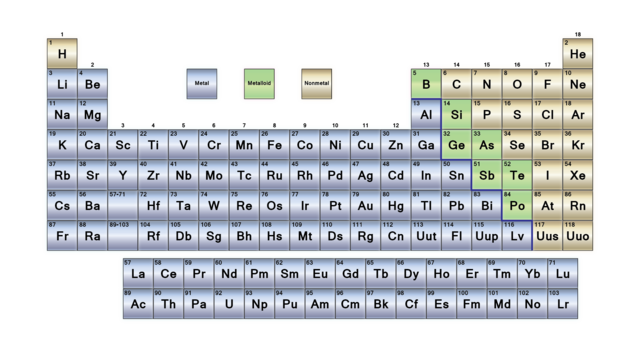
Metals, metalloids, nonmetals
The periodic table can be divided in three broad sections: metals, metalloids, nonmetals. These three categories are well regrouped in the table (except H, as always). Most of the elements are metals. The nonmetals are on the top right corner of the table (+H) and metalloids are only the elements on a diagonal from Boron to Polonium.
Metals
Metals have good thermal and electrical conductivity. As a broad category, they have common properties but exceptions exist for several elements for one or more properties.
They have in general a low ionisation energy, a low electronegativity and give or share their electrons when bonding. The bonding of two or more metals forms an alloy. Most of them can form oxides and are naturally found in this state.
In general, they are soft and malleable solids of high density but some are liquids in sctp (Hg for example). Most of them are silvery coloured.
Nonmetals
Most of nonmetals are low density gases in sctp. When bonding, they share or accept electrons and do not form basic oxides (but well acidic oxides as HClO, H2SO4, etc). In opposition to metals, they do not conduct electricity or heat well, and have a high ionisation energy and electronegativity. Usually, they are not naturally found in a combined state.
Metalloids
They are the minority of the elements. They look like metallic solids and can form oxides (acidic, basic or amphoteric). Most are semiconductors, and moderate thermal conductors, and have structures that are more open than those of most metals.
Periodic properties
Atomic radius
Several kinds of radius can be determined for a single element.
Crystalline radius: a crystal is a solid in which the atoms are spatially arranged. Monocrystals are obtained from the aggregation of atoms on one unique atom. They have the advantage of having less defaults in their structure than crystals arranged around several sources. Crystals are not necessarily a structure made of a single element. It is for example usual to make crystals from proteins to determine their spatial structure.
The method to obtain crystals is as follows: the element of the crystal is first dissolved in a solvent. The dissolution can be helped by an increase of the temperature. Once the dissolution is complete, the goal is to decrease very slowly the affinity of the element with the solvent. It can be done through the evaporation of the solvent (another solvent of lower affinity replaces the evaporated solvent) or if the solution was heated, through a slow decrease of the temperature. The process has to be slow to avoid the formation of several centres of aggregation.
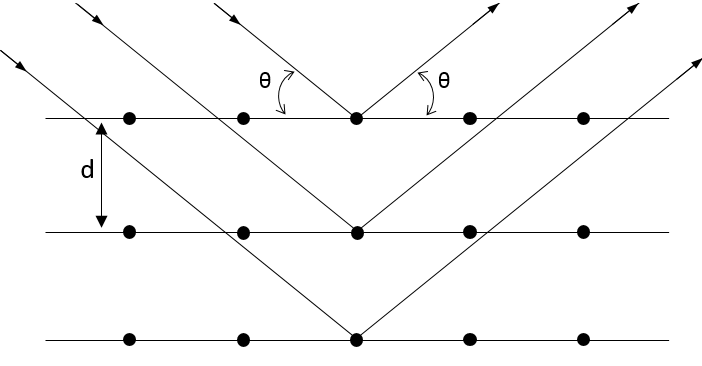
The structure of the crystals and the distance between atoms inside a crystal depends on its constitutive elements and can be determined by RX diffraction.
In this method, a RX beam hits the surface of a crystal with a given angle θ.
The interaction of this beam with the atoms of the first layers of the crystal. This interaction gives place to diffraction only if
Where d is the distance between layers in the crystal, θ the angle of incidence and λ the wavelength of the beam. This equation is the equation of Bragg. If this condition is not fulfilled, the interaction between the atoms and the beam are destructive (i.e. they are cancelling each other) and no diffraction occurs. The radius is the half of the distance between atoms in the crystal.
Calculated radius: we consider here that the radius for which the probability of presence of the electron is the largest is the radius of the atom.
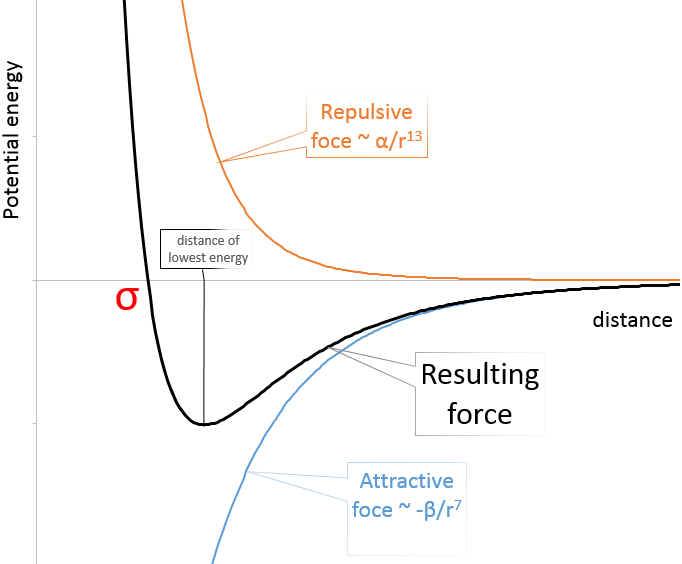
Van der Waals radius: The van der Waals radius is obtained by the addition of the repulsive force and the attractive force between two atoms. These two forces depend on the distance separating the atoms but not the same way. The attraction is proportional to the radius power -7 while the repulsion on the radius power -13. As a result, there is a favoured distance between the atoms when they bind. It is the attraction pit. Reducing this distance increases drastically the potential energy. σ is the distance of smallest approach and is the crossing between the curve and Epot=0. Increasing the distance also increases the potential energy towards 0.
The radius of the atom can be determined from σ.
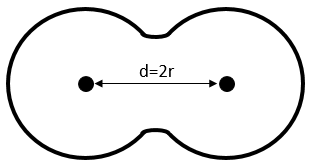
Covalent radius: for diatomic molecules, the radius of the atom is considered as the half of the liaison’s length.
Empirical radius: it is obtained from the volume of the atomic gas. In a given volume of gas, there is a given number of atoms. Considering spherical atoms, the volume of one atom is V=4/3π r3. Therefore the radius is determined.
Those different radius are not equals and in some case they do not exist. For example, there is no covalent radius for He.
However, each of them follows the same logical repartition in the periodic table:
As we have seen in the previous section, a layer of electrons is added at each new line of the periodic table. It is thus logical that the radius of the elements increases in a single column. Moving across a line, the number of protons in the nucleus increases and the outer electrons are thus more and more attracted by the nucleus. From left to right, the radius decreases. As a result, Li and Mg have a similar radius, as do Na and Ca.
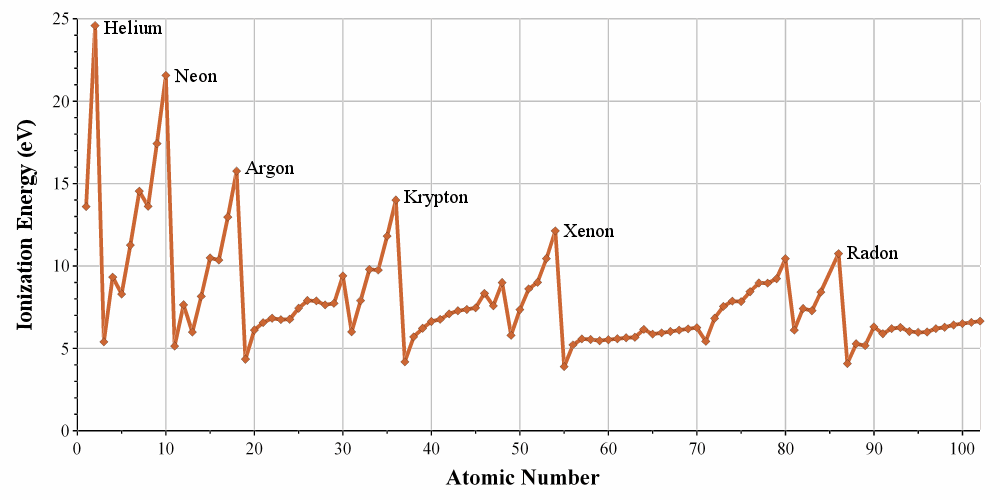
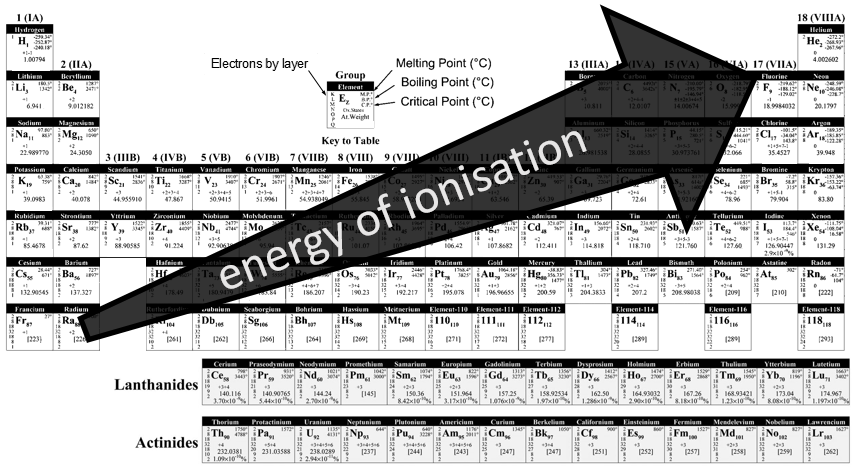
Ionisation energy
The ionisation energy (IE) is the energy required to remove one electron from an atom of a gas.
This energy is positive (atoms in gas don’t lose their electrons spontaneously) and depends on the energy of the electron: an electron close to the nucleus is hard to remove. It is also way more difficult to remove a second electron from an atom which had already lose one. For example, the aluminium has the following ionisation energies:
The first electron is relatively easy to remove: it is the single electron on the orbital 3p of the aluminium. The next electron is way more difficult to remove: it is an electron on a complete orbital. The third energy of ionisation is small for a third ionisation: we obtain the electronic structure of the noble gas Neon: the octet is complete and this structure is stabilized. This stabilisation is visible in the next energy of ionisation: a gigantic energy is required to remove one additional electron.
The energies of ionisation are periodic on the Mendeleev table. It requires a massive energy to remove an electron from a noble gas but it is easier to go towards its electronic structure. In one period/line, one can see that the trend of the IE is not linear. It is more difficult than average to remove an electron from a complete orbital
It is easier to remove one paired electron (less repulsion)
It is easier to empty one orbital: the last electron is shielded by the electrons of inner orbitals.
For the same last reason, the IE decreases when moving downwards in the periodic table: the shielding effect is bigger and bigger with the number of layers of electrons.
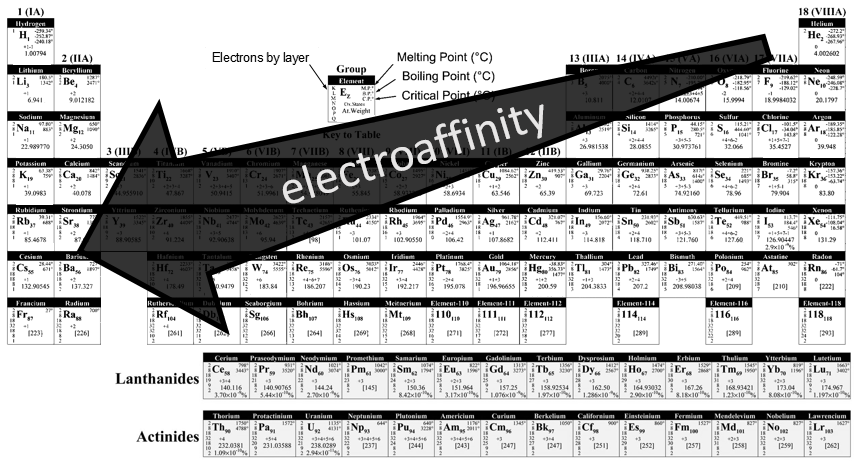
Electroaffinity
The electroaffinity is just the opposite of the ionisation: it is the energy required by a gaseous atom to accept an additional electron and follow the opposite evolution than the IE.
Note that noble gases don’t have any electroaffinity because they are inert.
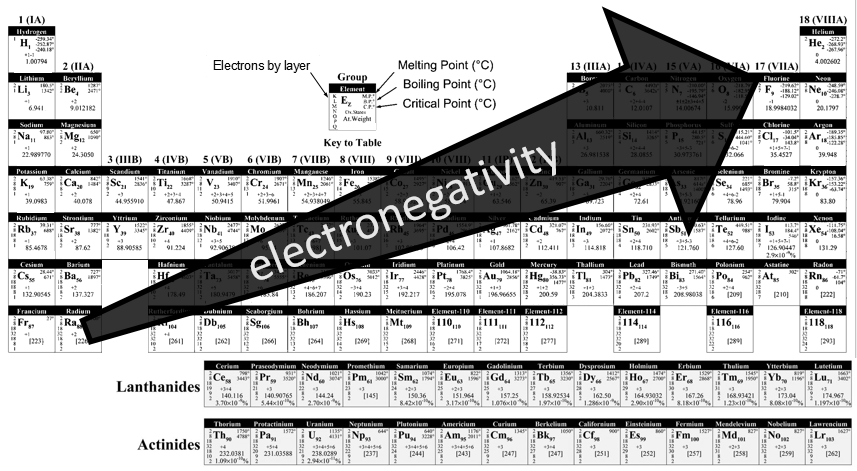
Electronegativity
The electronegativity is an important notion in chemistry: it is the ability of an atom to attract the electrons of a liaison it shares. The symbol for the electronegativity is χ.
Pauling determined that, by convention the fluor, being the atom of largest electronegativity, has χ =4. The other elements have an electronegativity given by
Where DXY is the energy of dissociation between X and Y, i.e. the required energy to break a liaison between X and Y.
The fluor being in the top right corner of the table, it is not difficult to understand the trend for the electronegativity.
Exercises
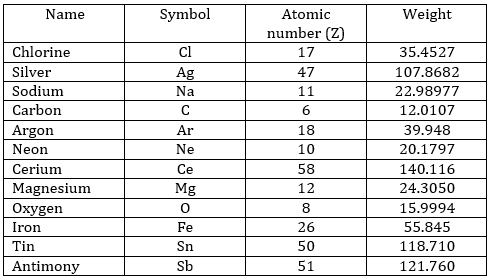
- What is the symbol, atomic number and weight of the following species?
Chlorine, silver, sodium, carbon, argon, neon, cerium, magnesium, oxygen, iron, tin, antimony
- Name the following species:
O2, NaCl, 10n, HNO3, SnBr4, 21H, P2O5, H2S, HClO2, CO2, HClO3, HNO2, HClO4.
- What is the molar weight of the above cited species?
- What is the formula of
Carbon monoxide
phosphorous acid
sodium bromide
dinitrogen trioxide
hydrogen peroxide
- How much perchlorate of calcium do we have to weight if we want 50 moles of it?
- How many molecules of AgI is there is 20g?
- Which element has a higher electronegativity?
- F or I
- Na or Cl
- Mg or Ar
- Which element has a higher energy of ionisation?
- I or Br
- C or F
- P or Na
- Which element has a larger radius?
- Al or S
- Li or O
- Sn or Rb
- Chlorine has two stable isotopes: 35Cl and 37 Their masses are 34.96885 and 36.96590. What are is the proportion of both of the isotopes knowing that the atomic mass of the chlorine is 35.4527?
- The mass of 0.1726mol of an acid HXO4 is 25g. Determine the element behind X.
- How many valence electron in halogens? In earth-alkalines?
- What are the names of those reactions?
Answers
- What is the symbol, atomic number and weight of the following species?
Chlorine, silver, sodium, carbon, argon, neon, cerium, magnesium, oxygen, iron, tin, antimony
- Name the following species:
O2: oxygen
NaCl: Sodium chloride
10n: neutron
HNO3: nitric acid
SnBr4: tin (IV) bromide
21H: deuterium
P2O5: phosphorus pentoxide
H2S: hydrogen sulphide
HClO2: chlorous acid
CO2: carbon dioxide
HClO3: chloric acid
HNO2,: nitrous acid
HClO4: perchloric acid
- What is the molar weight of the above cited species?
O2: 32g/mol
NaCl: 58.44g/mol
10n: 1g/mol
HNO3: 63.01g/mol
SnBr4: 438.33g/mol
21H: 2.01g/mol
P2O5: 141.95 g/mol
H2S: 34.08 g/mol
HClO2: 68.46 g/mol
CO2: 44.01 g/mol
HClO3: 84.46 g/mol
HNO2,: 17.18 g/mol
HClO4: 100.46 g/mol
- What is the formula of
Carbon monoxide: CO
phosphorous acid: H3PO3
sodium bromide: NaBr
dinitrogen trioxide: N2O3
hydrogen peroxide: H2O2
- How much perchlorate of calcium do we weight if we want 50 moles of it?Formula of the perchlorate of calcium: Ca(ClO4)2Its molar mass is: M=40.078g/mol+ 2x(35.4527g/mol + 4×15.9994g/mol) =238.9786g/molThus, 50mol of it weight 11.948kg.
- How many molecules of AgI is there is 20g?1 mol of AgI weights 234.77267g. There are thus 0.085mol of AgI in 20g. The question is how many molecules are in 20g of AgI. In one mole, there are NA (the Avogadro number=6.022 1023) molecules. That makes 5.13 1022 molecules.
- Which element has a higher electronegativity?
- F or I
- Na or Cl
- Mg or Ar (Ar is a noble gas, so it does not accept any additional electron)
- Which element has a higher energy of ionisation?
- I or Br
- C or F
- P or Na
- Which element has a larger radius?
- Al or N
- Li or O
- Sn or Rb
- Chlorine has two stable isotopes: 35Cl and 37 Their masses are 34.96885 and 36.96590. What are is the proportion of both of the isotopes knowing that the atomic mass of the chlorine is 35.4527?
To solve this, we have to consider 2 things:
- The atomic mass of an element is the average of the masses of its stable isotopes. So 35.4527=x 34.96885 + y 36.96590 where x and y are the proportions of each isotope.
- The sum of the proportions of the isotopes is 100%: 1 (100%)= x + y.
We have thus two equations with 2 unknowns. That can easily be solved:
The proportions are thus 24.23% of 37Cl and 75.77% of 35Cl.
11.We determine first the molar weight of the acid:
The mass of X is the molar weight of the acid minus the known atoms:
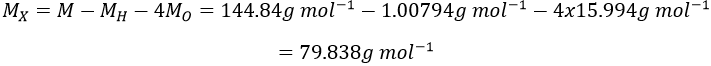
X is thus the bromine Br.
12. 7 in halogens, 2 in earth-alkalines
13.
Chapter 1f: Redox reactions
Oxido-reductions, or redox, are reactions involving a transfer of charge between molecules. During such reactions, some chemical energy is transformed into electrical energy.
An oxidation reaction is a reaction during which a substrate (molecule, atom or ion) loses electrons.
A reduction reaction is a reaction during which a substrate gains electrons.
An oxidant is a substrate with the ability to oxidize other substances. During this process, the oxidant is thus reduced. They are also called oxidizer or oxidizing agent.
A reductant is a substrate with the ability to reduce other substances. During this process, the reductant is thus oxidized. They are also called reducer or reducing agent.
The state of oxidation
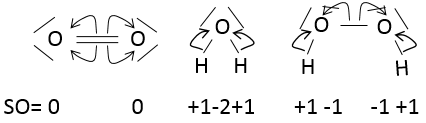
The state of oxidation (SO) is an integer the value of which is the charge of an atom if we break all its liaisons. In O2, each atom takes its electrons back (it is a homolytic cleavage or homolysis). The global charge of O2 is neutral. Thus the SO of each oxygen is 0. However, in H2O, the oxygen takes the electrons from the hydrogen’s when we break the liaisons because the oxygen is more electronegative than the hydrogen (it is a heterolytic cleavage or heterolysis). The SO of oxygen in H2O is -2 and the SO of the hydrogen’s is +1.
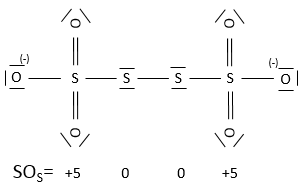
In general, the SO of the oxygen is -2 and we can find the SO of the other atoms of the molecule without the full representation of the molecule. For example, we can determine the state of oxidation of the manganese in MnO4–: the global charge is -1 and each oxygen has a SO of -2. The SO of Mn is thus +7 so that the global charge equals the sum of the states of oxidation -1=+7-(4x-2). In heavy water, H2O2, the SO of the oxygen’s is -1.
An atom can thus have several possible SO. If several SO are present for one atom in a single molecule, we take the average between them. For example, S has a SO of +2.5 in S4O62-. Sulphur can have a SO from 0 (solid sulphur) to +6 (H2SO4).
Redox reactions
So, in a redox reaction, an oxidant oxidizes a reductant while the reductant reduces the oxidant. In presence of two compounds, it is however not always obvious to determine the direction of the reaction
This reaction involves two half reactions:
The reaction will go in the direction that has a negative enthalpy. In the present case, the reaction goes from left to right and it can be explained because Cu is more electronegative than Zn. It is thus harder to take its electron from Cu than from Zn.
It is possible to determine the strength of the oxidants and reductants from their ability to attract electrons in a battery, i.e. their standard potential ε0 (in volts). However, an absolute value of the standard potential is not measured. We can only know the value of ε0 with regard to another couple. We use the couple H+/H2 as a reference, with its standard potential set to ε0=0.000V in sctp by convention. The name of a couple is put in the direction of the reduction: oxidant/reductant. For example: Cu2+/Cu, Zn2+/Zn.
To establish a redox reaction correctly, a method exists:
First, we write the supposed equation without stoechiometry, protons, water or OH–. Just the oxidants and reductants. We determine their state of oxidation
Second, we determine the individual standard potentials of each couple. The values of ε0 can be found for a large range of compounds on the back of Mendeleev tables. It is given for the reduction reactions (for the oxidation, take the negative value). For the iron, the reaction is
For the manganese, 5 electrons are added to obtain Mn2+.
Be careful to consider how many atoms are reduced/oxidized. In the couple Cr2O72-/Cr3+, Cr has a SO of +6→+3 but 6 electrons have to be added in the reaction because two Cr are reduced.
Coming back to the problem involving manganese, the reaction is not balanced yet. Oxygen’s are also involved in the process. We balance the reaction with water molecules, protons or OH– depending on the acidity of the solution. To determine how many species are required, we count the charges at each side of the arrow:
There are 6- at the left because MnO4- is negatively charged. The difference of 8 charges is balanced by the addition of 8 protons at the left of the arrow and we balance the equation:
The standard potential of this reaction is known. Now, we put together the two half reactions. Don’t forget to consider that one half reaction introduces 5 electrons and the other one introduces 1 electrons. The equation of Fe3+/Fe2+ is thus multiplied by 5.
This final reaction is correctly balanced. Note that even if the half reaction Fe3+/Fe2+ is multiplied by 5, it is not multiplied in the determination of the standard potential. As Δε0>0, it means that the reactions goes from left to right. This reaction is spontaneous if the production of enthalpy ΔG0<0. The enthalpy of reaction is a measure of the work required to do the reaction. If this value is negative, the reaction is spontaneous and liberates energy, generally in the form of heat. The reaction is said to be exothermic. If this value is positive, it is necessary to give some energy to do the reaction. The reaction is endothermic as it absorbs heat from its surrounding.
The relation between the enthalpy of a reaction and its potential is
This relations comes from the fact that a potential V is the variation of work J to modify the charge Q
Batteries
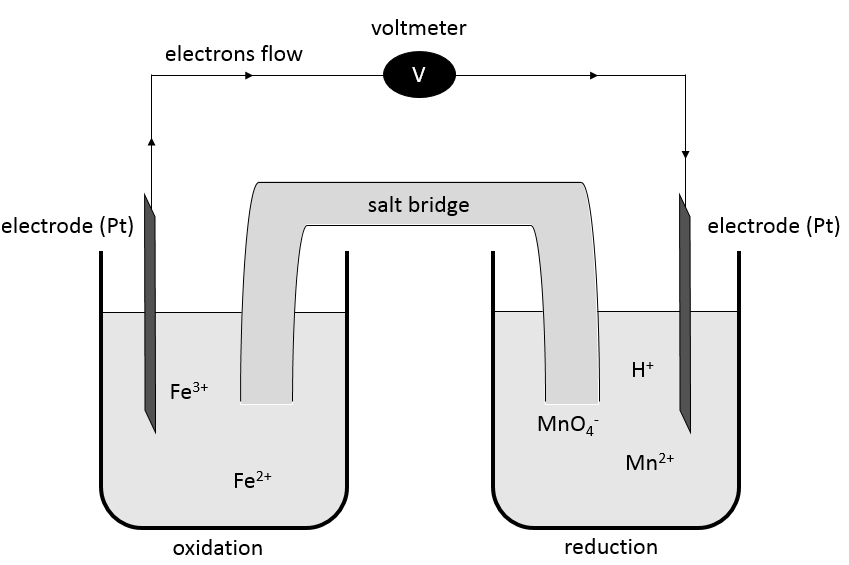
In batteries, the elements of a redox reactions are separated. The two solutions are connected by a salt bridge and two electrodes connected to a voltmeter.
A salt bridge is a device used to connect two half batteries, that is full of ionic species conducting electricity (electrolytes) but not interfering with the compounds of the battery. Without the salt bridge, one half cell would accumulate negative charge and the other half cell would accumulate positive charge as the reaction proceeds. The cations and anions of the half bridge are chosen so that they have a similar high conductivity. KCl, KNO3, NH4Cl are some examples of electrolytes composing a salt bridge.
A battery is written by convention as follows:
The electrodes are put at the extremities and the compounds of the two half batteries are separated by a double line symbolizing the salt bridge. The oxidation is put in first and the reduction in second.
The oxidation of Fe2+ is done at the electrode of platinum that catches the freed electron. This electron goes through the voltmeter to the other half battery where it is used in the reduction. The salt bridge closes the electric circuit.
The potential of a battery, also called electromotive force, is given by the Nermst equation and depends on the concentrations of the different species:
We can also obtain the potential from the difference between the two cells of the battery:
Be careful that the concentrations of Fe2+ and Fe3+ were inverted in the last equation because we consider the products and reactants of the half batteries in this case.
In a battery of concentration, the electromotive force is only given by the concentrations of the species:
The two sides of the battery have the same ε0 and the equation for the electromotive force is thus limited to
Here, we cannot use KCl as electrolyte because Cl– would react with Ag+ to form a precipitate of AgCl.
Electrodes of reference
An electrode of reference is an electrode the potential of which is known and does not varies during an experiment. The standard hydrogen electrode (SHE) is a first electrode of reference but is not often used because it is not entirely reproducible.
Dihydrogen gas is introduced in an acid solution of 1M with a pressure of 1atm.
The silver chloride electrode is used as electrode of reference
The potential of the electrode depends on the concentration of the ionic form of Ag.
However, this concentration also depends on the solubility of AgCl in water
The constant of dissolution of AgCl is KS=[Ag+][Cl–]. By saturating the solution with KCl (>3.6M), the concentration of chloride is constant, hence the fixed concentration of Ag+.
The potential written above is not totally correct because at large concentrations, the concentration is no more equal to the activity of an ion.
The saturated calomel electrode uses the same principle:
Here the mercury cations precipitate with chloride which is saturated the same way as for the silver chloride electrode
The reverse of a battery is the electrolyse: a current is applied in a cell to induce a reaction with a negative electromotive force. It is a way to depose metals from a solution.
The quantity of deposed metal depends on the applied current:
All the first column of the Mendeleev table are obtained by electrolyse. In the nature, they exist in their oxidised form because the world is oxidant: H2O and O2 are everywhere. The production of Na can be done from its salt by electrolyse:
This reaction is performed at high temperature (>600°C) and in total absence of water.
Disproportionation
In some cases, a single species plays simultaneously the role of oxidant and reductant. A reaction involving such a process is called disproportionation. The salt of copper dissociates in water in Cu+ and Cl-. However solid copper is obtained during the process. It is a consequence of the disproportionation of copper:
As the second reaction has a larger potential, the global reactions forms solid copper:
The Cu+ dissociated from CuCl forms spontaneously Cu2+ and Cu(s).
Monoxide of carbon is the result of disproportionation between CO2 and C. It is a process responsible of many incidents, often lethal, in bathrooms with an insufficient ventilation. Traces of carbon, obtained from burned organic compounds, reacts with the carbon dioxide emitted by boilers or heaters. The problem is that CO takes the place of O2 on our blood cells and is much strongly bound to them than O2 (by a factor 200). Once CO is bound to a blood cell, O2 can difficulty bind, Because of that, only a small proportion of CO can be catastrophic. To treat people affected by CO, they are placed in a room overpressured with O2 to force the equilibrium and remove the carbon monoxide.
The standard potential of a reaction can be found from its intermediate reactions.
In total, 3 electrons are required to obtain the iron on its solid state. 1 electron is required for the first step and 2 for the second step. The (approximate) standard potential is found by a combination of the standard potential of each step, taking in account the required electrons for each step:
In total, the process has a negative standard potential. The reverse reaction is thus spontaneous in presence of an oxidant. It is the production of stain (hydrated Fe3+) from iron. On a car for example, the iron is protected by a thin layer of painting/coating, not allowing water to the contact of the iron. If there is a default on the coating, the iron is oxidised but the stain will not always appears at this location: the electrons freed by the oxidation can move through the metal.
To avoid this, surfaces are connected by an electric cable to a piece of zinc. The zinc will oxidise instead of the iron because its standard potential is smaller.
Stain is a porous material and the oxygen can pass through it to proceed further. ZnO is not porous so a monolayer of Zn can protect iron pieces from stain. It is the principle of stainless iron, but applied with Cr2O3.
Chapter 1: history of chemistry and chemical reactions
It is often useful to take a look on the history of something to understand it. That is how we will begin our lessons about chemistry. As far as we can go, chemistry started with the discovery of fire, which is basically the combustion of a reactant to obtain heat from it. Later, different metals were discovered, giving the names of the iron, copper and bronze eras.
However, we can’t talk about a scientific method at this moment yet. It is more about evolution. Evolution is a process to adapt best to our environment, most of the time through a trials and errors process. Processes which lead to a better adaptation were repeated while the others were not. Fire for example gave a huge improvement to the life of men for now obvious reasons but yet the process was not deeply understood.
Rationalisation is first seen with the Egyptians (fabrication of glass, beer and coloring), China (porcelain) and then with the Greeks. It is Leucippe and then Democrite who describe the matter as composed of small unbreakable particles, the atomos. Greeks also claimed that the world is composed of 4 main elements: earth, water, air and fire. We could now compare those to the three main phases: solid, liquid, gaz and the energy
The scientific method was developed during the XVI century. The method consists in 3 steps:
- Observation of a phenomenon: gives quantitative and qualitative information
- Hypothesis: tries to give possible explanations to the observed phenomenon
- Experiments: gathers new information on the phenomenon, confirm or not the theories developed in the previous step.
Before that, men described what they saw. From that point, men try to explain what they see through theories.
Stoichiometry and determination of the atomic masses
One of the fathers of the modern chemistry is Lavoisier. The statement he is known for is “Nothing is lost, nothing is created, everything is transformed” which meant that the total mass of the product of a reaction equals the total mass of the reactants. This statement is indeed true except for nuclear reactions during which a part of the mass is converted into energy.
Joseph Proust stated that a chemical compound always contains exactly the same proportion of elements by mass. For example, in pure water, the mass of hydrogen is always 1/9 of the mass of the sample while the oxygen makes up the 8/9 of the mass.
To complete this law, Dalton observed that during a reaction, the masses of the compounds which react together are always in a relation of simple integers. For example oxygen (O) and carbon (C) can react together in several ways
1g of C + 1.33g of O → 2.33g of CO
1g of C + 2.66g of O → 3.66g of CO2
to form carbon monoxide or carbon dioxide. The relationship between the mass of oxygen is 1 to 2. This is the basis of the stoichiometry. Bertholet protested against that law because one of his experiments gave opposite results. This experiment involved a solid of CuO wherein the ratio between Cu and O is neither constant nor a simple integer. The reason is that solids may have imperfections. Basically, these imperfections can be empty spaces or atoms replaced by others. This is why Bertholet obtained a formula of Cu1-xO instead of CuO.
Dalton established an atomic theory:
- All matter is made of atoms. Atoms are indivisible and indestructible.
- All atoms of a given element are identical in mass and properties. Atoms of different elements are different.
- Compounds are formed by a combination of two or more atoms. There is no formation of new atom (except nuclear reactions).
- A chemical reaction is a rearrangement of atoms.
The mass of each element has been determined. First works were performed by Cannizzaro, basing its experiment on a principle enounced by Avogadro: In normal conditions of temperature and pressure, identical volumes of gas have the same number of particles. Knowing the proportion of carbon there is in different gases, Cannizzaro determined its mass:
| Compound | Mass (g) | % of carbon | Mass of carbon (g) |
| Methane | 16 | 75 | 12 |
| Ethane | 30 | 80 | 24 |
| Propane | 40 | 82 | 36 |
The mass of C was determined this way. C has a mass of 12 atomic mass units (u). Consecutively, the mass of oxygen (16) has been determined from carbon dioxide (CO2). And so on. Initially, some errors occurred, typically because of elements with an even mass. For example, it was known that 2g of H react with 16g of O to form 18g of water. Considering the simplest relation, H has a mass of 1u (which is correct) but O would have a mass of 8u.
Moles and the Avogadro’s Number
The mole is one of the seven units of the International System of Units (SI Units): kilogram for mass, meter for length, second for time, Kelvin for temperature, ampere for electric current, candela for luminous intensity and mole for the amount of substance. The symbol for mole is mol.
Coming back to Avogadro, one of the most important numbers in chemistry, but almost never used is the Avogadro’s Number NA. As atoms are unbreakable, there are obviously several atoms in 12g of C. A mole expresses the number of atoms of carbon in 12g of carbon.
MC=NA.mC
This relation is true for any element i. Mi is the molar mass of i, i.e. the mass of one mole of the element i. Its units is g/mol (or g mol-1). mi is the mass of one atom of the element i. In the case of the carbon, MC=12g mol-1. mC being a mass, NA unit is mol-1. The value of NA was initially determined by Johann Josef Loschmidt who calculated the number of particles in a given volume of gas. The accuracy of the measure was perfectible and there are now experiments which give more accurate results than this method.
NA= 6.02214129(27)×1023 mol−1
Ourself and our environment is thus filled by an amazingly large number of atoms that interact together to form matter, air, liquids and most importantly life. The idea that molecules from the living could be crafted was not accepted before the XIX century. Friedrich Wöhler, a german chemist, can be considered as a pioneer of the organic chemistry. At this time, the hypothesis of vitalism was popular: any compound, to be living, needs a vital force given by God. Humans should not be able to synthesize, without this vital force, any organic compound. Wöhler proved that this theory was wrong by producing urea, accidentally, from inorganic substances. Even if urea is a waste of our body (when we pee), it is an organic compound and it should have been impossible to Wöhler to synthesize it without the intervention of the vital force from a living species. Friedrich Wöhler wanted to produce ammonium cyanate from potassium cyanate (KNCO) and ammonium chloride. However, the target product is unstable and acts only as an intermediary product, decomposing itself into urea.
Stoichiometry
The stoichiometry is the relation between the quantities of reactants and products during a chemical reaction.
A chemical reaction is written by an equation, placing the reactants on the left of an arrow and the products on the right of it. There can be several reactants that react together to form one single product. Each species is separated by a +.
In this reaction, hydrogen and oxygen are mixed to produce water (H2O). Hydrogen and oxygen are separated by a + at the left of the arrow because they are the reactants and the water is at the right of the arrow because it is the product of the reaction. Several products can be formed from one or more different reactants.
In this case, two products are generated by the chemical reaction: water and carbon dioxide. They are also separated by a + and are still at the right of the equation.
Now, the equations are not complete. We have to respect the law of conservation of mass (of Lavoisier): nothing is lost, nothing is created, everything is transformed. The quantities of an atom at the left and at the right of a chemical equation have to be identical. In the first equation, we wrote that one mole of H2 reacts with one mole of O2 to form one mole of H2O. The number of H is equal before and after the reaction (there are 2 of them in H2 and 2 in H2O) but one atom of oxygen would be lost. To obtain the correct equation, we put coefficients, called stoichiometric coefficients, before the species:
It is thus 2 moles of H2 that react with one mole oxygen to produce two moles of water. Here, the quantities of each atom is identical at each side of the arrow. This notation is also correct, as long as the numbers of atom are integers:
The second equation that we wrote was also incorrect:
The number of carbon C is correct, but the quantities of H and of O changed during the reaction. As there are 4 hydrogen at the left, we will put a coefficient 2 in front of the water to have 4 H at the right of the equation. Now, we have 4 oxygen’s in the products and only 2 in the reactants. To correct the equation, a coefficient 2 is put before the O2. The number of C is still correct and the equation is
There can be some variations to this notation. If a specific solvent is required for a reaction to happen, we indicate it above or under the arrow.
This reaction is the dissolution of salt (NaCl, also called table salt, the salt that we add on our food) into water. The elements of the salt are separated into the corresponding ions, i.e. charged species. The positively charged ions are called cations and the negatively charged species are called anions. If we need to heat the solution for the reaction to happen, we will also indicate it near the arrow by a Δ or a ΔT.
A reaction that requires heat to be made is an endothermic reaction. If the reaction generates heat, this reaction is said to be exothermic. Note that in the previous reaction, we indicated the states of the compounds between brackets. The g means that the species are gaseous. A s means that it is a solid, l stands for a liquid and aq stands for an aqueous solution. The heat generated by an exothermic reaction is written just as a product by Q or its exact value in kJ/mol if it is known. Some reactions produce light, also indicated as a product by hν, i.e. a photon of frequency ν.
The last point to talk about is that all the reactions are not complete. A complete reactions means that, if the reactants are put in stoichiometric proportions, all the reactants will be consumed during the reaction to form the products. If one reactant has more than the stoichiometric proportion, it is in excess and there will still be an amount of this reactant after the reaction, corresponding at the excess. During incomplete reactions, called reactions of equilibrium, all the reactants are not consumed even if they are put in stoichiometric proportions. There is an equilibrium between the quantities of reactants and of products of this reaction. Incomplete does not mean that the products are not fully made, but only that a part of them are generated. For example, the acetic acid is a low acid that does not completely dissolve in water.
As a result, we find the three species in solution: CH3COOH, CH3COO– and H+. Some of the reactants formed the products and some did not react. Note that the arrow in the chemical equation is different from the one of complete reactions. It is now two half arrows meaning that the reaction can go in both sides. For equilibrium reactions, we define a constant of equilibrium K such as
The [] means that we consider the concentrations of the species between the [] power their stoichiometric coefficient.
Exercises
1. Equilibrate those equations
2. If we put together 2g of Br2 and 1g of H2, how many moles of HBr can be produced? What is the mass of the excess of reactant?
3. Write the general equation for the combustion of the organic compounds CxHy and CxHyOz
Answers
1.
2. The reaction consumes 1 mole of each reactant to form 2 moles of HBr
As Br has the biggest molar mass, H2 will be in excess.
As a result, only 0.025mol of H2 is consumed and 0.05mol of HBr is produced by the reaction. The excess of H2 is 1.959molà1.975g of excess.
3. A combustion reaction is the reaction between one reactant and oxygen. From organic molecules, it generates CO2 and water.
Chapter 2a: acid-base reactions
In this module we will review one of the main types of reaction of chemistry. Reactions can indeed be classified in 3 major categories:
- Acid-base reactions
- Redox (reduction and oxidation) reactions
- Solubility reactions (dissolution and precipitation)
The two last reaction types are seen in other sections of our lessons. We will here focus on acid-base reactions. The first step will be to introduce the definitions of acid and basic compounds and the notion of acidity. We will see next the strength of different acids and bases and explain how to follow experimentally the neutralisation of an acid by a base.
Definitions
A proton is a Hydrogen (H) atom that lost its electron (e–). Consequently, a proton consists only in one nucleus, which is positively charged. The proton is an ion: a charged molecule. We have here to consider that the nucleus of an atom is only a very small fraction of the volume of an atom (radius of ![]() ). Because of its small size, a proton can diffuse in everything and move through any material until its neutralization.
). Because of its small size, a proton can diffuse in everything and move through any material until its neutralization.
Several definitions were given to an acid and a base. Arrhenius proposed
- An acid is a donator of protons
- A base is a donator of OH–
This definition works well for several compounds, for example:
However, some basic compounds do not possess any OH group in them and can still neutralize acids. For example NH3 can react with H+ but cannot free any OH-. A tentative of explanation was to introduce NH4OH
but this compound does simply not exist.
Brønsted and Lowry proposed another theory:
- An acid is a donator of protons
- A base is an captor of protons
When a base reacts with an acid, they form respectively their conjugate acid and conjugate base
Considering any acid HA, the equation can be written:
HA loses a proton to form its conjugate base A–. The base B receives the proton to form its conjugate acid HB+.
An interesting point of this theory is that the acidity of a compound depends on the reaction in which it intervenes. It allows to some compounds to be both an acid and a base. For example, H2O can donate or receive protons.
Such compound is called amphoteric. In water, there is thus both acid and base in water. However, when we drink or put a hand into water, we don’t feel those substances (note that the water that we usually use in our everyday tasks contains ions, modifying its taste and slightly its acidity). As explained earlier, an acid attacks deeply into materials. Bases on the other hand affect surfaces by removing their protons. So why is nothing happening? The reason why is because the three substance (H2O, H3O+ and OH–) are in equilibrium. The reaction just above goes in both directions, as it is shown by the double arrow. However, the reaction doesn’t go in both directions at the same speed. The equilibrium constant for the reaction going from left to right is Kw=10-14mol2l-2=[H3O+][OH–]. For the other direction, the constant is K=1/Kw=1014mol-2l2. That means that the equilibrium is highly oriented towards the left. It is not frequent that a molecule of H2O autoprotolyses and when it occurs, the inverse reaction is very fast.
From Kw, we can determine the concentration of protons (or H3O+) in water.
Because H3O+ and OH– are produced at the same rate, their concentration is equal: [H3O+]=[OH–]. Then
In pure water, the concentration of protons is thus 10-7M (M=mol/l) at any moment. If an acid is put into water, the amount of protons in solution will increase. Inversely, if a base is put in water, the amount of protons decreases. The acidity of a solution is thus measured by the concentration of protons in the solution. For more comfort, the scale, called potential Hydrogen or pH, is minus the logarithm of the concentration of protons
and goes from 0 to 14 in aqueous solutions. At pH=0, the concentration of protons in solution is 1M. At pH=14, barely all the protons are removed from the solution by the base. The pH is not infinite because there is always a few protons remaining in the solution, due to the equilibrium. pH=7 is the neutral pH and is the pH of pure water. Most of the living species are adapted to this neutral pH. Some others have adapted to basic or acidic conditions to avoid predation or concurrence for resources.
We can also talk about pOH for bases with pOH=-log [OH–]. pOH is however generally not used. For basic aqueous solution, it is easier to refer at pH=14-pOH=14+log[OH–].
Lewis acids and bases
The same year, Gilbert Newton Lewis proposed an alternative, and broader, definition for acids and bases: A Lewis base is defined as a compound that can donate an electron pair to a Lewis acid, a compound that can accept an electron pair. Considering the same notation as above,
The two dots in this notation represents the pair of electron that the Lewis base B and the conjugate base A– are carrying. The proton is a Lewis acid, accepting pairs of electrons. With such a definition, the acids are no more limited to substances carrying hydrogen atoms. For example BF3 is a Lewis acid as the bore can accept a pair of electron.
Dissociation of H and OH
It is to be noted that in some occasions, H is not dissociated as a proton. When the liaison between two atoms is broken, the pair of electrons remains with atom of greater electronegativity (χ–).
Examples:
H-Cl: χ–Cl=3.16 χ–H=2.2
In this case, and as expected, the pair of electrons remains on the chloride atom because its electronegativity is larger than the one of the Hydrogen.
Na-H: χ–Na=0.93 χ–H=2.2
The Sodium hydride is one of the few exceptions where the Hydrogen atom takes the pair of electrons. Indeed, its electronegativity is very low in comparison with H. This molecule splits in Na+ and H–.
If we look now to the liaison OH:
χ–O=3.44 χ–H=2.2
This group, typical in the basic compounds, can break to free a proton. A molecule carrying a OH group may then be acidic or basic depending on the atom connected to the oxygen.
In NaOH for example, the electronegativity of Na (χ–Na=0.93) is smaller than the one of the hydrogen (χ–H=2.2), by far. As a result, it is the bond between Na and O that breaks. As the O is already negatively charged, the O-H bond won’t split to give O2- and H+.
On the contrary, in HClO (Cl-O-H), the electronegativity difference between Cl-O is larger than the one between O-H. As a result, the hypochlorous acid splits in ClO– and H+.
To resume, the acidity of a substance depends on the reaction in which it takes part, and the presence of a H or a OH group in the substance does not mean that it is an acid or a base, and vice versa the fact that a substance is acidic or basic does not mean that this substance carries a H or OH group.
Measure of pH
Different methods exist to measure or to give an idea of the pH of a solution.
pH indicator
When a few droplets of pH indicator are added to a solution, the pH indicator gives the solution a colour depending on the acidity of the solution. Into a given area of pH the solution will be of a certain colour while the colour is different into another area of pH. Those area are not specifically 0-7 and 7-14 and depend on the pH indicator used. The change of colour is due to interactions between protons and the molecules of the pH indicator.
For example, bromocresol green is yellow in its acidic form and blue in its basic form. There is a transition area of pH for the bromocresol green between the pH from 3,8 to 5,4 where its colour is green, the colour of “its neutral form” (in fact it is a mix of the acidic and the basic forms). The structure of bromocresol green is shown is the Figure 1. The colour of the solution does not vary sensibly in the same area of pH but only at the limits between two area. It is explained by the fact that only a few drops are enough to obtain a visible colour. Moreover, as there are interactions between the pH indicator and the protons, the pH of the solution is affected by the presence of the pH indicator.
Figure 1: Structure of the bromocresol green in its acidic (left) and basic (middle and right) form. There are two resonance structures of the basic compound. Resonance will be seen in further chapters (organic chemistry)
Note that at pH=5.5 for example, this indicator is in its basic form even if the solution is acidic. pH indicators are thus useful to have an idea of the acidity of the solution. However, a lot of pH indicators exist and are easy to use.
pH paper
The pH paper is a paper containing several pH indicators.
Initially jellow, its colour varies with the pH of the solution, from deep red for acids to deep blue for bases. Usually one droplet of the solution is dropped on the pH paper, giving it its colour. One can next compare the colour of the pH paper with a scale on the box of the pH paper to determine the pH of the solution.
pH meter
This device determines the concentration of protons in solution thanks to an electrode plunged in the solution. It is more accurate than the two other methods but may need calibration. Its functioning will be seen later.
Chapter 2b: Strength of acids and bases
The general definition of an acid is thus a compound releasing protons. However, all the acids don’t have the same strength or acidity. We can define two types of acids and bases: Strong acids and bases, and weak acids and bases. For more simplicity, we will focus on acids in this lesson but the principle is identical for bases.
Strong acids
Strong acids totally dissociate in solution. It means that any single molecule of acid put in water will free a proton and acidify the solution. For example, HCl is a strong acid.
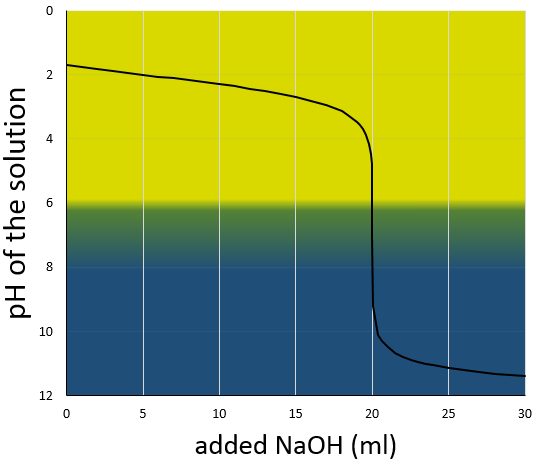
If one mole of HCl is put in water, all the HCl dissociates and in solution we can only find H2O, one mole of Cl– and one mole of H3O+. For this kind of reaction, the arrow separating reactants and products is a simple arrow going from left to right as the reaction is only going in one way. The potential Hydrogen, or pH, can thus simply be found with the quantity of HCl put in solution. pH=-log [H3O+] and as the reaction is complete, the quantity of H3O+ in solution is equal to the quantity of HCl put in solution. The concentration of protons is thus equal to the concentration of HCl in solution before the reaction [H3O+]=[HCl]0.
For example, if 0.1 mole of HCl is put in water to obtain a total volume of 1l, [H3O+]=0.1mol/l and pH=1. In lab, in general the acid is already in solution with a large concentration (6M for example) and has to be diluted to the desired concentration for the experiment. Remember that precautions are to be taken when you manipulate acids and bases, especially with concentrated ones. Use a pear to pipette them and not your mouth. Another “holy” rule is that “One does not baptise an acid”, meaning that to dilute an acid, add the acid into water and not water into the acid. The reason is that the dilution of an acid is highly exothermic and droplets of acid may be ejected out of the recipient.
The effect of a dilution on the pH is simple. If a solution of pH=2 ([H3O+]=0.01mol/l) is diluted 10 times, the pH increases by one (as it is a logarithmic scale) and pH=3 ([H3O+]=0.001mol/l), etc. For bases, a dilution decreases the pH of the solution towards the neutrality (pH=7). It is indeed the concentration of OH– which is affected in this case. As pH=-log[H3O+]=14+log[OH–].
Furthermore, a large dilution of an acid won’t lead to a basic solution. The dilution by 100 of a solution of pH=6 does not give a solution of pH=8 but approximately pH=7. In this case the water is the mean species defining the pH. The concentration of the protons coming from the acid becomes negligible with regard to the concentration of protons freed by the water.
To be considered a strong acid, the dissociation constant of the acid has to be large enough to proton all the H2O molecules of the solution into H3O+. Formally, strong acids have a pKa<-1.74. Lets explain that. We have seen that water has a dissociation constant of Kw=10-14mol2l-2. The dissociation constant of an acid is noted Ka. The same way as pH is –log of the proton concentration, pKa=-log Ka. For example HBr has a pKa of -8.7. The limit of pKa<-1.74 is simply the concentration of the water:
In 1l of water there is 1kg of H2O. The molar mass of H2O being equal to 18.01528g, the concentration of pure water is [H2O]=55.5084. –log of this concentration is 1.74.
To resume, to be able to proton all the molecules of water of the solution, which is the condition to be considered a strong acid, the acid has to have a pKa<-1.74. Some acids widely used are usually considered as strong acids but don’t answer to this condition but are between 0>pKa>-1.74 because they fully dissolve in diluted solution. These are the almost strong acids.
Among strong acids, we can find hydrochloric acid (HCl, almost strong acid), sulphuric acid (H2SO4), nitric acid (HNO3, almost strong acid), hydroiodic acid (HI), percloric acid (HClO4), hydrobromic acid (HBr) and many other.
Examples of strong bases: Sodium hydroxide (NaOH), Potassium hydroxide (KOH), Calcium hydroxide (Ca(OH)2),…
The conjugate base of strong acids are very weak bases and are inert as a base. Indeed, the basicity of the conjugate base of an acid (and inversely) is related to the Ka of the acid. The relation is Ka.Kb=Kw=10-14. Imagine for a second that the conjugate base reacts with water. If we add the reactions of the acid and of its conjugate base, we obtain the autoprotolyse of water:
HCl has a Ka=103 and the Kb of Cl– is thus Kb=10-17.
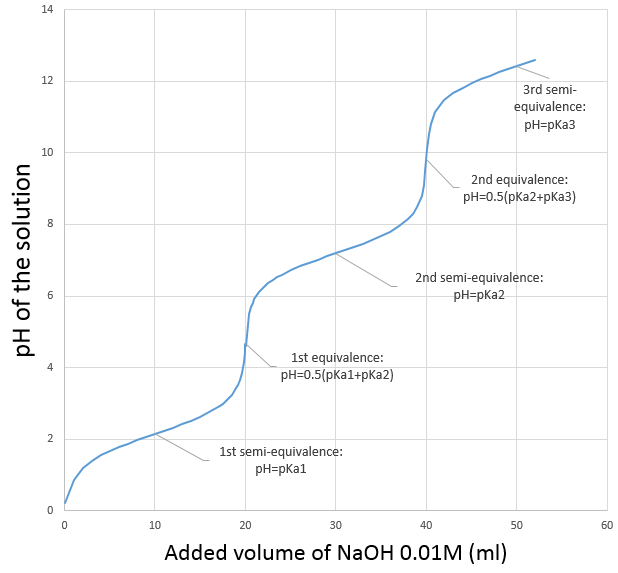
Weak acids
The acids do not all completely dissolve in water. Acids with pKa>0 are considered as weak acids. Because all of the molecules of acid do not dissolve, there is an equilibrium between the dissociated and the undissociated forms of the acid.
The equilibrium is represented by the two arrows between reactants and products.
An example of weak acid is the acetic acid (CH3COOH).
In solution, there is thus a melange of those 4 molecules. The pH is still determined by the amount of protons in solution. How do we find this quantity in the case of weak acids?
The constant of reaction of this reaction is
Lets take a look at the concentration of the species before and after the reaction
One part of the initial concentration of the acid (Ca) has reacted. The quantity of protons and of the conjugate base (CH3COO–) produced after the reaction are equal.
Generally, Ca>>[H+] (be carefull with this approximation for diluted solutions), leading to the following relation.
The pH of the solution can thus be found from the initial concentration of the acid put in solution and from its Ka:
For bases, the relation is similar:
Those relation can also be written as
From those equations, one can directly see why this kind of acid is weak with regard to strong acids: To obtain an increase of the pH of 1, a strong acid is diluted by 10 while a weak acid has to be diluted by 100.
Contrarily to strong acids, the conjugate bases of weak acids are active as a base in the solution. For example, the conjugate base of a weak acid with Ka=10-4 has a Kb=10-10.
Factors influencing the acidity
Electronegativity: The electronegativity refers to the ability of atoms to keep its electrons and the electrons of the bonds he shares near its nucleus. For two bonded atoms of same electronegativity, electrons composing the bond are not static but they spend an equal time at each end of the bond (statistically). For two bonded atoms of different electronegativity, electrons spend more time in the vicinity of the atom of larger electronegativity. This generates a separation of charges, a dipole with a partial negative charge (noted δ–) on the electronegative element and a partial positive charge (noted δ+) on the electropositive element. In acids, H possesses a partial positive charge depending on the electronegativity of the atom he is bonded to.
This partial positive charge stimulates the dissociation of H and thus increases the acidity of the molecule. Taking a look to the Mendeleev table, moving from left to right across a row on the periodic table elements become more electronegative (excluding the noble gases), and the strength of the acid formed by the element and hydrogen atoms increases accordingly.
Electronegative elements that are not directly bonded to the hydrogen can also pull electrons from the hydrogen. The effect is way smaller but should not be neglected.
Radius: Larger atoms have their bonding electrons further from the nucleus than small atoms. Because of this distance, these electrons are less energetic: there is a smaller interaction with the nucleus and the charge of the nucleus is partially shielded by the electrons of the inner layers. As a consequence, the bond is more easily broken to release a proton if the atom wearing the Hydrogen is large. The sequence of acidity for the halogenous acids shows it clearly. Hydrofluorous acid HF is a weak acid (pKa=3.2) and is less acid than HCl, HBr or HI even if its electronegativity is larger than theirs because it is much smaller (by a factor 2 to 3). The bond between the fluorine and the hydrogen is thus stronger because electrons are close to the nucleus. HI is the largest of the sequence and is also the most acidic halogenous acid with a pKa of -9.3>pKaHBr (-8.7)>pKaHCl (-6.3))>> pKaHF (3.2). Moving down a column on the Mendeleev table, the size of the elements increases and become less electronegative. The size effect tends to dominate the variation of electronegativity and the acidity increases of compounds wearing Hydrogens atoms.
Polyacids
Earlier, we mentioned the sulphuric acid, H2SO4. This acid has two protons available.
H2SO4 is a strong acid (pKa1=-3). When sulphuric acid is put in solution, a first proton is freed and there should be no remaining H2SO4 in solution. On the other hand, HSO4– is a weak acid (pKa2=1.9) and it will not totally dissociate in water. To determine the pH, we can proceed as we did for the weak acid:
With simple math, one can see that [HSO4–]= 2Ca- [H3O+] and we can write
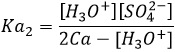
From that point, we obtain a second degree equation
![]()
That has now to be solved to obtain
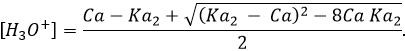
The pH can still be calculated from the constant of dissociation and from the initial concentration of acid put in solution even if the solution is a bit more difficult.
Amphoteric species
Amphoteric species are species who show both acidic and basic characteristics. HCO3– is an example of amphoteric species. As for the sulphuric acid, H2CO3 is a polyacid. However the carbonic acid is a weak acid and there is thus an equilibrium involving HCO3– as the conjugate base of H2CO3.
Water is also an amphoteric species as it can free or accept a proton.
There is a particular pH at which the amphoteric species has the same effect as a base than as an acid. This pH is called the isoelectric pH or pI. For H2O, the isoelectric pH is 7 but it can be determined from the value of Ka:
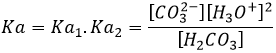
Considering that [H2CO3]=[ CO32-] at this pH,
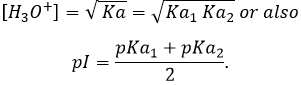
Amino acid is another amphoteric species. Such kind of molecule wears an acid group and a basic group. Fig.1 shows the structure of an amino acid in its acidic (left), neutral (middle) and basic form (right). The acid group of the amino acid is the COOH group. Its hydrogen atom can be released to obtain a negative charge on the oxygen. This charge is stabilised by resonance by the COO– group. The amine group on the left of the molecule has the role of the base. The azote possess a pair of electrons available to accept a proton.

This amphoteric property of the amino acid is used experimentally to separate amino acids between them. Because of their particular structure (R varies depending on the amino acid), each amino acid has a different isoelectric pH. The molecules are placed on a gel containing a gradient of pH, inside an electric field. As long as the amino acid is not in its neutral form, it is attracted by an electrode placed at an extremity of the gel. Each amino acid will thus stop to move at a different place on the gel and can be separated. For example Alanine (R=CH3) has a pI=6 while pI=5.48 for the phenylalanine (R=CH2C6H5).
Exercices
You can find here a few exercices to apply the theory explained in this section and eventually sections related to its subject. Most of the questions should be simple to answer but some may require a calculator, or be thougher. Answers are given underneath.
- What is the pH of a solution of HCl 0.5M?
- How do I procede experimentally to obtain 100ml of HCl 0.05M?
- What is the pH of this solution?
- If I put a droplet of this solution on a bit of pH paper, what color does the paper take?
- Is HClO (Cl-O-H) an acid or a base?
- What is the pH of a solution of HClO 0.025M (pKa=7.497)?
- If this solution is diluted by 10, what is its pH? and if diluted by another 10?
- What is the pH of a solution of NaOH 0.01M? of NH3 0.01M (Kb=1.8×10−5)? At the equilibrium, how much NH3 remains in solution?
Answers:
- pH=0.3: HCl is a strong acid and completely dissociates in solution. pH=-log[H3O+]=-log[HCl]=0.3
- Even if the acid is not very concentrated in this case, it still has a high pH and precautions have to be taken to manipulate such a solution. Here, we just need to do a dilution of the acid solution by 10. To obtain 100ml of diluted solution, we will need a pipette of 10ml and its pear, and a volumetric flask of 100ml. One does not baptise an acid. The flask is thus first filled with a volume water (50ml for example) and 10ml of the acid solution is added using the pipette and its pear. Avoid to use your mouth. Mix the solution and add water to the graduation. Mix one more time.
- pH=1.3: As the initial solution has been diluted by 10, pH increases by 1. No need to calculate here.
- Deep red
- HClO is an acid: it was fully explained in the previous section: in HClO (Cl-O-H), the electronegativity difference between Cl-O is larger than the one between O-H. The hypochlorous acid splits in ClO– and H+. χ–Cl=3.16, χ–H=2.2, χ–O=3.44
- pH=4.55. The hypochlorous acid is a weak acid. The pH formula is then
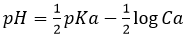
- pH=5.05 for a dilution by 10 and 5.55 for a dilution by 100.
- NaOH: pH=12, NH3: pH=10.63, [NH3]=0.009576M. We can here simply use the formula of weak bases for NH3 (remember that the pKa+pKb=pKe) but we will need the details for the third part of the question, so lets develop the problem:
Considering that Cb>>[OH–], and we will see that this approximation is correct, we find
So from the 0.01M of NH3 that were put in solution, only ~4% dissociate. The remaining concentration of NH3 is [NH3]=0.009576M. pH is found using pH=14+pOH=10.63.
Chapter 2c: Neutralization and titration
Neutralization
A neutralization reaction is the reaction occurring between an acid and a base forming a salt and water.
Technically, the neutralisation is not a one step reaction in the sense that all the actions are not done simultaneously but step by step. The fist step is the dissociation of the acid and base from their conjugate species. The second step is the formation of the salt from the conjugate species and of water from H3O+ and OH–. For example, NaOH is neutralised by HCl to form NaCl (cooking salt) and water.
The first equation is indeed the addition of the 4 equations underneath. If a compound is found at both sides of the equation, as the ionic species, we don’t write them in the mean equation. Note that all the molecules of Na+ and Cl–
are not reacting to give NaCl. There is here an equilibrium between the species in solution and the salt precipitating. This equilibrium is to be seen in the section of Dissolution.
The neutralization point is reached when the quantity of acid and base put in solution are equal. All the reactants are then consumed and for this reaction the pH is neutral, i.e. pH=7.
Titration of strong acids/bases
Titration is a method used to determine the concentration of a compound through its neutralisation. For example, the concentration of a solution of HCl can be determined by the addition of a solution of NaOH. The concentration of the titrating solution is known. As we are in presence of a strong acid (HCl) and a strong base (NaOH), both of them completely dissociate in solution. The concentration of proton is initially equivalent to the concentration of Cl–. In the other solution, the concentration of OH– and of Na+ is equivalent of the known concentration of NaOH.
To obtain a neutral pH, the number of protons na (in moles) has to be equal to the number of OH–, nb (in moles). In other words, neutralisation, or equivalence, is reached when
The number of moles of a compound in a solution is simply the concentration of this species multiplied by the volume of the solution:
From the two previous relations, we can find the initial concentration of acid that we wanted to determine:
As an example, if 20ml of NaOH 0.01M was required to neutralise a volume of 10ml of the HCl solution, [HCl]=0.02M.
In laboratory, titrations are performed as follow:
A flask containing a given volume of the unknown solution is placed on a magnetic mixer. The magnetic chip is placed in the solution to mix it continuously during the experiment. To be able to observe the neutralisation process, two droplets of pH indicator are added to the solution. Several indicators can be used to observe the passage through pH=7. Here, we will use bromothymol blue the color of which changes from yellow (pH<6.0) to blue (pH>7.6). At pH=7, the color is green. Considering the previous example, our solution is thus yellow. We can already say that the solution is acidic and that its pH is smaller than 6.
The neutralising solution, NaOH 0.01M in our case, fills a burette placed a few centimetres above the other solution. There is no need to add color indicator in this solution. Manipulating carefully the burette, NaOH is slowly added to the acid solution. One can read the consumed volume of base on graduations of the burette. When pH approaches 6, one can see the base droplets turning blue while mixing in the solution. Not knowing at all the concentration of the acid, it is convenient to perform a fast experiment to determine an approximate volume for the neutralisation and to perform a second experiment, only going slowly at the approach of this volume. Typically, the color will change from yellow to green or directly to blue at the fall of one droplet. The precision of this experiment is thus limited to the precision of the burette. Generally, the volume of a droplet is the half of a graduation.
The titration curve of this example is shown next.
Remember that the pH is the logarithm of the concentration of protons while the addition of the base is linear, and that the volume of solution increases with the addition of the base (don’t forget that point when choosing the volume of the flask). As we can see, the pH variation is mainly focused at the vicinity of the neutralisation point. At 20ml, pH=7 but at 19.95ml (one less droplet approximately, for a 50ml burette), pH=4.78 and at 20.05ml, pH=9.22.
We can also find the equivalence point by tracing the tangents of the curve in the acid region and in the base region. Those two tangents are parallel. When we trace the line equidistant to those two line, it meets the equivalence point.
Titration of weak acids/bases
The titration of a weak acid is done using a strong base and follows the same principle. Lets perform the titration of the acetic acid. The reaction is
This reaction is complete. Before the titration, the pH of the acetic acid solution is simply given by the relation for a weak acid saw in the previous section
As for the strong acids, the equivalence is reached when
However, the pH at the equivalence is not neutral but basic. Indeed, the conjugate species of a strong base/acid is inert but the conjugate species of a weak acid/base is itself a weak base/acid: pKa + pKb = 14. All the acetic acid and NaOH are consumed but acetate has been produced and it is a weak base.
Before the equivalence, the pH depends on the quantity of weak acid and of its conjugate base:
This melange between a weak acid and its conjugate base is called a buffer solution because the addition of a strong base or acid does not modify sensibly the pH of the solution. Buffer solutions are very important for living species to resist to sudden variations of the environment. An example of buffer solution is our stomach. No matter what we eat or drink, its pH is unaffected (approximatively) so that the job can be done. In our whole body, enzymes are effective in a given area of pH and to keep them working, the pH has to be regulated through buffer solutions.
The semi-equivalence is the point when there is as much CH3COOH that CH3COO–(Ca=Cb). At this point, pH=pKa. To reach the semi-equivalence point, the added volume of base is the half of the volume to obtain the equivalence.
At the equivalence, pH is given by the amount of acetate in the solution (formula for a weak base). This amount is equal to the one of NaOH added to the solution.
After the equivalence point, pH is given by the quantity of NaOH in the solution.
Titration of a polyacid
Considering a polyacid HnA (a concrete example will be given later) with different enough pKa’s, the neutralizations of the different forms of the acid are successive: The OH– will first neutralize the protons released by HnA and then the protons released by Hn-1A–, etc.
The initial pH of the solution is the pH of HnA. The concentrations of the subsequent acids are negligible. HnA may be a strong acid or a weak acid.
At the first equivalence point, Hn-1A– is the main species in solution. It is an amphoteric species, i.e. it can accept or donate protons. The pH is thus
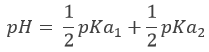
At the next semi-equivalence point, [Hn-1A–]=[ Hn-2A2-] and we are in a buffer solution. Remember that the pH in buffer solutions is
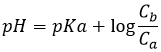
The pH is thus pH=pKa2. Note that if the initial acid is a weak acid, the same is true for the first semi-equivalence point, i.e. pH=pKa1.
It is interesting to note that for those specific values, pH does not depend on concentrations.
Let’s take the case of H3PO4 as an example. Its pKa’s are very different from each other
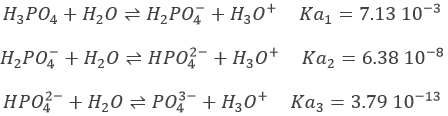
The neutralisations are successive and we can thus find the specific points (semi-equivalences and equivalences) determined above.
H3PO4 is a weak acid. The initial pH of the solution is thus
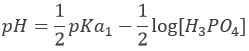
Before the equivalence, H3PO4 and H2PO4– are in solution. This buffer solution has a pH of
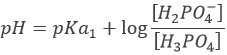
With pH=pKa1 when [H3PO4]=[H2PO4–], at the semi-equivalence.
At the first equivalence, H2PO4– is the main species in solution. It is an amphoteric species and the pH is thus
After the first equivalence, H2PO4– and HPO42- are in solution. This is again a buffer solution.
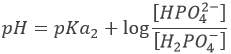
With pH=pKa2 when [H2PO4–]=[HPO42-], i.e. at the second semi-equivalence. At the second equivalence point, HPO42- is the main species in solution and is amphoteric.
After this equivalence, the solution is again a buffer solution.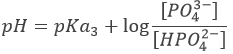
With pH=pKa3 when [HPO42-]=[PO43-], i.e. at the third semi-equivalence.
At the third equivalence, PO43- is the main species in solution. This is not an amphoteric species but a weak base. The pH should be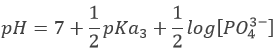
However, Ka3 is very close to Kw. Protons released by water are in competition with protons from HPO42- and the prediction does not stand anymore. To calculate the pH, we need to go back to the full composition of the solution and then solve the equation. This will not be done here.
Exercices
- What is the color of bromothymol blue in a 20ml solution of NaOH 0.005M? If we add 10ml, 20ml or 30ml of HCl 0.005M?
- What is the color of bromothymol blue in a 20ml solution of H3PO4 0.1M? If we add 10ml, 20ml or 30ml of NaOH 0.1M?
Answers
- 0ml: blue (pH=11.7), 10ml: blue (pH=11.22), 20ml: green (pH=7), 30ml: jellow (pH=3).
- 0ml: jellow (pH=1.57), 10ml: jellow (pH=pKa1=2.147), 20ml: jellow (pH=4.67), 30ml: green (pH=pKa2=7.2).
Chapter 3a: Organic chemistry, structure and names of alkanes
Organic chemistry is the chemistry of carbon and its compounds. Carbon is one element of the Mendeleev table among many others, so why is there a complete section of chemistry related to this particular element? Carbon has a valence of 4 and can thus bind with up to 4 other elements of the periodic table. To that point there is nothing extraordinary. However, where in the inorganic chemistry atoms can only bind together to form small molecules, carbon based molecules can form long and stable chains with a rich variety of functional groups.
Organic chemistry is so called because carbon is the essential constituent of living species: proteins, ADN, lipids, sugars or fats are a few example of organic compounds, made of a structure of carbon wearing functional groups allowing them to interact together, becoming more than just their simple addition but to form a functionning macrosystem where each molecule has a specific role to sustain a stable living body.
Organic chemistry is thus very important in the science of the living, but is not limited to that. Plastic is an organic compound that we find everywhere, oil, toothpaste, shampoos, clothes, deodorants, etc. are products of organic chemistry.
To adventure ourselves in this vast world that is organic chemistry, we will first discuss over alkanes, their structures and how scientists call them, and how they are represented. Later we will introduce the different functional groups that we can find on organic compounds and finally how organic compounds react, how we can produce them or modify them.
Alkanes
Alkanes are compounds only composed of carbon and hydrogen atoms. Hydrogen has a valence of 1, meaning that it can only make one liaison with another atom. A single carbon will thus bind with 4 hydrogen to form a neutral species CH4. This molecule is called methane and is a gas in normal conditions. The liaisons are covalent liaisons. The carbon is slightly more electronegative than the hydrogen but it is not important at this moment of the lesson. Just remember that CH4 will not dissociate from a proton and is not an acid.
There are several ways to represent this molecule. The fully developed representation is as follows:
In this representation of the methane, all the liaisons are shown by a full line connecting the atoms. All the atoms are shown independently as well. This representation is in two dimensions and the hydrogen atoms in 3D are in reality not on a single plane. The structure of lowest energy is the structure where the hydrogen’s are the most separated from each other. Indeed, hydrogen’ss have a given volume and are repelling each other. To obtain that structure, an angle of 109.5° separates the liaisons. It leads to a tetrahedric structure.
Most of the time, there is no point in showing the complicated structure of large molecules. It would only make it harder to see the important information of the molecule. However, it is sometime important to know in which direction goes one particular liaison. In this case, the lines representing the liaisons take different forms depending on their orientation. In the plane of the page, liaisons are still represented by a simple line. Two other cases are possible: Liaisons can go in the direction of the reader or in the opposite direction. Liaisons going toward the reader are represented by a black triangle one peak of which is connected to the atom on the plane of the page and the two other points are connected to the atom out of the plane. This way, the triangle looks like a line going wider from the atom in the plane to the atom closer to the reader.
For liaisons going in the opposite direction, atoms are connected by traits (parallel or perpendicular to the liaison direction your choice). For methane, it gives the following 3D representation:
The alkane possessing a structure of 2 carbon atoms is the ethane. It is a gas as the methane. To form the “bone” structure of the ethane, the two carbon atoms bind together through a covalent liaison. Obviously they have the same electronegativity. From their 4 electrons, one is thus used by each carbon to bind with the other one. 6 hydrogen will thus complete the structure. As in inorganic chemistry, the octet rule is respected: to be stable, a carbon has to have 8 electrons (an octet) around it: its 4 electrons and 4 electrons of the other atoms with which it shares a bond. Each carbon of the ethane is thus bound with a carbon and with 3 hydrogens. It is the single possible structure for such compound. In no way one carbon would wear 5 hydrogens and the other carbon 1 or more.
The fully represented structure of the ethane is thus
If we want to represent it in 3D, it would be:
However, it is to be said that atoms can rotate in the axe of a simple liaison. The 6 hydrogen are thus turning in circle around the axis made by the two carbons, as shown above. The Hydrogen’s are rotating almost freely around this axis.
Each hydrogen has a given volume and feels the atoms in its vicinity (steric hindrance). When rotating, the distance between hydrogen’s on a same carbon is constant. However, the distance with the closest hydrogen carried by the other carbon changes.
The relative positions of substituents can be showed through the Newman projection. The molecule is observed along its C-C axis. The first C (proximal carbon) is represented by a circle from the centre of which three lines are going out. These lines are the liaisons of this carbon. The second carbon (distal carbon) is hidden by the first one but one part of the liaison is visible.
Fixing the hydrogen’s of the proximal carbon, only the hydrogen’s of the distal carbon can move. Two cases can be observed:
- The hydrogen’s of the distal and of the proximal carbons are on the same spots, or so called eclipsed
- The hydrogen’s are not on the same spots, or so called staggered
A maximum of energy is reached in the eclipse conformation because repulsion between the hydrogen’s is maximal in this conformation. A rotation of 60° from this conformation leads to a minimum of energy, the hydrogen’s being as far away from each other as they can be. A molecule that has to maintain hydrogen’s (or substituents) eclipsed has a higher energy than a molecule of same composition with staggered hydrogen’s. The difference in energy here is not very important and the rotation is effective. During the rotation, the molecule passes more time in the staggered conformation (smaller energy). If substituents were on the molecule, the steric hindrance increases with the radius of the substituent. In some cases, the rotation can be blocked by the presence of voluminous substituents.
The semi representation of the ethane is
In this representation, the carbons are regrouped with the atoms they are wearing but not sharing. The liaisons between C and H are thus not showed in this representation. If a Hydrogen atom was replaced by a chlorine atom, for example, the half representation would be:
Adding a third carbon atom to the chain, C3H8, the propane, is still a linear alkane. The structure in triangle where each carbon binds with two other carbon exists but is not very stable. You maybe have spotted that the formula of linear alkanes has a general model: CnH2n+2. For each atom of carbon added to the first one, 2 hydrogen are to be added.
There are two ways now to add a fourth carbon to obtain a butane molecule. The chain can be extended by its extremities or by its middle. When the chain is linear, we add n- before the name of the compound. n-butane is thus
![]()
If the chain is extended by its middle, we name this compound isobutane
The iso prefix is used only for a few compound wherein a carbon wear two terminal CH3. n-butane and isobutane share the same formula C4H10 but don’t have the same structure. Such kind of compound is called an isomer of constitution. The greater the number of carbon in an alkane, the greater the number of isomers.
For a 5 carbon chain, the fifth carbon can be added at one extremity of the n-butane to obtain n-pentane, equivalently at any extremity of the isobutane (it is the same as adding the C on one CH2 of the n-butane) to obtain isopentane, or on the CH to obtain neopentane.
Names of the alkanes:
Another representation of organic molecules is the skeleton representation. In this representation, carbons and hydrogens are not shown. The liaisons between carbons are still shown as full lines and are connected together with an angle at the position of the carbon atoms. Without angle, we could not differentiate a chain of 6 carbons from a chain of 7. Generally, the angle is approximately 120° so that if a carbon is bound to three other species (other than H), each liaison is equally distant. If a carbon is bound to 4 species, the angle is 90°.
For example, the pentanes showed above are represented
This bone structure is the representation that is usually used. Only important informations are shown. The number of hydrogen on the different carbons of the bone are determined by the number of liaisons that the carbon has. It is thus pointless to show it. Moreover, this representation is faster to write and takes less space.
There is a given method to name organic compounds. An alkane as a functional group has the same name except that the -ane is replaced by -yl. For example, isobutane is also called methylpropane because a methyl is fixed at a linear chain of 3 carbons, i.e. a propane chain.
C4H9Cl is a Chlorobutane. With this name, we know the components of the compound but not its complete structure. The connectivity in the butane and between the butane and the chlorine are not known.
The rules to name a compound are
- the longest chain is the main one. However if a functional group is on one chain, the main chain has to wear it.
- tag a number to each of the carbon from one side of the main chain to the other. The carbon wearing a functional group which is the closest of an extremity has to have the smallest number.
- Next, we name the compound by writing first the groups out of the main chain, with their number as prefix, in the alphabetical order, followed by the main chain with its group.
- our examples are thus named
- If several identical functional groups are on different carbons, the prefix are separated by a , and their number is indicated by bi, tri,…
- ex: the isooctane is the 2,2,4-trimethylpentane, meaning that a total of 3 methyl groups are on a main chain of 5 carbons. Two methyls are on the carbon #2 and one on the #4. It is 2,2,4-trimethylpentane and not 2,4,4-trimethylpentane because we favor the carbon wearing more groups.
Halogenoalkanes
Simply said, halogenoalkanes are alkanes wearing one or more halogen. It is simply said but halogenoalcanes are not so easily made. They are made from a dihalogen and an alkane through a radical reaction during which a proton has to be removed from the alkane. This step of the reaction is not favorable but can be made through heavy heating (300° for the chloromethane). Also, the position of the halogen is not completely fixed. The proton removed during the reaction is easier removed from a carbon in the chain than at an extremity but the high temperature makes both positions possible (the distribution depends on the temperature)
Halogens have a higher electronegativity than C and they generate a dipole from C to X. A carbon wearing an halogen is thus poor in electrons and will consequently be targeted by reactants rich in electrons. The reactivity of halogenoalkanes will be seen in a further section.
Chiral molecules
We have already see that for one given formula, several different molecules may exist. When the connectivity differs, these are isomers of constitution.
Ex: butane and methylpropane, ethanol and methoxymethane.
Even on a single carbon, the connectivity may change. Stereoisomers are isomers of same connectivity but with different spatial positioning. The bromochlorofluoromethane has two stereoisomers forms.
These two molecules are mirror images one of the other. It is said that they are chiral if the molecule and its mirror image do not superimpose. These particular stereoisomers are called enantiomers.
A good way to explain chirality is to look at our hands. The left hand is the mirror image of the right hand (and vice versa). However, we cannot superimpose them.
Chirality is related to the carbon that wears several different groups. It is a stereocentre. Stereocentres are often indicated by an asterisc. If a plane of symetry exists for the molecule, this molecule is achiral (><chiral) and this molecule and its mirror image can superimpose somehow. For example, Bromofluoromethan is achiral because a plane of symetry can be drawn, passing by the two hydrogen atoms.
Our body is able to distinguish enantiomers from each other. For some medicines, one enantiomer is active while the other one will do absolutely nothing, or will be less effective. In some cases, it is thus very important to be able to produce selectively one enantiomer and not the other one. Pharmaceutical indrustries invested such methods. If the reaction is not enantioselective, the productivity immediately drops by 50%. The optic activity of enantiomers also differs and is a good way to know which enantiomer have been produced.
Optic activity
The optical activity of a compound is its influence on a plane polarised light beam. When the light, filtered only to oscillate in one plane, passes through a sample of an optically active compound, the beam is rotated by a given angle.
The angle of rotation depends on the molecules in the sample, of their concentrations and on the length of the sample cell. Each of these effects are linear and the modification of the angle of the light is given by the formula
The interest here is that enantiomers don’t have the same optical activity. The absolute modification of the angle is identical, but the direction in which the light is rotated is not. One enantiomer deviates the light towards the right and the other enantiomer deviates the light by the exact same angle but towards the left. The enantiomers are respectively defined as dextrogyre and levogyre and noted with a (+) or a (-).
The optical activity of an enantiomer is fixed for this molecule, at a given temperature t and for a light of given wavelength λ. Knowing its value, it is possible to determine the quantity of each enantiomer in a racemic mix/melange. A racemic melange is a solution containing the two enantiomers, not necessarily in the same quantity (nb: a more global definition of a racemic melange is the melange of several possible products of a single reaction). In such a melange, all the species will deviate the light with their normal effect.
If the two enantiomers are in equal quantities in the solution, the sample will be optically inactive, the effect on one enantiomer being counterbalanced by the effect of its specular image (i.e. the other enantiomer). If the quantities are not equal, the sample is optically active and the relative quantities of the enantiomers can be determined. The enantiomeric excess is the difference of proportion of the two enantiomers and is practically the proportion of the enantiomers that have an effect on the light. For example if the ratio between the enantiomers was 3:1 (75% of one (let’s say the dextrogyre) and 25% of the other enantiomer), the enantiomeric excess is 50%. Indeed, from the 75% of the dextrogyre enantiomer, the effect of 25% is counterbalanced by the levogyre enantiomer present in the solution. Only 50% of the (+) enantiomer deviates the light beam. If the pure enantiomer would have rotate the light plane by 26°, an entantiomeric excess of 50% rotates the light by 13° (50% of 26°).
Name of the enantiomers
We need a way to name differently the enantiomers. R or C will precede the name of the molecule and we will now see how to attribute which letter to which enantiomer. It is unfortunate but there is no clear correlation between the optic activity of an enantiomer and its structure. Another method had to be find.
The first step is to give a priority to each group attached to a stereocentre.
Priority is given in regard with the mass of the atom directly bound to the stereocentre. Let’s name these groups a,b,c and d by decreased priority (A priors to B, B priors to C, C priors to D). If two atoms have the same weight (two carbon are bound to the stereocentre for example), we look at the atoms they are wearing and, again, the priority goes to the carbon wearing the atom of larger atomic weight. If a methyl and an ethyl were bound to the stereocentre, the ethyl has the priority. Both groups are bound to the stereocentre by a carbon atom. We look now at the atoms on these carbons. The methyl has 3H and ethyl has 2H and one C. As C is heavier than H, the ethyl has the priority on the methyl.
Remember that it is the weight of the bound atom that matters, not the weight of the complete group. A –OH groups has indeed the priority on an ethyl group because O (atomic weight=16) is larger than C (12) even if the groups weight respectively 17 and 29 units of atomic mass. Note that we are talking about the mass of the elements. Isotopes can thus create stereocentres in molecules.
Next, we look at the molecule as if the group with the lowest priority (D) was behind the carbon. Generally the group with the smallest priority is a Hydrogen atom. This atom (or group) is not represented in the rest of the method.
So, looking at the stereocentre this way, we only see 3 liaisons connecting the stereocentre with the three groups of highest priority (A, B, C).
Now, we want to determine in which sense to rotate to go from the highest priority (A) to the lowest (C), passing by B. It may be helpful to place A in top of the representation.
If we must go clockwise, it is the enantiomer R. If it is counterclockwise, we are in presence of the enantiomer S.
A second method exist, giving the same results, using the Fisher projection.
Instead of placing a group behind the stereocentre, we put two groups horizontally and two group vertically, still by a rotation of the stereocentre. The horizontally oriented groups are pointing toward the reader. The other two groups that are on the vertical axis are pointing opposite to the reader.
The rotation of the stereocentre is done by “grabbing” a pair or substituents and placing them in front of the molecule. Be careful to place the horizontal groups in the direction of the reader and the vertical ones in the opposite direction. Otherwise, a R enantiomer becomes S and vice versa.
Once the rotation is done, to determine the correct configuration, the group of lowest priority has to be placed on the 12 o’clock position of the Fisher representation. Then, the configuration is determined the same way as for the Newman projection. If the lowest priority group was not in the top position after the rotation, don’t worry, we can perform permutations between near substituents. Performing one permutation changes the conformation of the enantiomer from R to S and vice versa. Performing two let the enantiomer identical.
If an even number of permutations (including zero) were done to put the lowest priority group in the 12 o’clock position, we can determine directly the configuration of the enantiomer. If an odd number of permutation was done, then you have two choices: either you determine the present configuration, knowing that the correct configuration is the other one, or you do one additional permutation and then determine the configuration.
Diastereoisomers
Several stereocentres may be present on a single molecule. The configuration of each stereocentre (R or S) is determined independently. If two stereocentres are on one molecule, several configurations are possible: RR, SS, RS and SR.
For example, 2-Bromo-3-chlorobutane has 4 stereoisomers.
All those conformations are not mirror image of each other. Some stereoisomers are enantiomers but some are not. Stereoisomers that are not the mirror image of each other are called diastereoisomer.
Exercises:
- Draw the skeleton structures of the isomers for C8H18. How many isomers did you find?
- Name the following molecules:
3. Draw the following molecule:
- 3,6,10-trimethyldodecane
- 5-ethyl-2-methyloctane
- 2,6-dimethyl-4,5-dipropylnonane
- 4-(1-methylethyl)heptane
- Is this name correct? If not, correct it.
- 2,5-dimethyl-4,6-dipropylnonane
- 3-ethyl-7-methyloctane
- 2,5-dimethyl-4-ethyldecane
- 4-(1-methylethyl)-5-propyldecane
- Draw the Newman projections of the C-C liaisons of this molecule and write if they are eclipsed or staggered
6. Chiral or achiral? If chiral, indicate if they are R or S.
Answers
1. There are 23 isomers of constitution for C8H18. A good way to find them all is to start from the longest main chain and decrease its length step by step.
2. Names:
2.1 n-hexane
2.2 Neopentane or 2,2-dimethylpropane
2.3 4-ethyl-7-methyldecane. It is not 4-methyl-7-ethyldecane because substituents are placed in alphabetical order if at the same distance from one extremity of the chain
2.4 6-propyl-3-methyldecane (main chain from top to bottom right)
2.5 5-(1-methylpropyl)decane
2.6 4-ethyl-4-methyloctane
3. Names and sketch:
3.1. 3,6,10-trimethyldodecane
3.2. 5-ethyl-2-methyloctane
3.3. 2,6-dimethyl-4,5-dipropylnonane
3.4. 4-(1-methylethyl)heptane
4. Correct or not?
- 2,5-dimethyl-4,6-dipropylnonane: correct
- 3-ethyl-7-methyloctane: incorrect: the methyl substituent is closer of an extremity than the ethyl. The correct name is 6-ethyl-2-methyloctane
- 2,5-dimethyl-4-ethyldecane: incorrect: substituents have to be named in the alphabetical order. The correct name is 4-ethyl-2,5-dimethyldecane
- 4-(1-methylethyl)-5-propyldecane: correct
5. Newman projections going from left to right
6. Chirality:
6.1 Chiral: R
6.2 Achiral
6.3 Chiral: S
6.4 Achiral
6.5 Chiral: S
Chapter 3b: cycloalkanes
Cycloalkanes
A cycloalkane is, as it name shows, a cyclic alkane chain. Each carbon of the chain is bound to (at least) two carbons and two hydrogen’s. The general formula is thus CnH2n and the name of the compound is the same name as the corresponding alkane with the prefix cyclo.
Cyclopropane
The smallest cycle, cyclopropane, is made of 3 carbons. Each carbon is bound to the two others with a triangle shape.
That means that the carbons are in the same plane and that the angle between liaisons is 60°. This angle is far from the normal angle between liaisons in alkanes. Remember that carbons have a tetrahedral structure with an angle of 109.5° between each liaison. To be cyclic, there is a deformation of the carbon structure and a tension of cycle is maintained. It is possible to determine the importance of this tension from the energy of combustion ΔH°comb of the cycloalkane.
For a linear alkane, the heat of combustion increases by approximately 658.5kJ/mol when the length of the chain is increases by one unit. One can conclude that the average ΔH°comb of a CH2 is 658.5kJ/mol. Applying this to the cyclopropane, C3H6, the calculated ΔH°comb is -1975.5kJ/mol. However, when we experimentally perform the combustion, we find that ΔH°comb =-2091.2kJ/mol.
The cyclopropane releases thus more heat than what we could expect. The difference, 115.7kJ/mol (38.6kJ/mol/CH2), comes from the cycle tension, i.e. the molecule requires more energy just to bind this way. In fact, the orbitals of the carbon are not well aligned but the angle between orbitals is 104°.
As a result, the liaisons are weak and cyclopropane is not very stable. It is indeed easily open through catalytic hydrogenation.
Finally, the position of the hydrogen atoms is unfavourable. Let’s have a quick reminder at the eclipsed and staggered conformations for the hydrogen’s in ethane (C2H6). Hydrogen’s can rotate around the axe formed by the liaison C-C. Each hydrogen has a given volume and feels the atoms in its vicinity (steric hindrance). When rotating, for a given H the distance with the closest hydrogen carried by the other carbon changes.
On the Newman projection,
- the hydrogen’s are on the same spots, or so called eclipsed
- the hydrogen’s are not on the same spots, or so called staggered
A maximum of energy is reached in the eclipse conformation because repulsion between the hydrogen’s is maximal in this conformation. Cyclopropane has to maintain its hydrogen’s (or its substituents) eclipsed and it requires a lot of energy to the molecule. In the cyclopropane, all the hydrogen’s are eclipsed. The difference of energy between the eclipsed and the staggered conformations can be significant as we will see for cycles of more than 3 carbons.
Cyclobutane
Performing the combustion experiment on cyclobutane, for which the angles are of ~90°, we find an excess of 110.3kJ/mol (27.6kJ/mol/CH2) due to the cycle tension. It is less than for the cyclopropane because the forced bending is smaller in the cyclobutane than in the cyclopropane. The tension for these two cycles are very important. For larger cycles the tension decreases significantly and is at its minimum for a cycle of 6 carbons, the cyclohexane.
Cycles with more than 3 carbons are not plane. In the cyclobutane, the angle between the fourth carbon of the molecule, out of the plane, and the plane formed by the three other carbons is 26°.
The angle between the carbons is 88.5°. It is slightly less than for a square (90°) in one single plane. So why is the cyclobutane not plane? It should indeed decrease the cycle tension. However, in the plane conformation the 8 Hydrogen’s would be eclipsed. The 26° shaping of the cyclobutane moves the Hydrogen’s out of the eclipsed conformation. The small angle difference is thus counterbalanced by the improvement of the positioning of the Hydrogen’s.
The structure of the cyclobutane is oscillating quickly between two conformers: the carbon out of the plane moves from one side of the plane to the other. These two conformations are equivalent in energy. Looking at the next figure, 4 H are represented.
Two of them (going upwards) are pretty close from each other while the two other are distant. After the oscillation, the roles are inverted and the two Hydrogen’s have in average the same steric hindrance, also called transannular tension in this case.
Cycles can thus oscillate between several conformations when the conformations have a similar potential energy and if the energetic barrier between to switch of conformation is small enough. In the case of the cyclobutane the hindrance is very small, but if one of those 4 hydrogen’s was a substituent, the two conformers are no more equivalent. Indeed, the molecule will place itself in the most favorable conformation which is when the voluminous substituent is not affected by the transannular tension. The proportion of the conformers is no more 50:50.
Cyclopentane
The disfavour of the Hydrogen’s in ecliptic conformations is clear in the pentane. In a regular pentagon, the angle is 108°. It is almost the normal angle for a tetrahedral carbon (109.5°). However, 10 Hydrogen’s would be eclipsing one each other. The cyclopentane, and in fact any cycloalkane except the cyclopropane, is not plane. Two conformations (each with two conformers) are possible: the envelope and the semi-chair.
In the envelop conformation, 4 carbons are in the same plane, with an angle of 104.4°. In the other conformation (semi-chair), the angles are smaller but the eclipsing effect is smaller as well. The two conformations have very near potential energies and the barriers to switch between two forms are easily passed through. Cyclopentane oscillates then quickly between its conformers.
Cyclohexane
The case of the cyclohexane is particular. When we look at the heat of combustion of this species, the experimental value is less than one (0.8) kJ/mol different from the calculated one based on the number of CH2 in the molecule. Cyclohexane is the most stable existing cycloalkane.
Two conformations exist but one is more stable than the other one.
The most stable conformation is the chair conformation.
In this conformation, 2 pairs of carbons are in the same plane and the last 2 carbons are in each side of the plane. This position is called chair: the 4 carbons on the plane make the seat, one plane of 3 carbon makes the back of the chair and the other makes the footrest.
The angle between carbons is 111.4°, i.e. almost the 109.5° of a normal tetrahedral carbon, and all the Hydrogen atoms are in a staggered conformation.
This structure is thus very stable. Two types of Hydrogen’s can be distinguished: the ones in the axial position and the ones in the equatorial position. 6 liaisons C-H are parallel to the axe of the molecule (axe passing in the middle of the molecule). These are the axial Hydrogen’s. The other 6 liaisons are almost perpendicular and are called equatorial.
In we reverse the chair structure (chair’s back<->footrest), equatorial hydrogen’s become the axial ones and vice versa.
To reverse the chair, cyclohexane has to go through the boat conformation, less stable by 28.9kJ/mol (the energetic barrier is 45.2kJ/mol). In this conformation, the two carbons that were out of the plane are now at the same side of it. This does not only generate a steric hindrance, but the hydrogen’s on the 4 carbons of the plane are now eclipsing each other. That explain the difference in potential energy between the boat and the chair formations.
In reality, this conformation is only a transition state. A more stable form is the crossed-boat conformation, almost identical but reducing the transannular tension. The boat conformation is thus the transition state between the two crossed-boat conformations.
We can resume the conformations as follow:
Cyclohexane in the boat conformations only exist in very small proportions with regard to the chair conformation. We will thus only focus on the chair conformation for our further analyses.
Presence of substituents on the cyclohexane
The positions of a substituent on the cyclohexane are not equivalent.
If a substituent is placed on an axial position, the steric hindrance is greater than on an equatorial position. Indeed, equatorial substituents are more spaced than axial ones which go in the same direction. This is called the 1,3-diaxial interaction. The equatorial position for a substituent is then more stable than the axial one and one conformation of the molecule is favoured. For example, if the substituent is a methyl, the difference of energy between the conformations is 7.1kJ/mol, leading to a proportion of 95:5 (equatorial/axial). Larger substituents increase furthermore the proportion of conformers.
The Newman projection can help to visualise this phenomenon. The whole molecule is represented, connecting two Newman projections together.
Several substituents may be bound to a cyclohexane. The influence on the stability of each one is, for most of the substituents, simply additive. In the case of two substituents, one will be placed in an equatorial position anyway because it requires less energy than on an equatorial spot (as we just saw for the case of a single substituent). This substituent is the biggest one to minimize the steric hindrance. The second one, smaller, is either on an axial or an equatorial spot, depending on the connectivity of the molecule. If both groups are in equatorial positions, the equilibrium is further balanced towards this conformation. If the second substituent is on an axial spot, the equilibrium moves toward the 50:50 composition, the effects of the substituents acting against one each other.
Let’s see it through some examples. As explained before, the presence of a methyl on the cyclohexane favours the equatorial conformation by 7.1 kJ/mol. The presence of a second methyl group on an equatorial spot will increase the proportion of the equatorial conformation by the same amount (7.1kJ/mol). The total energetic advantage of the equatorial conformation reaches 14.2kJ/mol and the proportion of the equatorial conformer increases furthermore towards 99:1. This conformation is also noted trans because the groups point in opposite direction. The name of this molecule is indeed trans-1,4-dimethylcyclohexane.
If the second methyl group was on an axial spot, the two conformers are equivalents (the axial methyl becomes equatorial and vice versa). The total energetic advantage of one of the conformer is indeed 7.1kJ/mol-7.1kJ/mol=0kJ/mol.
If the second group was a chlorine atom instead of a methyl group, we proceed the same way to know which conformer is favoured. A single chlorine group stabilizes the equatorial conformation by 2.2kJ/mol. If both substituents were equatorial, the total energetic advantage of the equatorial conformer is 7.1kJ/mol (from CH3) +2.2kJmol (from Cl)=9.3kJ/mol. This molecule is thus more stable than the methylcyclohexane.
If the chlorine atom was axial, the total energetic advantage of the conformer wherein the methyl is equatorial is 7.1kJ/mol-2.2kJ/mol=4.9kJ/mol. The conformer with an equatorial methyl is still more stable than the other conformer but less than the methylcyclohexane.
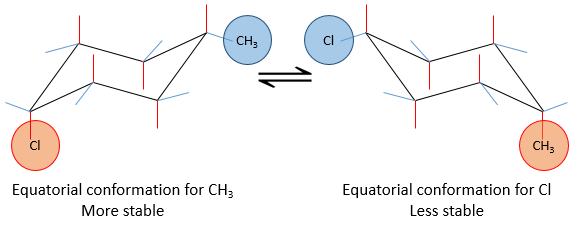
Note that other interactions may affect the stability of the conformers. When the substituents are on other spots than 1-4, interactions (as steric hindrance, repulsion,…) may decrease or increase the energetic advantage of one conformer on the other one.
Polycyclic alkanes
Molecules are not limited to one cycle. Several cycles may share carbons. A molecule composed of two hexanes sharing two carbons is called decaline and exists in a trans and a cis form. Cycles do not have to be the same size and a cyclohexane can merge with a cyclopentane.
Two cycles may also be slotted one into each other. This leads to bridged cycles. The norborane is a bridged cyclohexane or two cyclopentane sharing 3 carbons. Carbons wearing the bridge are called bridgeheads.
Polycyclic alkanes reduce the freedom of move of the molecule but it seems that there is no limit to the cycle tension that hydrocarbures can endure, as one can think from the bicyclobutane.
Polycycles with cycles of few carbons (3-4) are in general not naturally produced but may be made through synthesis. All types of carbon skeletons have been made in laboratories. They can have an interest as explosives if they wear nitro croups thanks to their important cycle tension.
Polycycles of larger cycles are often found in natural compounds, giving specific odors, parfums, colors, or very specific roles as do have hormones.