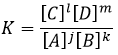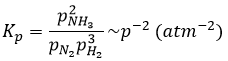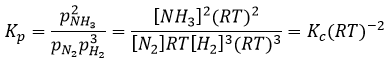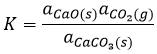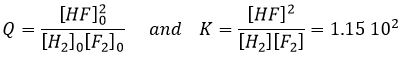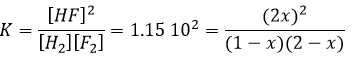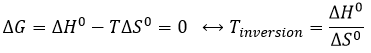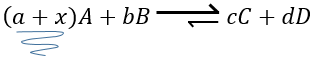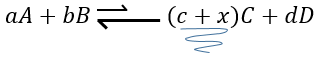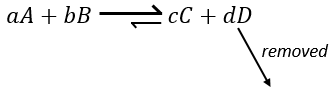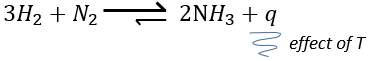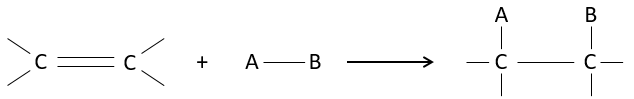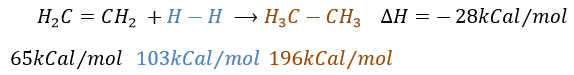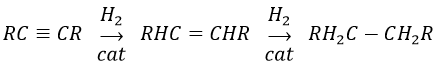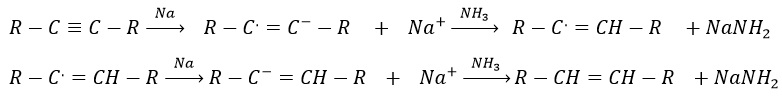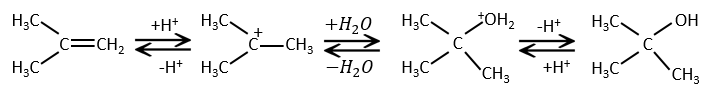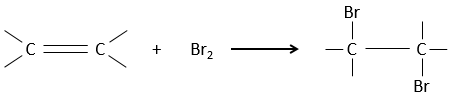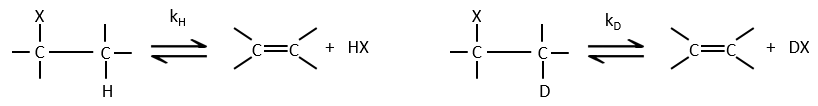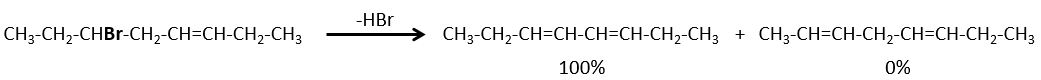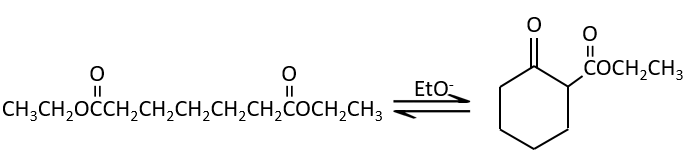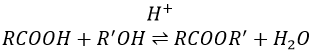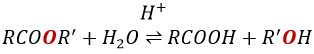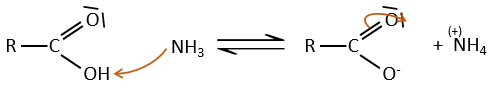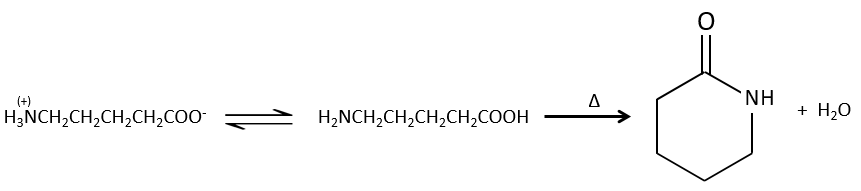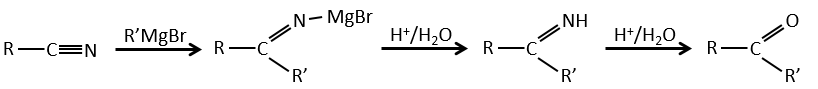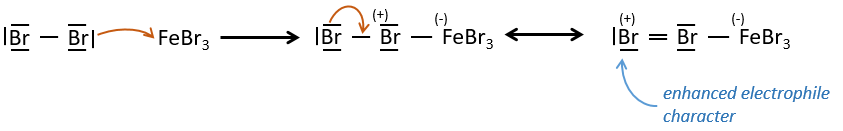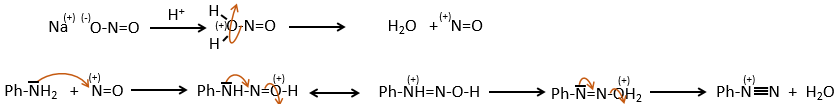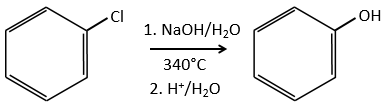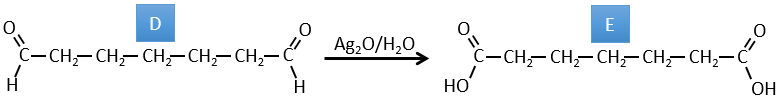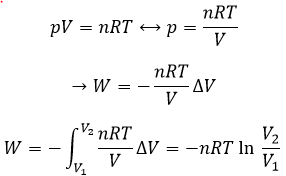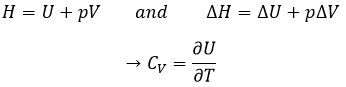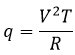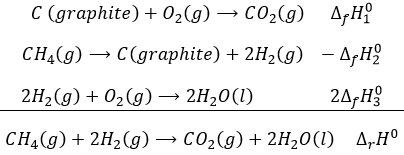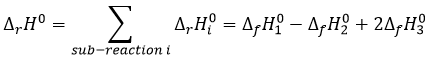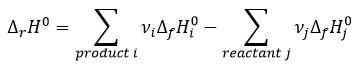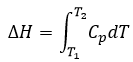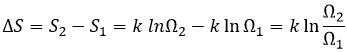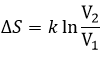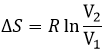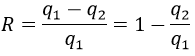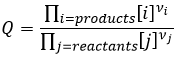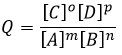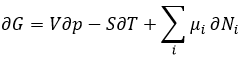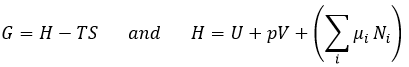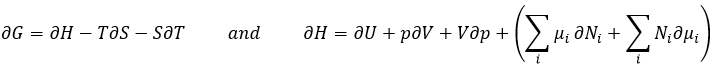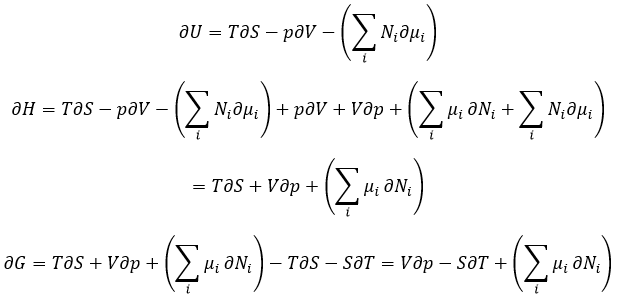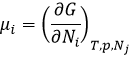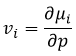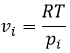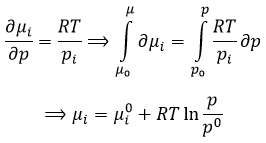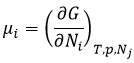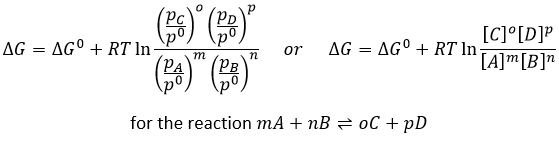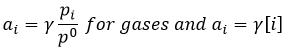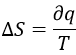Chapter 4 : Kinetics – Equilibrium
Chemical kinetics is the study of the speed of reactions. The speed of reaction is determined by the variation of the quantity of species by unit of time. Usually, we consider the concentrations for species in solution and we consider pressures for gases.
The speed of a reaction is rarely constant and is positive until the system reaches the equilibrium. At the equilibrium, the speed of reaction is zero.
Equilibrium
Given a reaction
The equilibrium is reached when the concentrations of the species don’t vary anymore over time. The constant of equilibrium K, that expresses the law of mass action, is
The constant of the reversed reaction, from right to left, is K’=1/K and if we consider a multiple n of this reaction,
K’’=Kn because stoichiometric coefficients are as exponents in the expression of the equilibrium constant.
The units of K depend of the reaction. For instance, the reaction of Haber that generates ammonia and that we already met before
has an equilibrium constant Kp that depends on the pressures of the reactants and products.
The units of K depend thus on the amount of different products and reactants and on their stoichiometric coefficients. We denoted the constant with a p because we usually consider equilibrium constants in term of concentrations, that we can denote Kc. There is a relation between Kc and Kp that we find from the law of perfect gases pV=nRT
The relation between the pressure and the concentration is thus simply a multiplication by RT. In the expression of K, this RT is also at the power of the stoichiometric coefficient.
For the reaction of Haber, we find
In the case of condensed phases, we won’t consider the concentration nor the pressure because interactions between the species have to be taken into account. We consider the activity of the species instead. The activity reflects the ability of a substrate to react. In condensed phases this ability is decreased by the interactions with the nearby molecules. The activity is proportional to the concentration of a species or to its pressure, multiplied by a coefficient γ. The equilibrium may be heterogeneous if all the species intervening in the reaction are not of the same phase. In this case too, we consider the activities of the species instead of their concentration or pressure. For instance, the reaction
is a reaction where two solids and one gas coexist. It has the following constant of equilibrium:
We choose on purpose a reaction involving solids because their activity is equal to 1. The constant is thus simply proportional to the pressure of CO2. In a closed system, this reaction won’t produce more product if we increase the quantity of reactant. The reaction is only limited by the pressure of the gas.
The reactive quotient Q
To determine the direction of a reaction, we compare the constant of equilibrium K with the reactive quotient Q. Q is determined from the initial concentrations put in presence.
For the reaction
The quotient Q and the equilibrium constant K are respectively
If we consider a system of 5l containing the following quantities of each species:
Given that there is no product in this composition, the reaction will obviously go toward the right. It is impossible to obtain negative concentrations. The reaction will proceed until it reaches the equilibrium or that all of one reactant is consumed. We can determine the concentrations of each species at the equilibrium with the following method:
We determine the concentrations of the species. Here we gave the volume of the recipient and the number of moles of each species. We write them in a table and assume that a concentration x will be consumed to reach the equilibrium. The same quantity (in stoichiometric ratios) of product has been formed.

As we know the value of K, we can determine x and thus the concentration of each species.
This equation of the second order gives two solutions but one is negative and thus impossible (no negative concentrations). We can thus determine the concentrations at equilibrium for all the species.
If K is small, for instance in the reaction
has K=1.6 10-5 mol/l, it means that the reaction does not consume a lot of reactants. If we begin the reaction with only 1 mole of NOCl(g), we will consume 0.03mol/l of it.
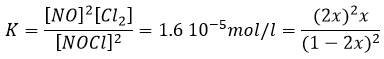
Assuming that x is small, the lower part of the fraction is simplified and
The assumption that 2x<<<1 is correct. A small equilibrium constant also means that the reverse reaction is more favourable (K’=1/K).
Temperature of inversion
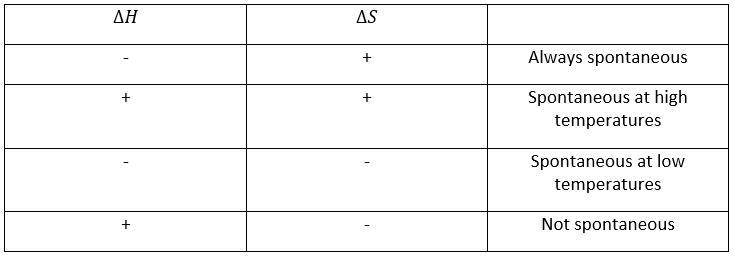
The equilibrium depends on the temperature. We have seen in the thermodynamics sections that
At a given temperature, the reactions goes in one direction but if we increase the temperature enough, the reaction will go in the opposite direction. The temperature at which it occurs is the temperature of inversion and is when
If the reaction is performed at p=1atm, we can find this temperature from the tables of ΔH0 and ΔS0:
Modification of the equilibrium
Now, if we consider a system at the equilibrium and we apply a modification on this system, Le Chatelier enounced that the equilibrium will change to counterbalance this modification.
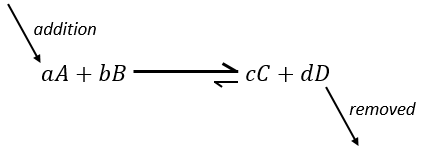
–addition of a substrate: the equilibrium will consume more of this constituent or produce less of it
For instance, let’s consider a reaction at the equilibrium
if we add more A in the system, the equilibrium is displaced to the right to consume some of the added reactant
If we added some C (a product) instead, the equilibrium would have been displaced to the left.
Another way to modify the equilibrium is to remove the products out of the system to displace the equilibrium to the right.
To optimise the speed of a reaction, we can thus add reactants and remove the products continuously.
–temperature: the equilibrium depends on the temperature, as we have seen above. The effect will be different for an exothermic reaction or an endothermic reaction. Indeed,
The variation of temperature affects the exponential with ΔH0. If ΔH0<0, i.e. it is an exothermic reaction, K decreases as result of an increase of temperature and the reaction is thus less efficient. During an exothermic reaction, heat is a product of the reaction
and the temperature increases the heat so the equilibrium is displaced to the left. If the reaction is endothermic (the reverse reaction for instance), an increases of temperature helps the reaction to proceed (more heat is available to be absorbed). The equilibrium is thus displaced to the right.
–pressure/volume: during reactions involving gases, a diminution of the volume will displace the equilibrium toward the side where there is less moles of gas. In the previous reaction, the equilibrium would be displaced toward the right because we generate 2 moles of gas from 4. We can also displace the equilibrium by the addition of an inert gas that will increase the pressure without any modification on the chemical reaction.
Experimental determination of K, ΔH0 and ΔS0
We know that the equilibrium is displaced by a modification of temperature. Imagine that we want to know the values of K, ΔH0 and ΔS0 of a dissolution process like
We know that if there is no Ag+ or Cl– in the solution before the reaction, their concentration will be equal as one of each ion is produced during the reaction. As solids have an activity a=1, the constant of dissociation Ks is
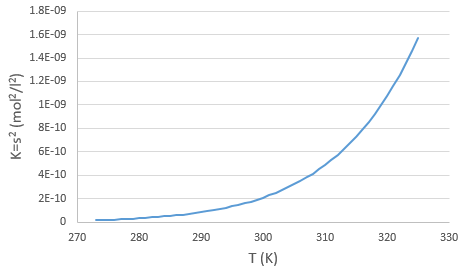
The concentration in ions is thus equal to the square root of the dissociation constant. At a given temperature, we can thus measure the concentration at the equilibrium of one of the ions to determine the value of K. We can repeat this experiment at several temperatures and plot the relation between the temperature T and K.
We see that the dissociation constant Ks increases with the temperature, meaning that if we increase the temperature, we can dissolve more AgCl in solution. AgCl is not very soluble in water: only mg of it per litre will dissolve (the square root of Ks gives the concentration). But we can find more information from this relation. We know that the equation connecting K and T:
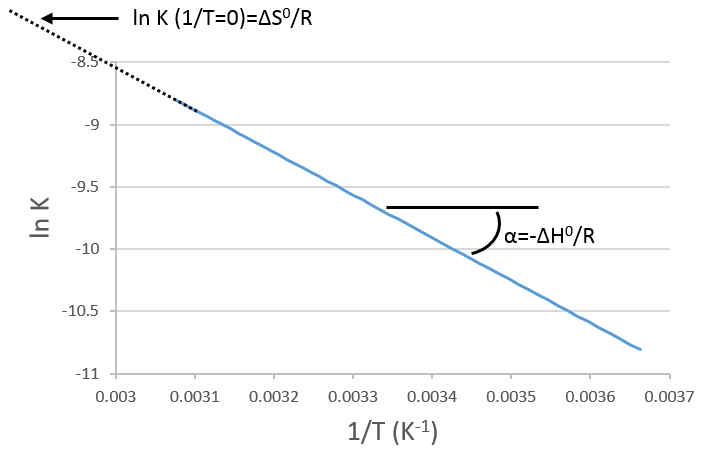
If we plot ln K in function of 1/T, we find a straight line the slope of which is –ΔH0/R.
The intersection with the axis at 1/T=0 will give us ΔS0/R. On the figure, the axis is not at 1/T=0 and the intersection of the curve with the axis doesn’t mean anything.
In the living, ΔG is usually very close to zero so that a stimulus can allow a reaction to take place. In our body, several reactions that would normally not work are coupled with the phosphorous removal of an ATP to allow the process to take place. The ATP is a reserve of energy of our body.
Chapter 7 : Electrophile additions on alkenes and alkynes
The interest of electrophile additions on C=C liaisons is to transform two sp2 carbons into two sp3 carbons and to add a chain or a group on the existing molecule.
As two carbons are involved in the reaction, the addition of the new group can give several products, with more or less (stereo)selectivity. Moreover, the transformation into sp3 carbons also introduces a regioselectivity that often has to be considered.
Consequently, we will discuss in this section the methods and the rules that have to be followed to obtain the desired product during the addition of an electrophile group on double or triple liaisons.
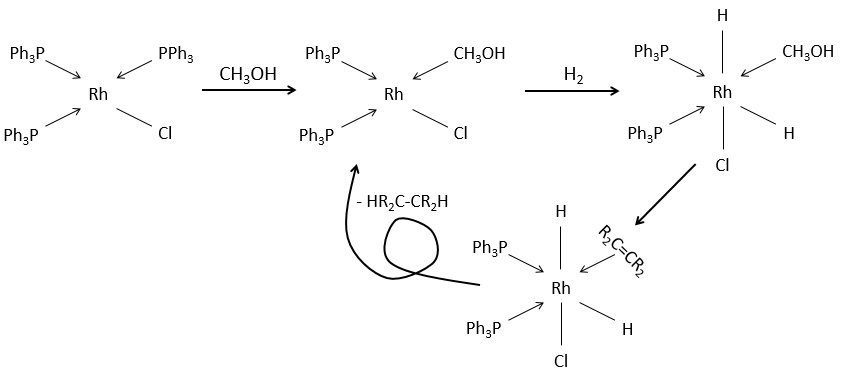
Catalytic hydrogenation
It is, in the principle, the easiest addition on a C=C liaison because there is no new group on the product. The sp2 carbons are reduced into sp3 carbons. Yet, this reaction is not spontaneous despite the fact that it is an exothermic reaction. The activation energy to break the H-H liaison is huge and a catalyst is required to perform the reaction.
As catalyst, we can use platinum (Pt), Raney’s Nickel (Ni) and Palladium on C (Pd/C).
The have the ability to dissociate the hydrogen atoms and to fix them on their surface, making them available for the addition on the alkene. As detailed in the kinetics section, the catalyst decreases the energy of activation of the reaction and the process can be depicted in 4 steps:
– approach and binding of the reactants
– displacement on the surface
– reaction(s)
– departure of the products
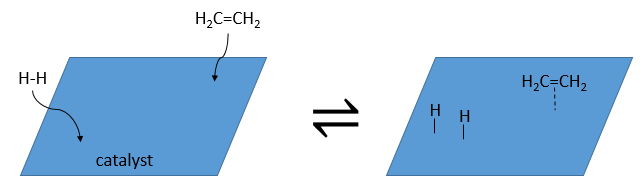
At the first step, the reactants take place on the surface of the heterogeneous catalyst. The amount of reactant that can take place on the catalyst depends on its surface. It is thus advised to use small particles of catalyst to increase the ratio surface/volume (or surface/mass). The alkene places itself parallel to the surface, in the direction of the π liaison.
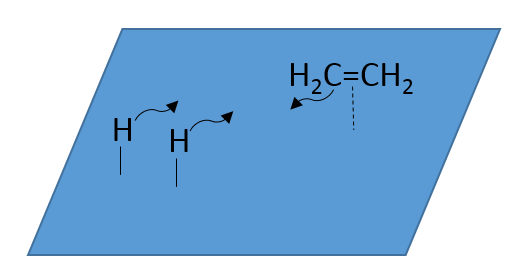
There is no reason that the reactants immediately bind on nearby spots. The second step is thus that the reactants are moving on the surface. They will eventually be in contact with each other so that the reaction can take place.
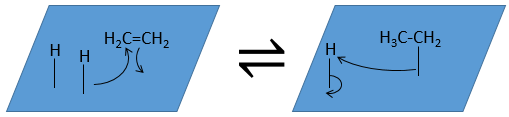
The third step (and eventually the next ones) is the reaction between the reactants. One activated hydrogen attacks one sp2 carbon while the π liaison is now connecting the second carbon with the platinum. The next step of the reaction is that the liaison between the carbon and the platinum attacks the remaining hydrogen.
As last step, the alkane leaves the surface of the catalyst, letting space for reactants to bind.
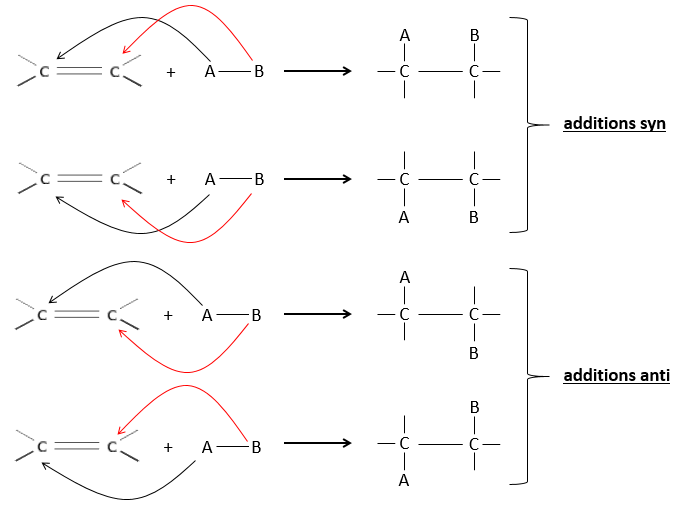
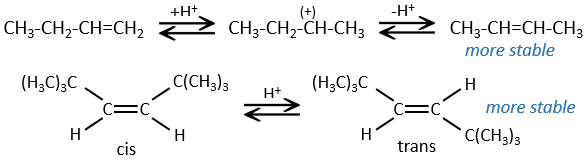
The hydrogenation is stereoselective, i.e. the place of the groups on the carbons are not equivalent: at the level of the C=C liaison, the molecule is planar. If the hydrogen atoms are fixed on the same side (but not on the same carbon) of the molecule. It is a syn addition. As the added groups are hydrogen’s, the product is thus cis (see nucleophilic substitutions about cis and trans products).
If the groups were added on the opposite sides of the molecules (still not on the same carbon), the addition would be anti and the product would be trans. This product is not observed because the reactants are bound to the catalyst and cannot move freely during the reaction. Both hydrogen’s are thus on the same side of the molecule before the reaction and after the reaction.
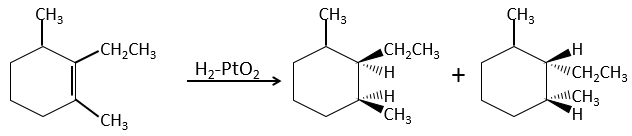
This is of importance only if, after the reaction, the newly sp3 carbon cannot rotate. It will be the case when the liaison is involved in a cycle or if there are voluminous groups. Moreover, the fact that we obtain only the cis product does not mean that only one product is possible. The reason is that there is one plane at each side of the π liaison (for a total of 2). If the two planes are equivalent, we will obtain a 50-50 racemic mix of two cis products.
If the planes are not equivalent, one product is favoured: the hydrogen’s are fixed on the least occupied side because the alkene places itself on the catalyst so that the voluminous groups are far from the catalyst.
Soluble catalysts can also be used for this reaction. It is the case for the Wilkinson’s catalyst chloro(tris(triphenylphosphine)rhodium(I).
It also lead to the cis products.
In terms of reactivity, the substituted carbons react slower than carbons with less groups because of the steric hindrance: the hydrogen’s are not very mobile on the surface of the catalyst and the π liaison has to be nearby to obtain the hydrogenation.
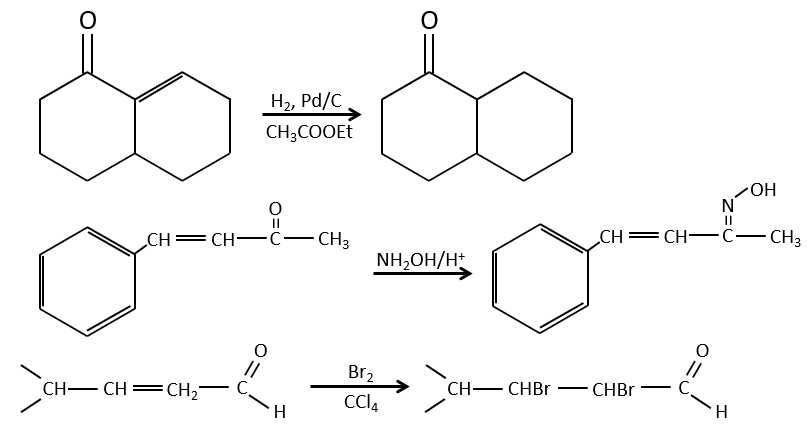
The alkynes also react faster than alkenes, allowing us to hydrogenate all the alkynes into alkenes before the formation of alkanes. We can thus limit the hydrogenation to the alkenes if we use a bad catalyst and put one equivalent of H2 by alkyne. We will obtain the alkane with 2 equivalents of H2 by alkyne.
Again, it will lead to the cis alkene. To obtain the trans alkene, we use sodium in ammoniac. The sodium generates a radical on one carbon and a negative charge on the other one.
The trans product is favoured for steric reasons.
Aromatic products can difficultly be hydrogenated with H2/cat (at 150°C) but it can also be reduced differently by the reduction of Birch, involving Na, NH3 and an alcohol.
Other electrophile additions
Addition of HX
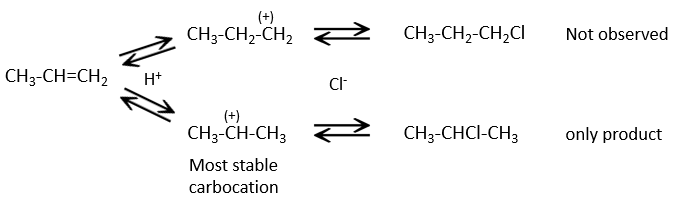
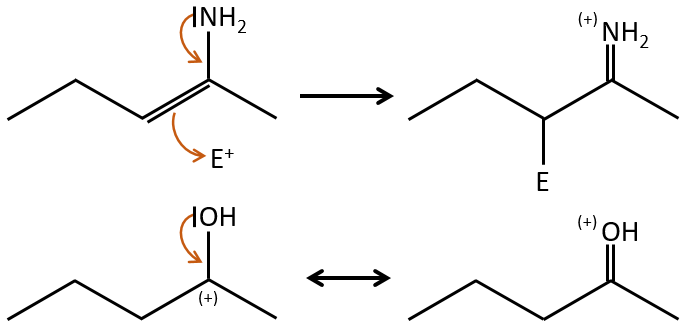
The other reactants HX containing a hydrogen atom can more easily be broken (or are already ionic) and do not require a catalyst. In the case of a halogen acid, because of their nucleophilic character, the π liaisons which are weaker than σ liaisons tend to attack electrophile molecules. In this case, the electrophile target is the proton. It is called an electrophile attack. The nucleophile X– attacks the positive carbon (or carbocation) afterwards.
This reaction does not involve stereoselectivity because there are two distinct steps but involves regioselectivity: it is the rule of Markovnikov that says that the halogen is fixed on the most substituted carbon, or inversely that the proton is fixed on the least substituted carbon. Personally, I prefer to remember that the most stable carbocation is formed. Remember that carbocations can rearrange the molecule to form the most stable carbocation.
Addition of water
Water is added to alkenes in presence of sulphuric acid.
The sulphuric acid is chosen because the sulphate is less nucleophilic than the water because the charge is stabilised by resonance. HCl has to be avoided because Cl– is more nucleophilic than H2O. Moreover, all the steps are reversible. It means that the newly generated alcohol can be dehydrated in the case of an excess of acid.
The presence of a carbocation explains some rearrangements of alkenes that can be observed in acidic solvents.
Addition of X2
Halogen’s are added to C=C to obtain trans products.
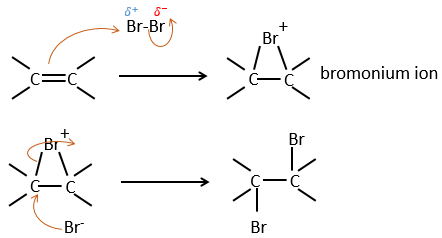
It is strange that something as charged in electrons as halogens are used as electrophiles for this reaction. The reason is that the liaison between the halogens is polarisable. A halogen will thus feel the electrons of the π liaison and transfer part of its electrons to the other one. The partially positive halogen can thus be attacked by the π liaison and forms an intermediate halonium that will be attacked by the negative halogen on the other side of the C-C liaison.
This reaction is stereoselective (always trans) and stereospecific (the result depends on the arrangement of the reactant). In presence of other nucleophiles, such as water, the reaction begins normally but there is a competition between X– and the nucleophile.
This reaction is slower on alkynes because the intermediate halonium is less stable. The halogenation is thus hard to control: the alkenes will react faster than the alkynes.
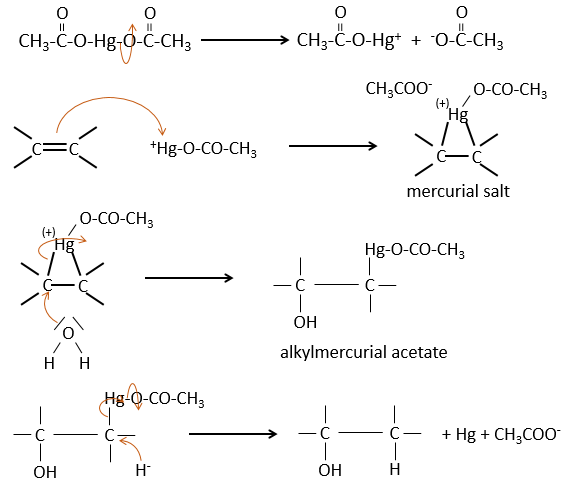
The oxymercuration reaction
This reaction is a useful way to form alcohols or ethers from alkenes. It involves mercurial acetate and water/alcohol in THF as solvent. The nucleophilic opening of the water/alcohol is done in anti and on the most substituted carbon (so there is more space for the mercurial acetate).
The oxymercuration follows the Markovnikov rule but there is no carbocation involved in the process. As all the additions, it is regioselective.
Water leads to the formation of an alcohol and we can use an alcohol instead of the water to obtain an ether.
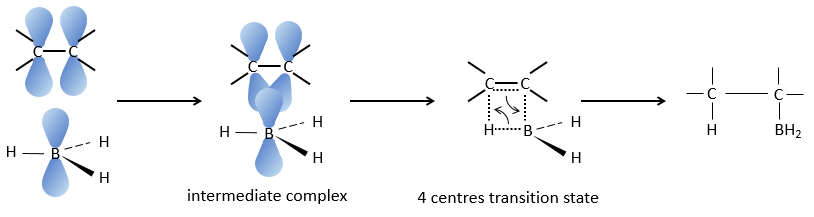
Hydroboration reaction
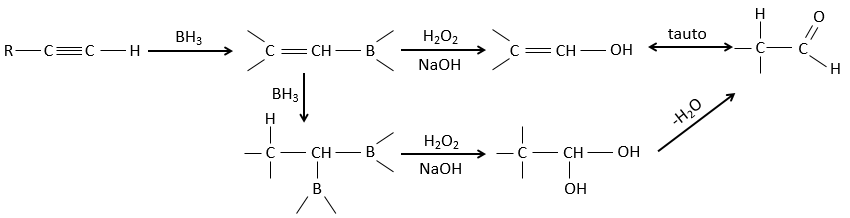
BH3 (borane) is a Lewis acid that is stable under the form of a dimer and can replace its 3 hydrogen by 3 carbon chains in THF (tetrahydrofuran (CH2)4O). Once the chains are bound, it is possible to remove the boron by an oxidation with H2O, NaOH and H2O2 to obtain as many alcohols.
This reaction does not follow the Markovnikov rule (anti-Markovnikov) and is stereoselective. The mechanism of reaction involves the empty p orbital of the boron that interacts with the π liaison to form a complex. This complex allows a transition state with 4 centres wherein the liaisons move.
The Markovnikov rule applies when the hydrogen is positively charged. In the present case, we add H– and BH2+.
The removal of the boron is made with retention of configuration and is stereospecific. The boron is less electronegative than the carbon and is thus giving its electrons. NaOH takes a proton from the H202 to form HOO– that attacks the boron, transferring its negative charge. There is a rearrangement occurring that puts an oxygen between the chain and the boron.
The water and OH– take action next to remove the boron.
This addition can also be done on alkynes to form aldehydes through tautomerization.
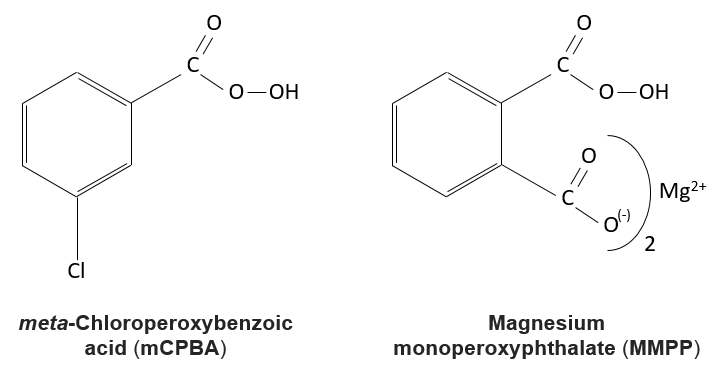
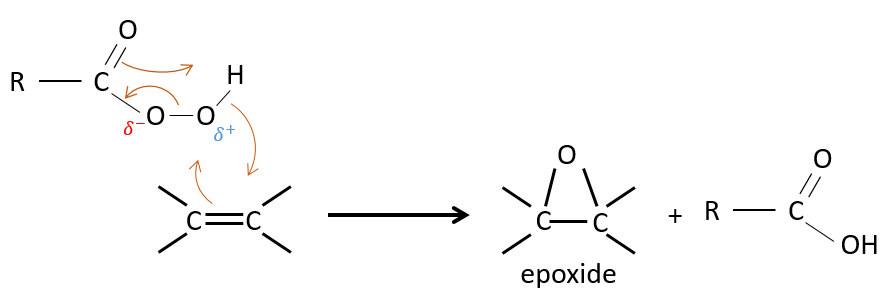
Reaction of alkenes with peroxycarboxylic acids
The peroxycarboxylic acids are generally unstable. The MCPBA and the MMPP are however stable peroxyacids vastly used in laboratory.
One of the oxygen of the peroxycarboxylic acids is electrophile. Those acids can thus react with alkenes to form epoxides and the carboxylic acid.
The addition is thus a concerted reaction, is stereospecific and is syn. The reaction is made on the less hindered plane of the alkene. The reactivity increases with the amount of substituents that share their electrons with the π liaison (alkyl chains for example).
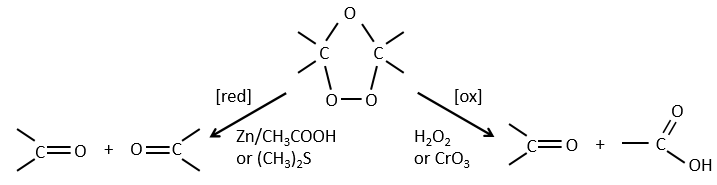
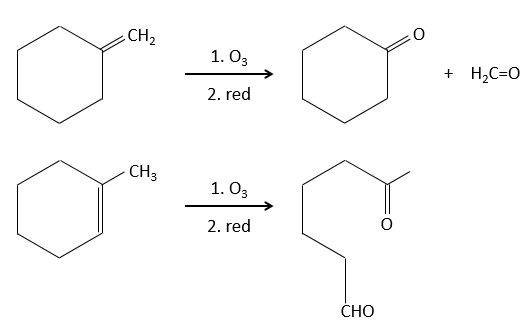
Ozonolyse
The ozone can break double liaisons. As a first step, it opens the double liaison to give the intermediate called molozonide.
It breaks to form ozonide that can next be oxidized or reduced.
The following table gives the products of the ozonolyse as a function of the substituents of the double liaison.
The ozonolyse is thus a good way to obtain ketones and carboxylic acids from alkenes. The method is also useful to determine to position of a double liaison in a molecule when we cannot easily determine it with usual techniques.
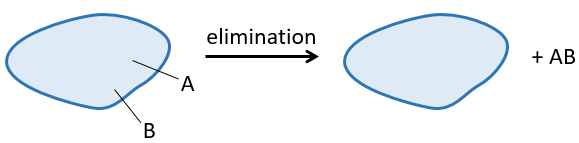
Chapter 8 : Reactions of elimination
A reaction of elimination is a reaction during which one molecule loses two fragments A and B as a neutral substrate AB.
The two fragments A and B that are removed can be removed from the same carbon, in which case we talk about a 1,1 elimination, from two adjacent carbons (1,2 elimination or beta elimination) or two carbons separated by one carbon (1,3 elimination). The 1,2 elimination is the most common one.
Elimination 1,1
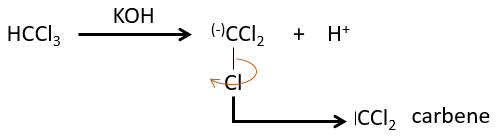
The two fragments are removed from one single carbon. It leads to the formation of a higly reactive carbene.
This reaction is possible because the chlorine atoms take the electrons from the carbon. Because of that, the C-H bond is destabilised and a strong base can remove the proton.
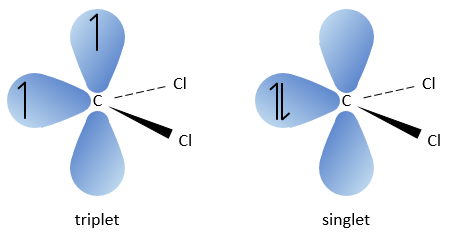
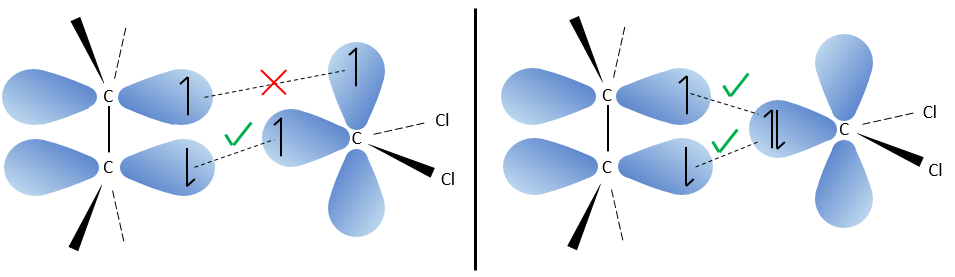
The carbon of the carbene is a singlet and is less stable than a triplet. It will thus react quickly with double liaisons to obtain a cyclopropane chain. A triplet would not be able to attack the π liaison.
The reaction is stereoselective (on the same side of the plane).
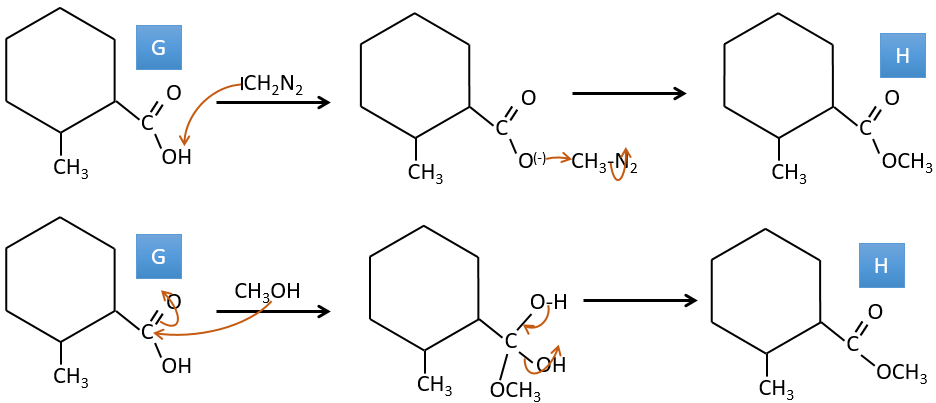
The smallest carbene is the methylene that can be produced from diazomethane (check nom anglais). The diazomethane is toxic and explosive so the reaction has to be controlled.
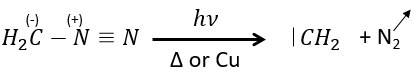
It can also be used to produce methyl esters.
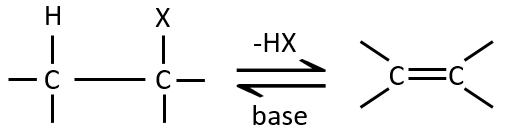
Elimination 1,2
This kind of elimination leads to the formation of new π liaisons. It is the opposite of a reaction of addition. We will only discuss the main reaction of β elimination but there can be other mechanisms involved to obtain such a reaction.
Similarly to the substitutions, where there is a mechanism with a kinetic of order 1 (SN1) and one of order 2 (SN2), there is an elimination of order 1 (E1) and of order 2 (E2).
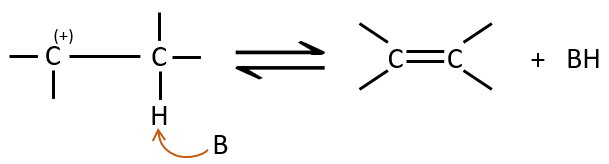
E1 mechanism
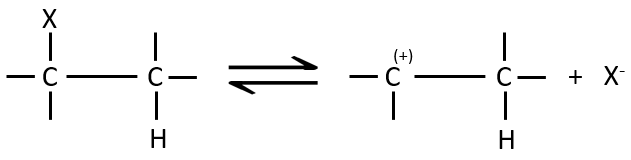
The first step of the reaction is the departure of one anion and the formation of a carbocation. This step is slow and is determining the speed of the reaction.
The second step is the capture of a proton on the adjacent carbon by a base. It leads to the formation of the π liaison to have a neutral species.
We can know if an elimination is of order 1 from
- the order of the kinetic of reaction (order 1).
- the isotopic effect: if the hydrogen is replaced by a deuterium, we don’t see any modification of the speed of reaction. It is so because the hydrogen doesn’t take part in the determining step. If it was involved, the speed would be divided by 5 to 8.
- the stability of the carbocation: the stability of the carbocation (degree of substitution or hyperconjugaison) affects the speed of reaction.
- rearrangements: explained by the existence of a carbocation.
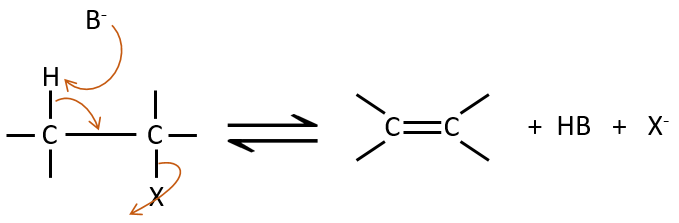
E2 mechanism
The kinetics is of order 2 and involves a reaction in one step, where the base takes the proton and the departure of the leaving group are simultaneous.
This reaction is only made if the proton and the leaving group are in anti positions.
The argument in favour of the E2 mechanism are
- a kinetic of order 2
- a huge isotopic effect
- no rearranging
- huge influence of the energy of the C-X bond (X– is the leaving group)
Competition between the mechanisms
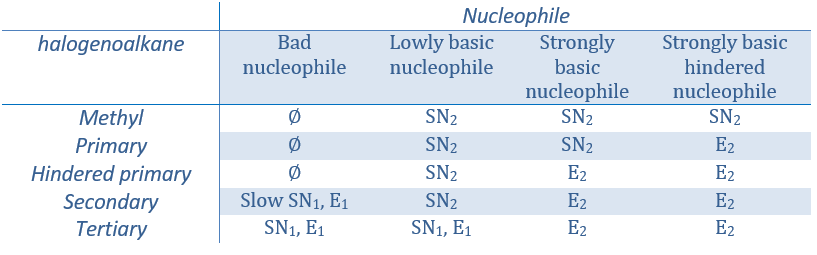
As for the nucleophilic substitutions, there is a competition between the two mechanisms. It is not always 100% of E1 but it can be a mix of both, eventually leading to a racemic melange of products. The strength of the base and the steric hindrance influence which elimination mechanism is used: a strong base favours the E2 mechanism while a weak base and steric hindrance favours the E1 mechanism.
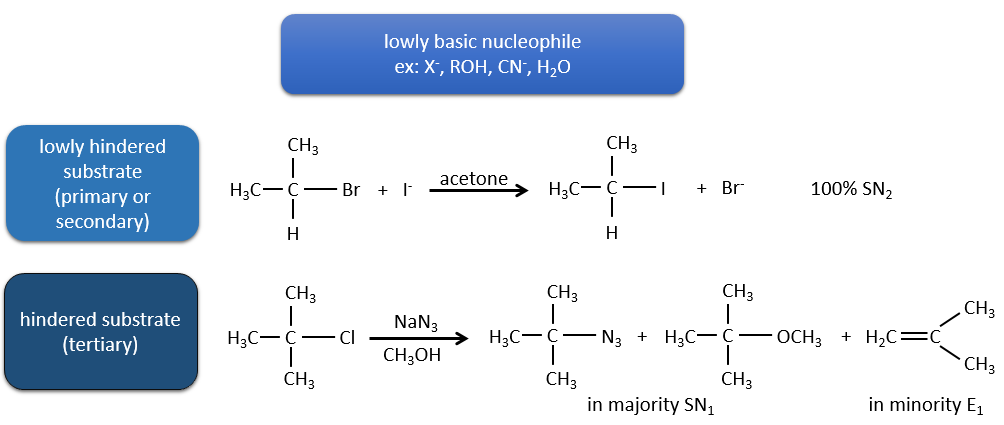
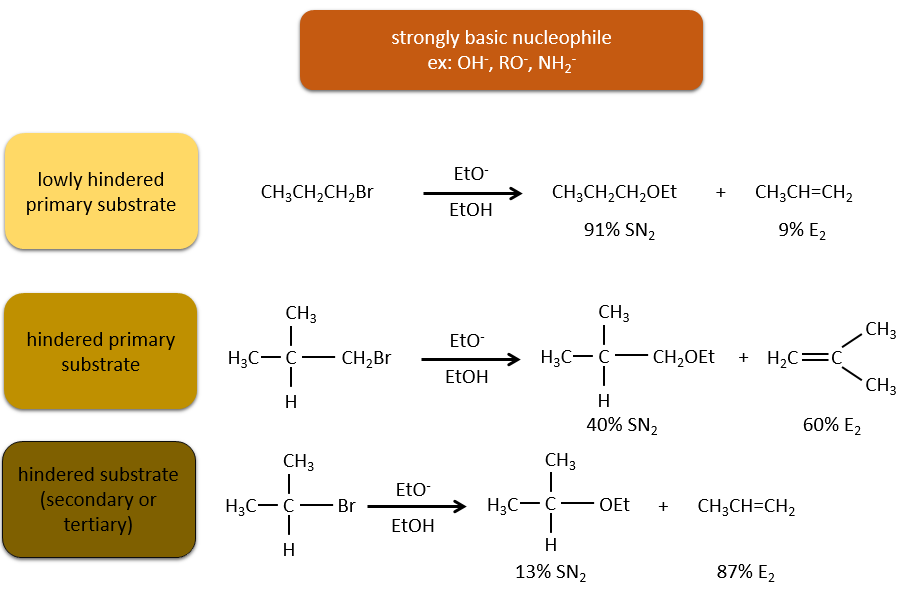
Now, the molecules with a good leaving group can often also be the target of a substitution reaction in presence of nucleophiles. There is thus a competition between E1, E2, SN1, SN2 and eventually other reactions. The three main parameters to consider to determine which reactions should occur are the strength of the base, its nucleophilicity and the steric hindrance.
Nucleophiles that are bad nucleophiles have good yields with SN2 with primary and secondary substrates. If the steric hindrance is larger, the main product becomes the SN1 product. If the nucleophile is a strong base, the main product is the SN2 but if the steric hindrance increases, the elimination becomes more important.
Nucleophiles that are strong bases and that are hindered favour the elimination.
To resume:
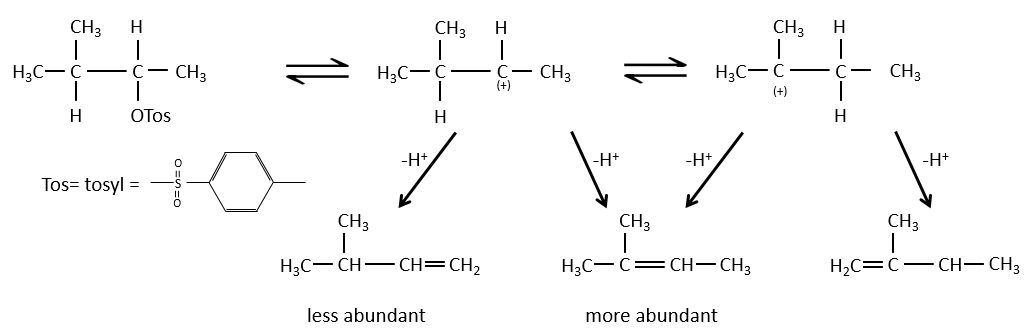
Regiochemistry of the elimination
When the carbon wearing the leaving group is not at one extremity of a chain, there can be several possible products. We can predict which hydrogen will be removed.
- If the generated double liaison can be conjugated with other π liaisons, those products will be favoured.
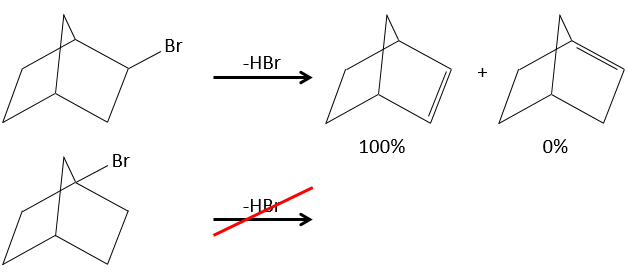
- In the case of bridged substrates, the product never involves a π liaison on a bridgehead carbon.
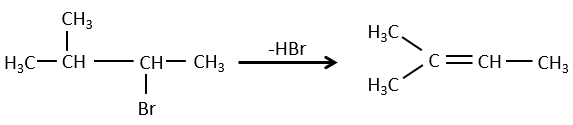
- For E1 eliminations: the elimination is determined by the stability of the formed olefins. The most substituted C=C is thus favoured. It is the rule of Zaitsev.
– There can be exceptions because of steric hindrance
- for E2 eliminations, one H in anti is required
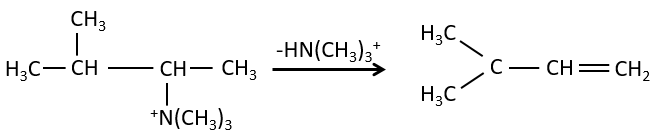
- the rule of Zaitsev is followed if the leaving group is not charged (most substituted C=C)
- it is the opposite it the leaving group is charged: it is the rule of Hofmann
Configuration of the product
In the case of one E2 elimination, the reaction is stereospecific and there is thus only one possible configuration.
In the case of one E1 elimination, the product is more stable if the voluminous substituents are in trans.
Dehydratation of alcohols
This elimination does not occur in basic or neutral environments: OH– is a bad leaving group and we would form –O– in presence of a strong base.
In an acidic environment, the elimination can be done by E1 or by E2. The E1 is favoured in the case of substituted products and the E2 is the main mechanism for primary carbons.
Reactivity: tertiary>secondary> primary
E1 E1 E2
Fragmentation of 1,3 diols
It is one case of 1,3 elimination during which the molecule is cleaved
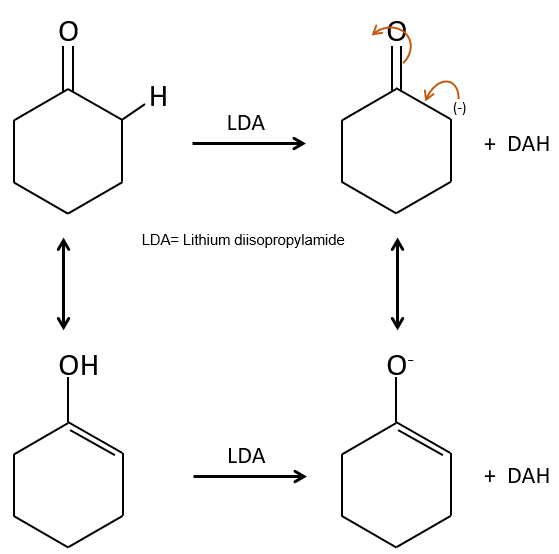
Chapter 9 : carbanions in α of carbonyl
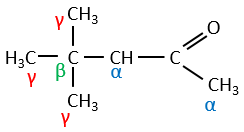
In the previous section, we discussed the possible reaction on the carbonyl group of organic molecules. The carbon is an electrophile and the oxygen is a nucleophile. Yet, the presence of a carbonyl can imply other processes. The hydrogen’s that are on a carbon neighbour of a carbonyl group, i.e. the carbon in α of carbonyl, are acid and strong bases can snatch it.
Its pKa is around 20 (for comparison, the hydrogen of a –C-H has a pKa of 40, a =C-H a pKa of 37 and –O-H a pKa of 18). The result is the enolate ion. It is stabilised by resonance with the carbonyl.
Tautomerization
The enolate ion can react by its oxygen or the carbon in α.
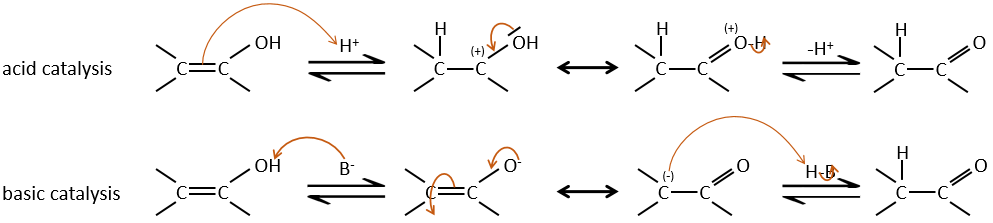
Enols are usually unstable and tautomerize into the corresponding carbonyl. It is the enol-ketone tautomerism. The tautomerization is done by acidic or basic catalyse.
The difference of energy is about ΔG=15kcal in favour or the ketone form. The enol-ketone equilibrium can be displaced if one form is stabilised by the structure of the molecule.
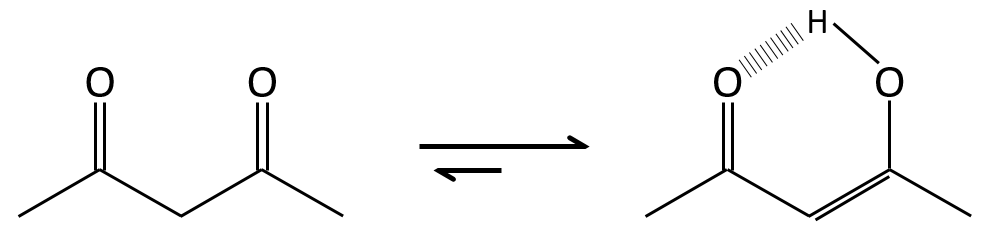
The tautomerization allows to modify the conformation of the molecule. A cis molecule tautomerizes to become trans and decrease the steric hindrance.
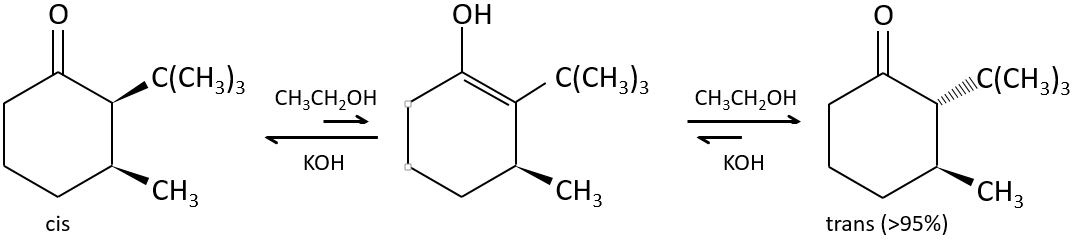
We can also exchange hydrogen’s for its isotopes because of the tautomerism.
The chemical properties of isotopes are almost identical (because given by the electrons), but some physical properties can be different between isotopes of the same element. The speed of reaction and the ebullition temperature are two examples of properties that change depending of the isotope. It is thus possible to separate the species wearing isotopes by distillation or by centrifugation.
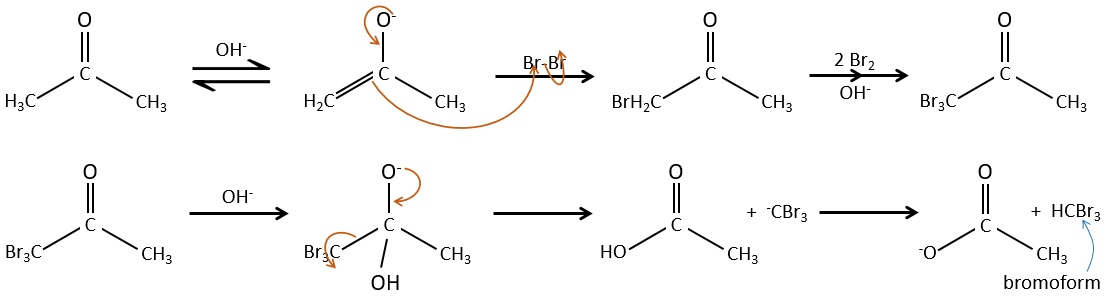
Halogenation
The hydrogen can also be exchanged with halogens through acidic or basic catalyse. In this case, the results are different depending on which catalyst we use.
– Acid catalysis:
Once one halogen is on the molecule, it is harder to form the enol because it is more difficult for C=O to catch a proton due to the inductive captor effect of the halogen.
– Basic catalysis:
During the basic catalyse, we don’t have to protonate the carbonyl and the halogenation can take place as many times as there are α protons.
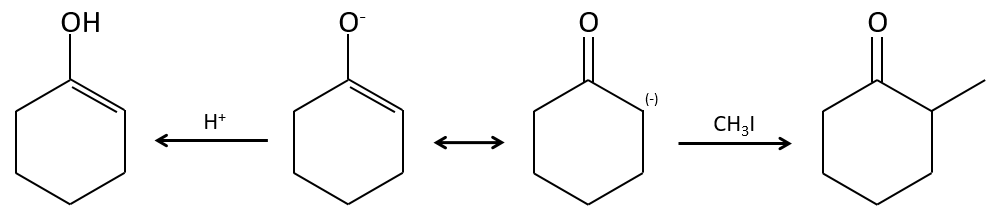
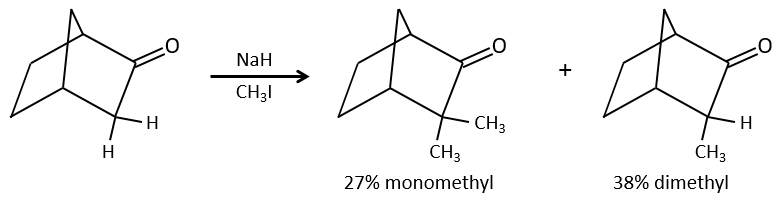
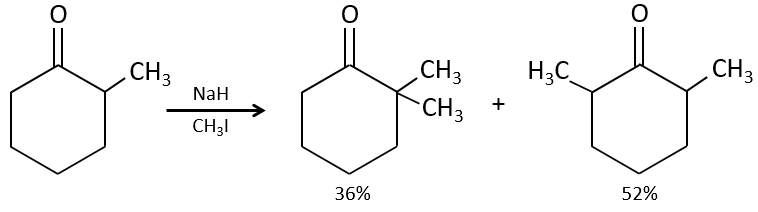
Alkylation
We have seen in the previous section that NaH alone doesn’t reduce carbonyls. However it has an effect on the carbon in α of carbonyls. It is a good way to introduce an alkyl group at this position.
A strong base can also take the proton α of carbonyl.
One problem is that the reaction can continue if there are several hydrogen’s in α of carbonyl and polyalkylation is frequent, leading to a racemic mix of products.
Moreover, the regioselectivity is low, giving an additional possibility of product.
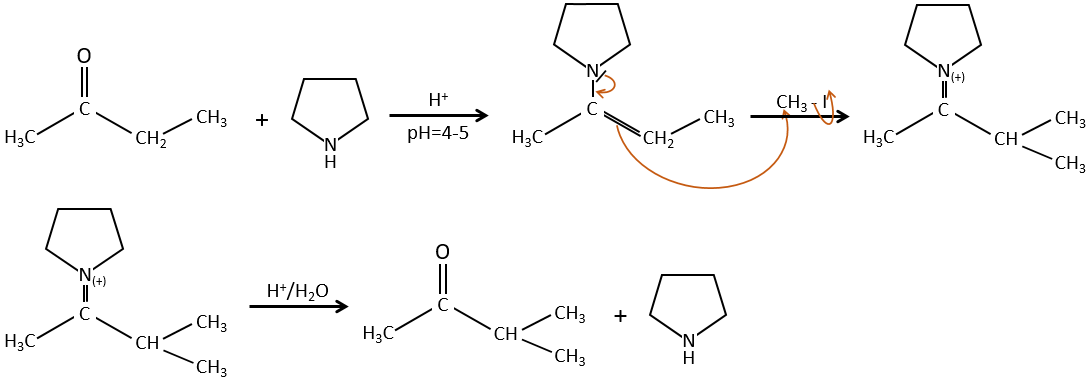
To avoid polyalkylation, we can replace the oxygen by pyrrolidine (C4H9N) to obtain the corresponding enamine that has the advantage of a low polyalkylation.
This protection is also effective for aldehydes that are subject to the aldol condensation reaction in basic environments.
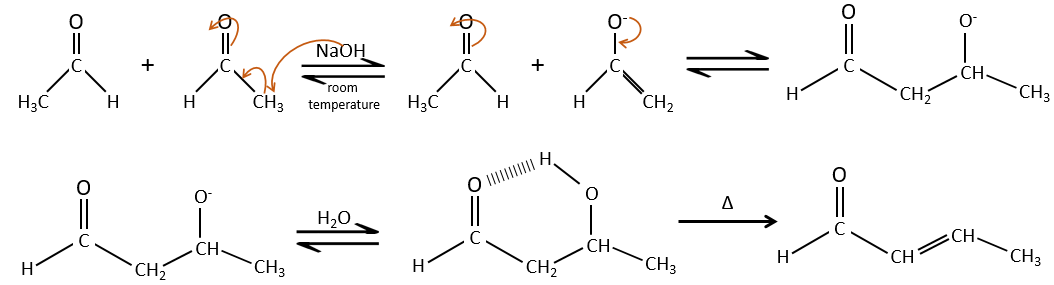
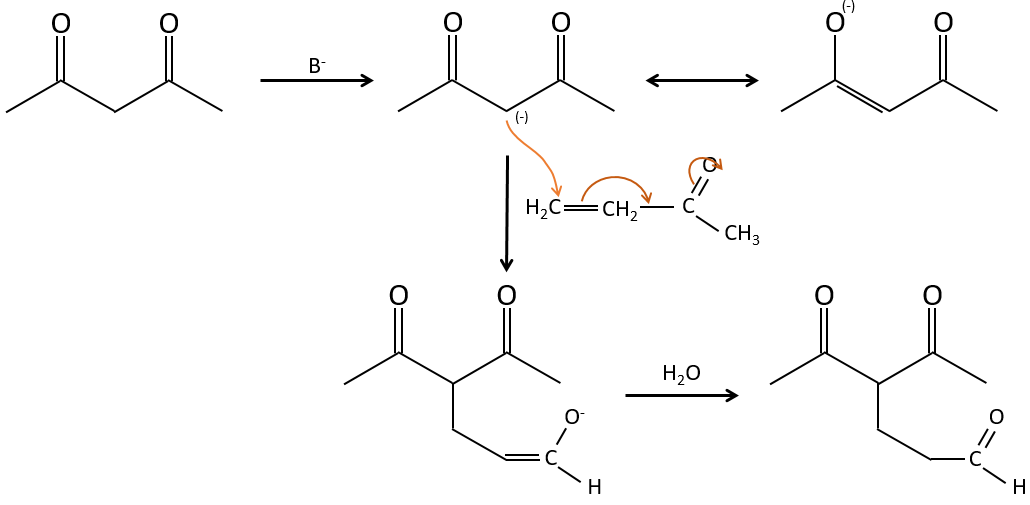
Aldol condensation
If we add a few NaOH in a solution of acetaldehyde, dimers are formed. The first step is the deprotonation in α of carbonyl by the base to obtain the enolate ion that attacks next another aldehyde, leading to the formation of a β-hydroxyaldehyde. The β-hydroxyaldehyde is stabilised by its internal hydrogen bond.
If we heat up the solution, the molecule loses a water molecule to form an enone (double liaison conjugated with a carbonyl).
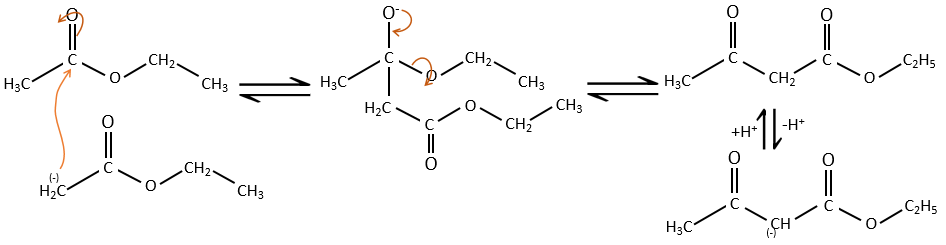
Condensation of Claisen
The analogue reaction for esters is called the condensation of Claisen. NaOH is not used in the present case because it would cleave the ester. We can use sodium ethoxide instead for instance to obtain the enolate ion.
As for the aldol condensation, the enolate ion attacks another ester to obtain β-ketoesters.
The condensation of Claisen can be made with two different esters (mixt condensation of Claisen) or between two esters in the same molecule (intramolecular condensation of Claisen).
The intramolecular reaction is favoured in comparison to the intermolecular one because it does not decrease the entropy.
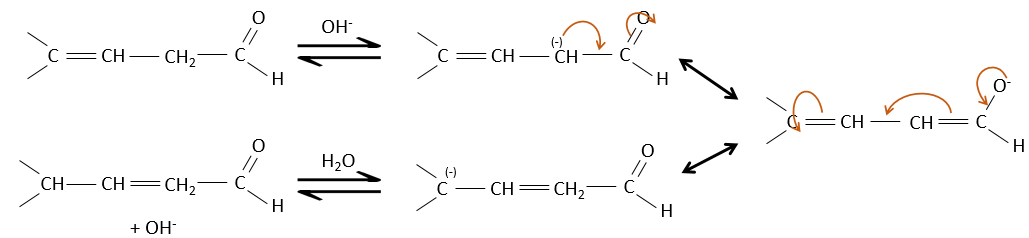
Properties of α,β unsaturated aldehydes and ketones
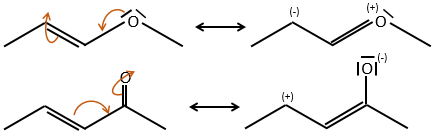
Such species are stabilised by resonance.
They are way more stable than β,γ-unsaturated aldehydes/ketones that rearrange themselves into the α,β unsaturated compound in presence of a base.
Obviously, the double liaison and the carbonyl groups can go through reactions independently, such as addition reactions for example.
But additions can also be made in several cases on the conjugated system. Those are 1,4 additions.
The nucleophilic attack is possible on the carbon of the double liaison because it is depleted by the conjugation with the carbonyl.
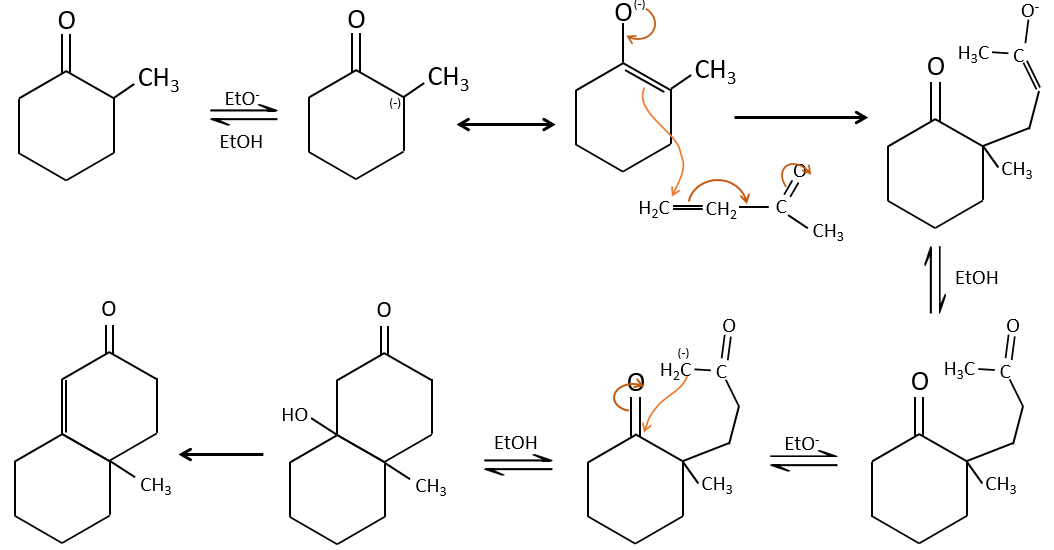
The Michael’s addition is the 1,4 addition of an enolate ion on an enone:
A Michael’s addition can be followed by an intramolecular aldol condensation, the reaction is known as the annulation of Robinson.
Chapter 10 : Reactions of carboxylic acids and their derivatives
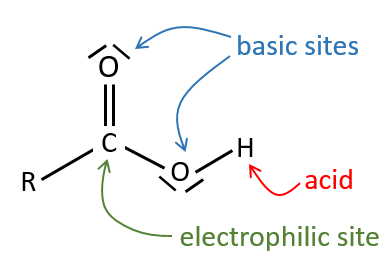
All the atoms of carboxylic acids groups have a specific character. The group is thus ambident: it possesses two or more alternative and strongly interacting distinguishable reactive centres. It has acidic and basic properties.
A carboxylic acid is more acid than the corresponding alcohol because the conjugated base, the carboxylate, is stabilised by resonance (pKa≈5 vs pKa≈17).
The oxygen of the carbonyl is more basic than the other one because the positive charge is more stabilised.
Synthesis of carboxylic acids
There are several ways to form carboxylic acids:
- by oxidation:
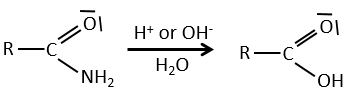
Carboxylic acids can be made by the oxidation of aldehydes or of alcohols. We can use CrO3 or KMnO4 as oxidants for instance.
- by Grignard

A reactant of Grignard can react with CO2 and then with water to form a carboxylic acid
- from nitriles

In acid environments, nitriles react with water to generate new acids and free a molecule of ammoniac.

This method can be used to extend a carbonic chain. Once a carboxylic acid is obtained, we reduce it to obtain an alcohol. The –OH group is removed by nucleophilic substitution and the whole loop restarts. Each loop adds one carbon to the chain.
The derivatives of carboxylic acids are
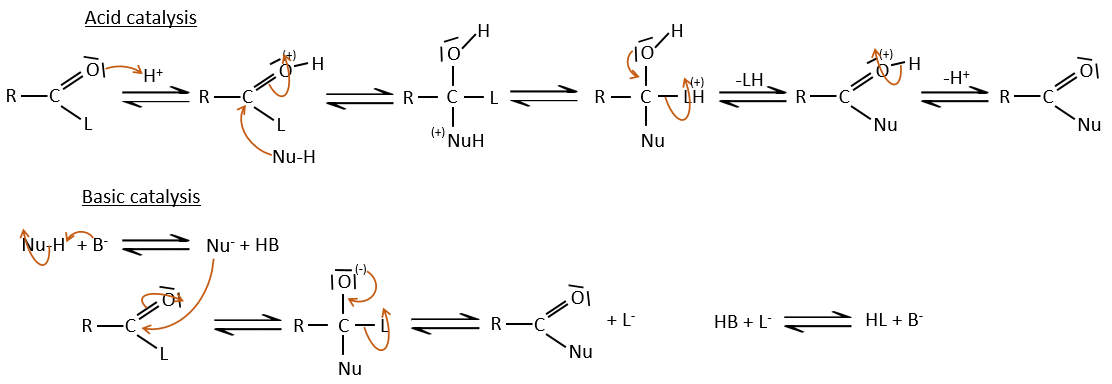
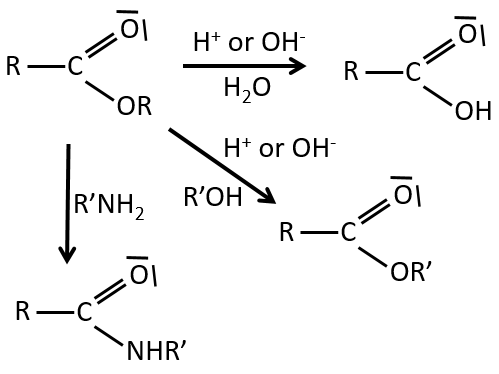
Reaction of Addition-Elimination
Carboxylic acids and their derivatives are attacked by nucleophiles on the carbon, as it is done for ketones and aldehydes. However, this addition is followed by an elimination.
It is thus the substitution of one group by the nucleophile at the condition that the group L that was previously on the carbonyl is a better leaving group than the nucleophile.
Cl–>RCOO–>RO–>OH–>NR2–>C–
As for ketones and aldehydes, the reaction can be catalysed by an acid or a base.
Note that the addition-elimination reaction for carboxylic acids is in competition with acid-base reactions. OH– is not a very good leaving group and if the nucleophile is a strong base, the carboxylate is formed. In the case of a nucleophile which is not a good base, there is a competition between the AE and the AB reactions.
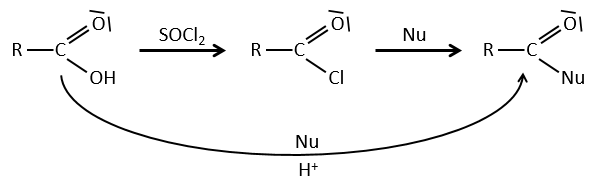
Formation of the acyl chloride
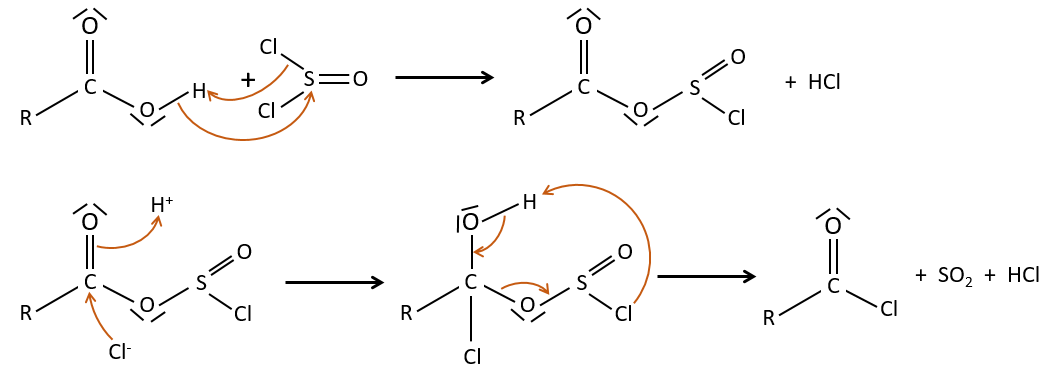
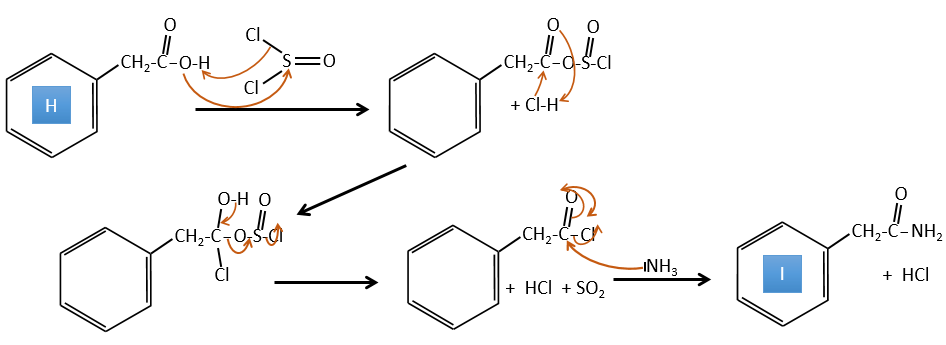
From what we wrote just above, we cannot replace RCOOH by RCOCl because Cl– is a better leaving group than OH–. However, there is a trick to make this reaction possible: we use thionyl chloride (SOCl2). The oxygen bound to the hydrogen in COOH is a nucleophile and can attack the sulphur atom, expelling a chlorine that catches the proton on its way. The newly formed chlorydric acid can now react with the thioester, eliminating a molecule of SO2 and of HCl.
The same kind of mechanism is used to produce acid bromine from carboxylic acids and PBr3 (phosphorous tribromide). Yet, those reactions don’t work with HCOOH because the products HCOCl and HCOBr are unstable. They decompose in carbon monoxide and the corresponding acid.
Formation of esters
Carboxylic acids react with alcohols to produce esters.
Strong acids catalyse this reaction.
RO– is a slightly better leaving group than OH– so we want to displace the equilibrium towards the right by the use of an excess of alcohol or carboxylic acid and by the removal of water from the system. If we want to do the hydrolysis of an ester, i.e. the reverse reaction, we use an excess of water. It was shown that the hydrolysis of esters works this way (attack of the water on the carbonyl and not an attack of the water on R’) by the use of isotopes for the esteric oxygen.
Another way to obtain esters is the use of diazomethane, reaction that we have seen at the beginning of the elimination chapter.
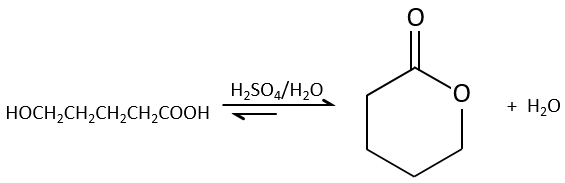
Intramolecular esterifications are more favourable than intermolecular ones for entropic reasons and are especially favourable if a cycle of 5 or 6 atoms is formed.
This kind of cycle is called a lactone (δ-lactone if a cycle of 6 atoms, γ-lactone if a cycle of 5, etc.). Lactones are sensible to the hydrolysis.
Formation of amides
Under normal conditions, an amine reacts with a carboxylic acid to form a salt (ammonium carboxylate) through an acid-base reaction. Once the amine has taken the proton, it cannot attack the carbonyl anymore.
If we heat up the system, the reaction goes back and another process, thermodynamically more favourable occurs, leading to the formation of an amide. In an amide, the nitrogen is not basic.
Intramolecular reactions are possible and lead to the formation of lactams.
Reactions of carboxylic acids and their derivatives
We have shown several reactions of the carboxylic acids. It is often interesting to consider to transform the carboxylic acid into an acyl chloride prior to the desired reaction. Acyl chloride are usually more reactive and this additional step in the process can increase the global yield of the reaction.
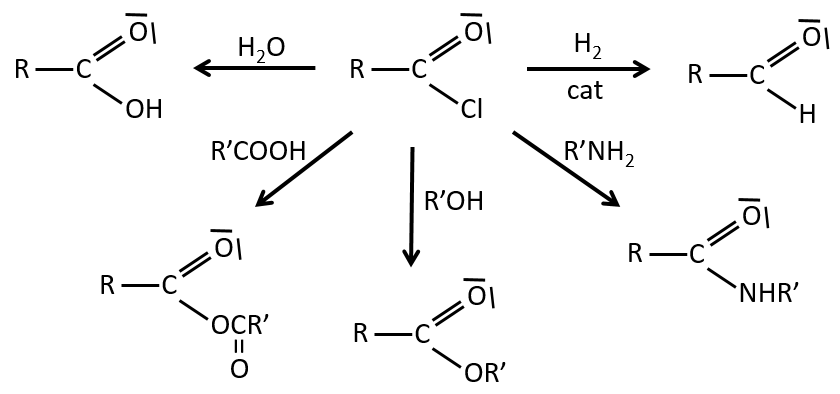
Reactions of acyl chlorides
From the acyl chloride, we can obtain many other functional groups.
Reactions of esters
As ester are less reactive than the acyl chlorides, less reactions are available. We can hydrolyse the ester, exchange the esteric chain with another one or generate an amide.
An additional reaction is to use a Grignard reactant on an ester to obtain a tertiary alcohol. The ketone is more reactive than the ester so the reaction continues.
Reactions of amides
Peptide bonds can be hydrolysed.
Reactions of nitriles
The carbon atom from a nitrile is at the same oxidation state than the one of the carboxylic acid. A nitrile in presence of water and acid leads to the formation of a carboxylic acid and the rejection of ammoniac.
Nitriles can also react with reactants of Grignard but the reaction stops at the formation of ketones.
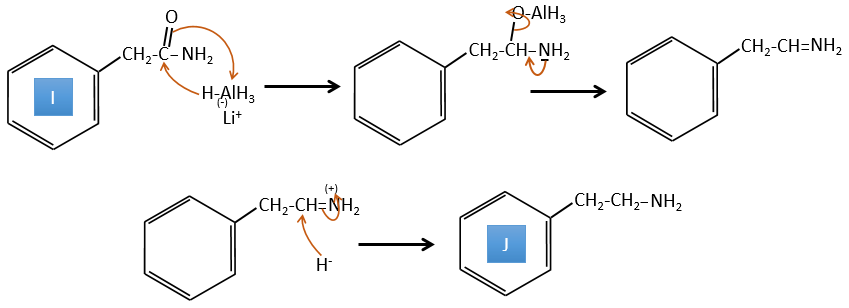
Nitriles can also be reduced into primary amines by LiAlH4.
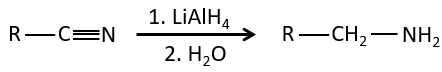
Chapter 11 : Reactions of substitution on aromatic cycles
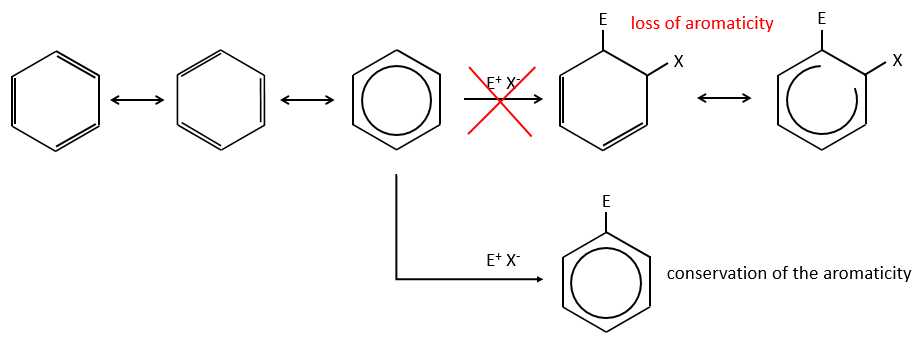
Aromatic cycles, such as the benzene, are very stable because of their energy of resonance. As a result, it is very difficult to “open” the cycle by an usual reaction of addition.
Instead of addition reactions, we observe reactions of substitution. The mechanism involves two steps.
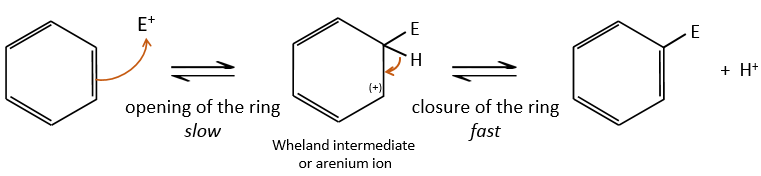
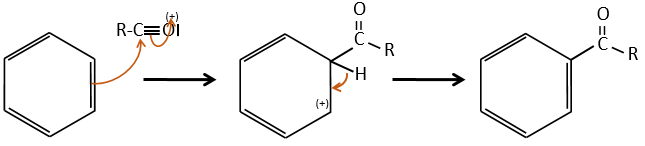
- the first step is the electrophile attack of one pi liaison on an electrophile. As this step implies the loss of aromaticity of the substrate, this step is slow and is the determining step of the reaction. The product of this step is called an intermediate of Wheland or an arenium ion.
- the second step involves the removal of a proton from the cycle to regenerate the aromaticity. This step is fast.
Most of the electrophiles have to be activated to allow the first step of the reaction. It is done by a Lewis acid.
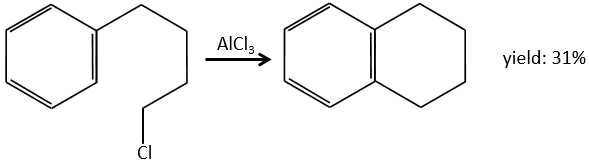
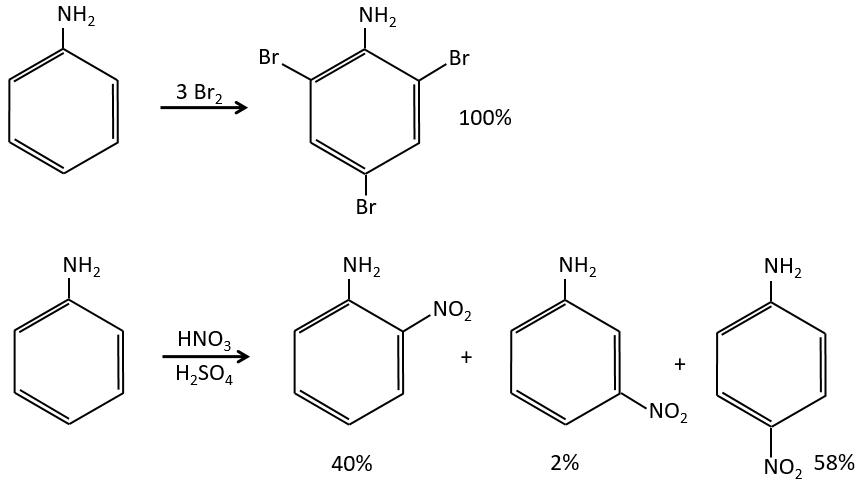
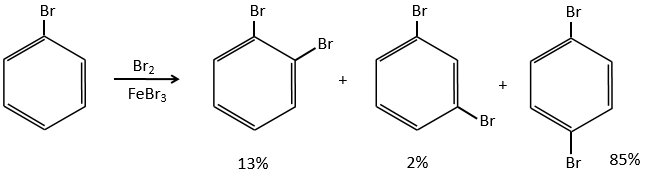
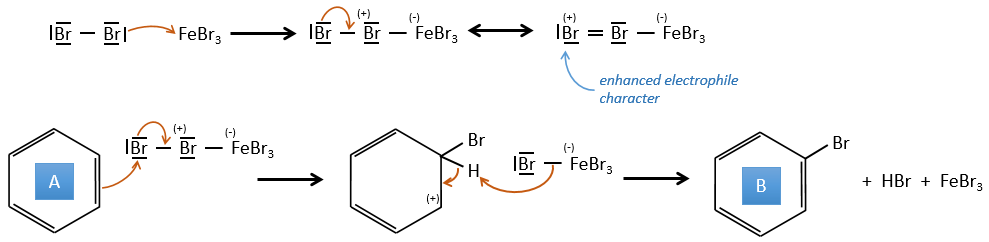
Halogenation
FeBr3 and AlCl3 can be used as Lewis acids to bind a halogen (Br and Cl respectively) on a benzene ring.
They enhance the electrophile character of the halogen that can now be attacked by the aromatic substrate.
FeBr4– acts like a base to take a proton and close the ring.
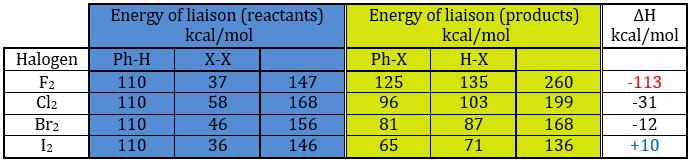
In the following table, we can find the energies of liaison involved in the process for the halogens. On the left, we have the energies for the reactants and in the middle column we have the energies for the products. The enthalpy of reaction is shown on the right column.
If we take a look at the variation of energy involved by a halogenation, we see that the enthalpy of reaction is positive for iodine. The reaction is thus not done. The reaction is highly exothermic for F2. In fact, this reaction is explosive. For Cl and Br, we need to use catalysts (the Lewis acids).
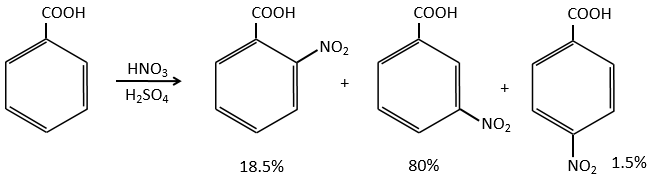
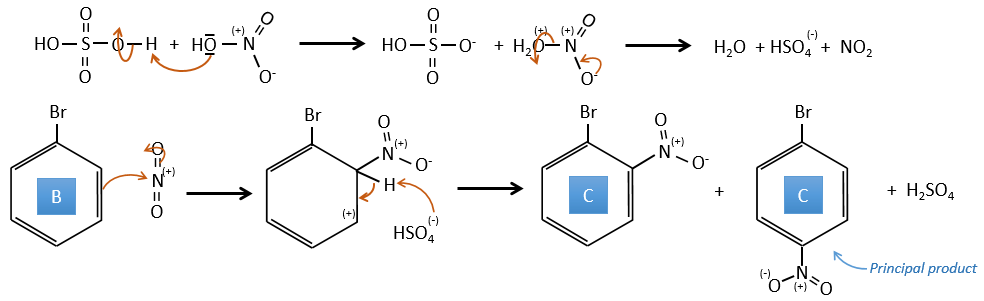
Sulfonation and nitration
SO3 and NO2+ are electrophile enough to bind with an aromatic ring.
The nitrate can be reduced selectively to obtain an amine.
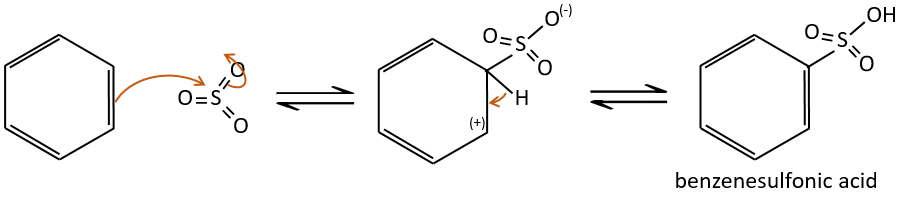
Sulfonation
The sulphur atom is electrophile because of the electrocaptor character of the oxygen’s. However, the reaction is reversible in presence of water to form sulphuric acid. This process is exothermic and we should keep an eye on it.
We produce detergents from the benzenesulfonic acid.
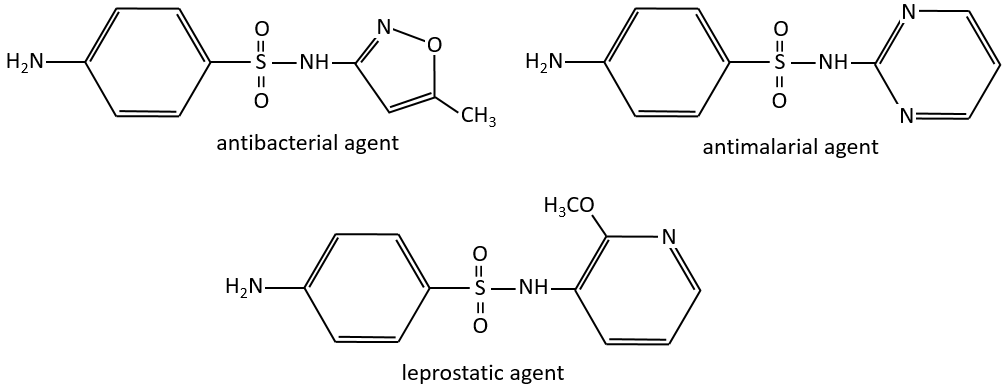
And from that point we can produce sulfonamides that are usually good antibiotics.
The first of this kind was the Prontosil (4-[(2,4-Diaminophenyl)azo]benzenesulfonamide) in 1932, developed by Domagk at Bayer, who won a Nobel prize in medicine for it in 1939. The research program was designed to find dyes that might act as antibacterial drugs in the body. The discovery and development of this first sulfonamide drug opened a new era in medicine. Other examples of antibacterial agents follow:
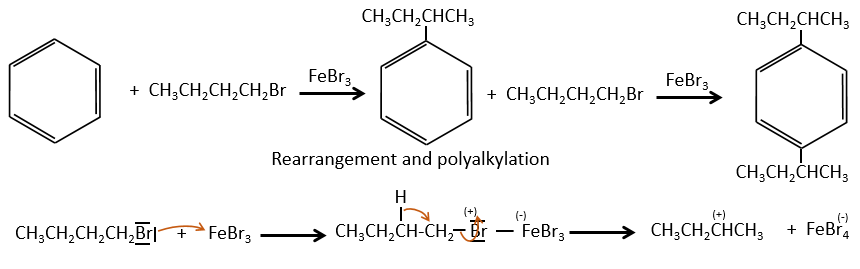
Alkylation of Friedel-Crafts
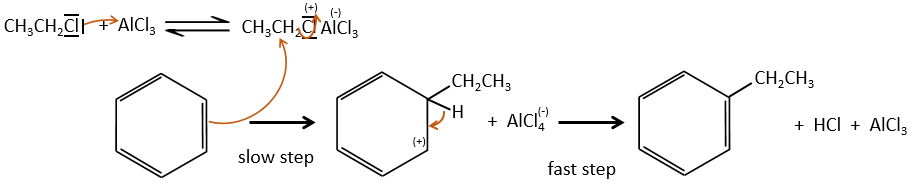
This reaction, as its name mentions, allows to bind a chain on an aromatic ring. The chain that is to be added has to have an electrophile carbon. Again, we need a Lewis acid to do this reaction. The first step is the activation of the halogenoalkane by the Lewis acid.
Next, the cycle attacks the alkane, ejecting the halogenated Lewis acid. The product of this step is called an intermediate of Wheland or an arenium ion. This step is the determining step of the reaction, involving the opening of the ring due to the electrophile attack. A proton is taken by the halogenated Lewis acid to give the aromaticity back with the recovering of the Lewis acid and the liberation of an acid. This step is fast with regard to the previous step. As a global result, we added a new carbon chain on the phenyl.
The halogen on the added chain is not mandatory. An alcohol can do the job as well, or other precursors of carbocations.
The alkylation can be intramolecular if it results in a new cycle.
Limitations of the method
The alkyl group that has been added to the phenyl is an inductive donor group. It means that it gives some of its charge to the phenyl, increasing its ability to attack electrophilic carbons. As a result, the alkylation process does not stop after the addition of one chain if there is still places on the phenyl to greet new ones (we will see a bit later on which spot which group can be added).
A second limitation is the rearrangement of the carbocation (as usual).
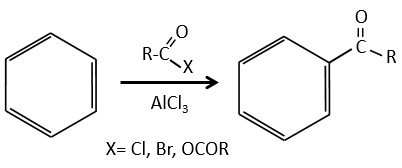
Acylation of Friedel-Crafts
The difference between the alkylation and the acylation is that for the second one the electrophile is an acylium cation, leading to the addition of -C=O-R on the phenyl.
The acylium ion is obtained with the help on a Lewis acid
The rest of the process is identical.
However, there is no polyacylation because the carbonyl is a mesomeric and inductive captor, taking electrons from the cycle. It is possible to reduce the ketone with the reaction of Clemmensen or of Wolff-Kishner.
Regioselectivity
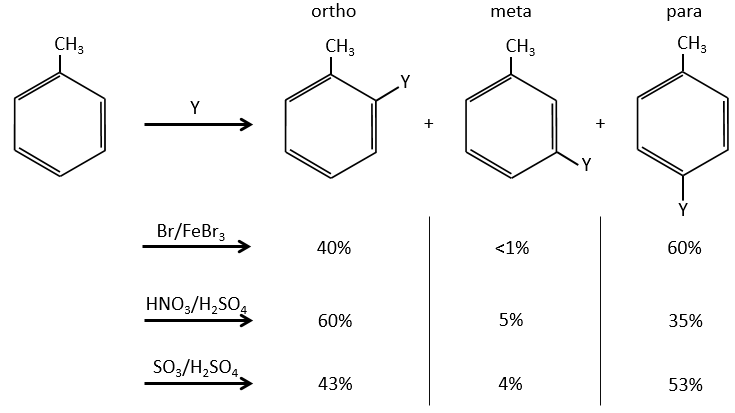
A benzene that already wears a group can be attacked on 3 non-equivalent positions: the ortho, meta and para positions. Some groups orient the reaction towards the ortho/para positions and other groups towards the meta position.
Mesomer effect
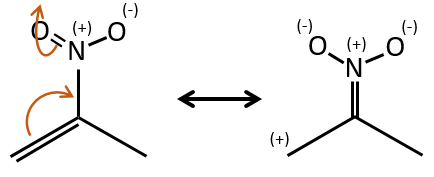
The mesomeric effect is the possibility for a heteroatom to share one lone pair with nearby atoms. For instance, O and N are mesomeric donors. They can stabilise carbocations by the sharing of one of their lone pairs that counterbalances the positive charge. They also enhance the nucleophile character of double liaisons. We note the mesomeric donors +M.
Groups can also be mesomeric acceptors and are noted –M. For instance the NO2 group is a mesomeric acceptor because it has a resonance form that can keep the additional charge.
Note that the oxygen can be mesomeric donor or acceptor depending on the group it is in and of the structure of the molecule.
Inductive effect
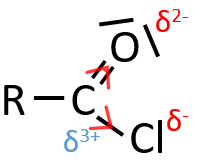
When two atoms are of different electronegativity, there is a displacement of electrons from the least electronegative atom to the most electronegative one. Groups or atoms can thus take or give some electrons from or to the nearby atoms. Atoms or groups that take electrons from the rest of the molecule are inductive acceptors and are noted –I. They destabilise carbocations and positive charge and can enhance the electrophile character of the atom they are bond with. For instance, the carbon of a carbonyl give a part of its charge to the oxygen and wears a partial positive charge δ+. A nucleophile is thus prone to attack this carbon.
An atom that is less electronegative than the carbon will give a part of its charge to the chain. They are called inductive donors and noted +I. The simplest inductive donor is H that is less electronegative than the carbon. However, H is taken by convention as the neutral intensity of the inductive effect. –CH3 is an inductive donor because the inductive effect of the 3 hydrogen’s is transmitted through the carbonic chain (over 2-3 carbons). As a result, the alkyl groups are inductive donors. The effect is stronger for -C(CH3)3 than for –CH3 because the amount of hydrogen atoms that can share their electrons.
The hybridation of the carbon is something to be taken into account to determine the inductive effect. The electrons in the s orbitals are more bound to the atom than the ones from the p orbitals. As a result, the electronegativity of sp2 carbons is slightly higher than the electronegativity of sp3 carbons.
Regioselectivity in function of the substituents of aromatic rings
The mesomeric and inductive effects are cumulative and a nitrogen in a NH2 group is simultaneously a mesomeric donor and inductive acceptor (+I-M). The mesomeric effect always prevails in intensity.
- inductive donors
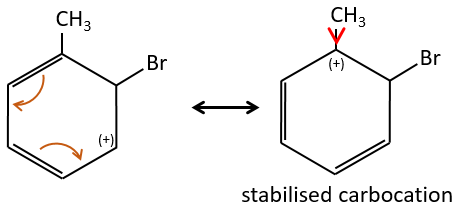
The groups that are donors of electron by hyperconjugaison (or inductive donors) are activating, i.e. favour the addition of new groups on the carbon. The substitution is oriented towards the ortho and para positions because the carbocation which has been made during the first step of the substitution can be stabilised by the inductive donor.
It is not possible to place the positive charge on the spot of the group if the substitution was to be made on the meta position. Usually, the para position is favoured to the ortho position because of the steric hindrance. However some groups such as NO2 seem to show more interest on the ortho position.
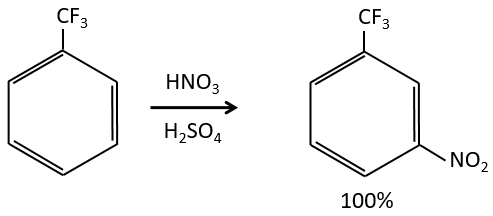
- inductive captors
Inductive electrocaptors are deactivating and orientate the reaction in meta. The reason is that in the other two positions, the carbocation can be at the feet of the CF3 group that wants to take more electrons, destabilizing furthermore the carbocation.
- mesomeric donors
Mesomeric electrodonors are activating and orientate the reaction in ortho/para because there is an additional resonance form.
Note that NH2, as well as the oxygen from the ether, is a mesomeric donor and an inductive captor. The mesomeric effect is always more important than the inductive one.
- mesomeric captors
Groups that are electrocaptor by resonance are deactivating and orient the reaction in meta.
- halogens
Halogens are deactivating but orient the reaction in ortho and para.
The steric hindrance here is very important and explain the difference of population between the ortho and para reactions.
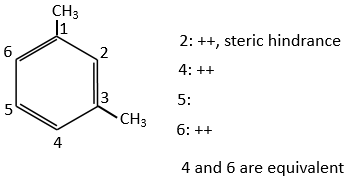
If there were two groups on the phenyl, the effects are additive and the substitution is made on the most activated/ less deactivated positions.
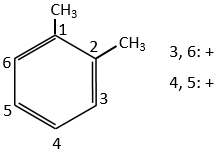
Both methyl groups of the xylene (dimehtylbenzene) shown above are activating and orientate in ortho/para. As both groups are activating, this reactant is more reactive than the toluene. The positions 2, 4 et 6 are thus favoured. The positions 4 and 6 are slightly more probable because there is less steric hindrance. In the case of the following xylene, the slots are almost equivalent.
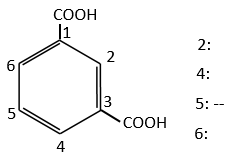
In the case of deactivating groups, the same reflexion is made. The COOH’s orientate in meta and the position 5 is the least deactivated position.
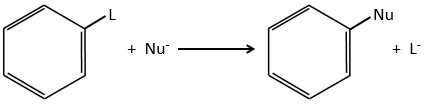
Nucleophilic substitutions
The nucleophilic substitution on aromatic rings is slower than the electrophilic substitution and that substitutions on sp3 carbons.
The reason is that the cycle is already full of electrons. Moreover, a sp2 carbon is more electronegative than a sp3 carbon. It is thus difficult to add a nucleophile (that loves positive charges) on a phenyl and the presence of a captor group on the phenyl is required to stabilise the carbanion. The leaving group has to be a good one.
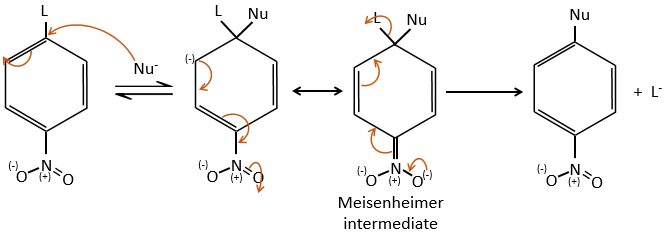
Several mechanism are possible to add a nucleophile on an aromatic substrate. One of them is the Addition-Elimination.
The activating group (NO2 here), is necessary to stabilise the negative charge of the carbanion formed during the first step of the reaction which is the slowest one. The intermediate complex is called intermediate complex of Meisenheimer.
The halogen (as leaving group) reactivity sequence is opposite to the one for SN2. On an aliphatic chain, the cleavage of the C-X liaison is made during the determining step of the SN2. On an aromatic, the cleavage doesn’t take place during the determining step. Moreover, the halogens take electrons from the cycle and the small halogens are thus more reactive than the big ones. As a result, we have the following reactivity sequences:
Aliphatic: F<<Cl<Br<I
Aromatic: F>>Cl>Br>I
A heterogeneous atom in the cycle (O or N) can play the role of the captor group.
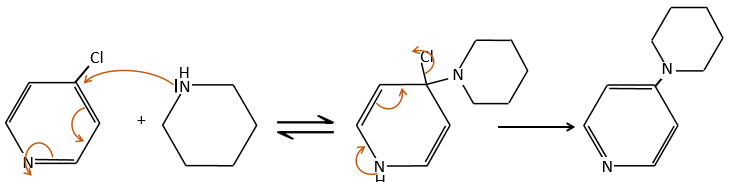
An application of this mechanism is the determination of the terminal amino acid of peptides. The peptide reacts with an aromatic compound through its terminal amine group.
Once the two substrates are bound together, we hydrolyse the peptide bonds (i.e. the amides). All the amino acids are now separated but only one of them is bound to the aromatic group.
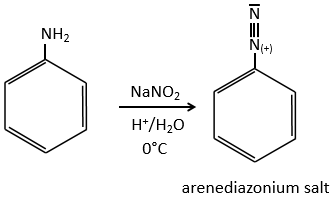
SN1 mechanism
This mechanism is mostly used to produce salts of arenediazonium. This species is obtained from aniline C6H7N with NaNO2 in an acidic environment.
The mechanism is the following:
Arenediazonium salts are stables at low temperatures and lose N2 at higher temperatures, freeing a phenyl cation that can react with a nucleophile.
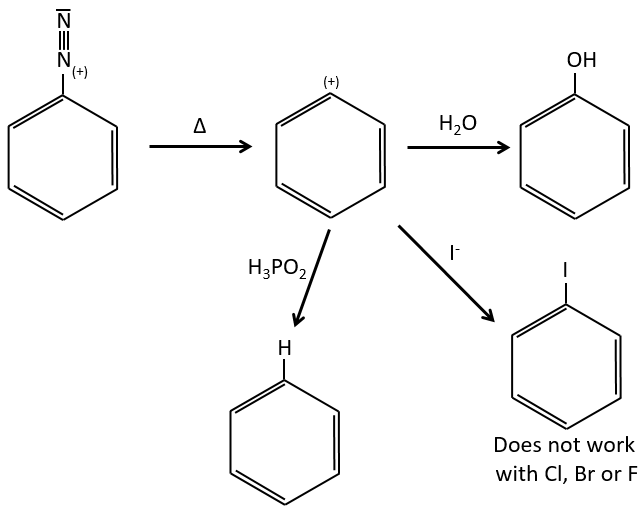
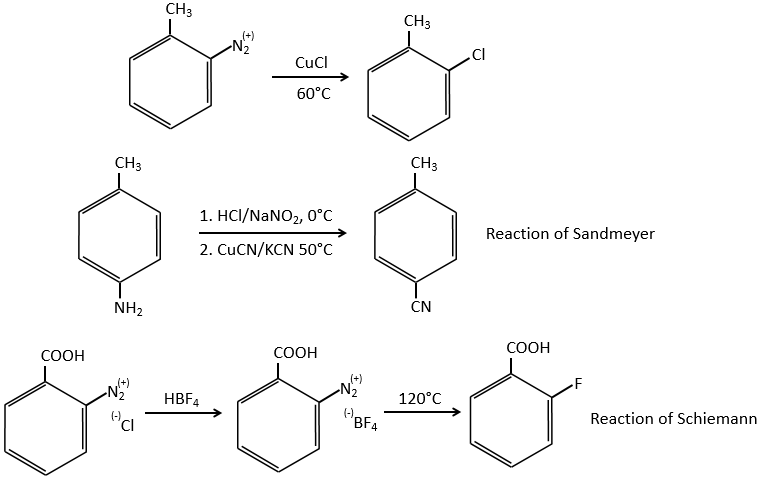
Other halogens than iodine don’t give good results because of secondary reactions. To add Cl, Br or F on an aromatic cycle, we use the Sandmeyer reaction, using copper salts like CuCl, CuBr or CuCN. The mechanism is a bit more complex and involves radicals.
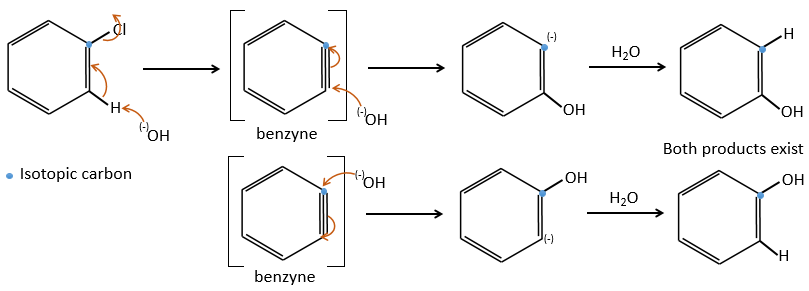
Mechanism involving a benzyne
Normally, halogenoarenes cannot make usual SN2 or SN1 reactions. However, in very harsh conditions of temperature and of pH, it is possible to force such reactions.
The mechanism involves a triple liaison in the cycle, the species being called a benzyne, The existence of this intermediate has been shown by an isotopic labelling. The C bound to the halogen is an isotope and we observe a racemic melange as product:
Chapter 2 : Organic chemistry – Exercises
This section is a full part of the course and contains some reactions that were not addressed in the main course. It is challenging to understand by yourselves some mechanisms with the hints that are in the exercises. If you don’t succeed, don’t worry. The solutions and the description of the reactions are directly following each exercise. However, the parts that have been seen in the course are considered as known and may not be explained in details.
The principle of the following exercises is pretty simple (but the exercises are not): We give you a series of reactions that are following each other but we will only give you some of the reactants and/or of the products. From them you have to reconstruct the whole process and find out which molecule and which structure hide behind which letter.
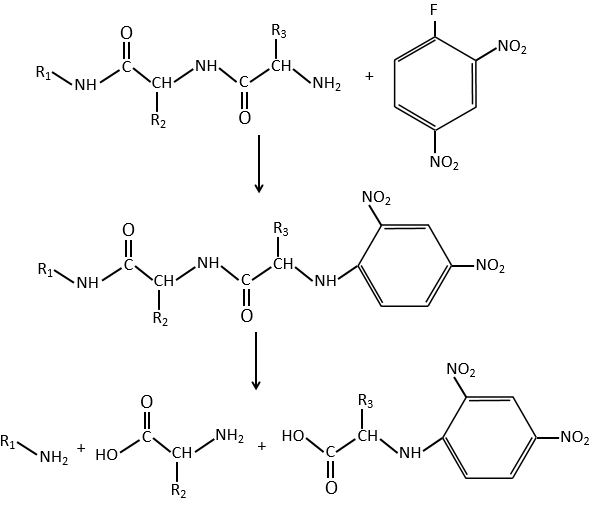
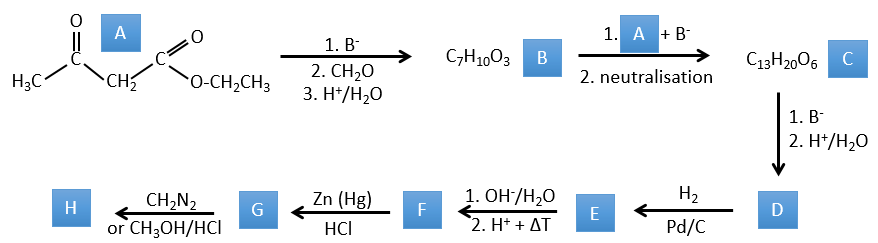
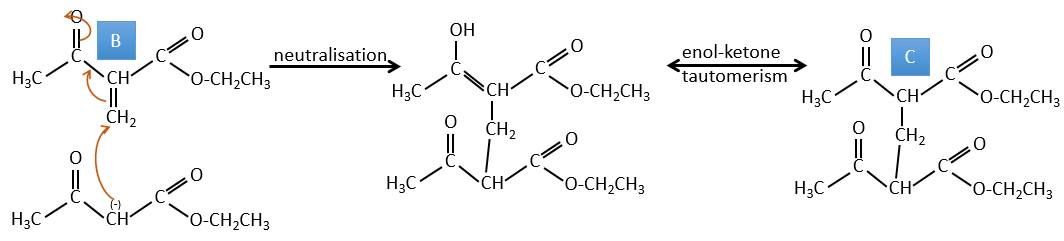
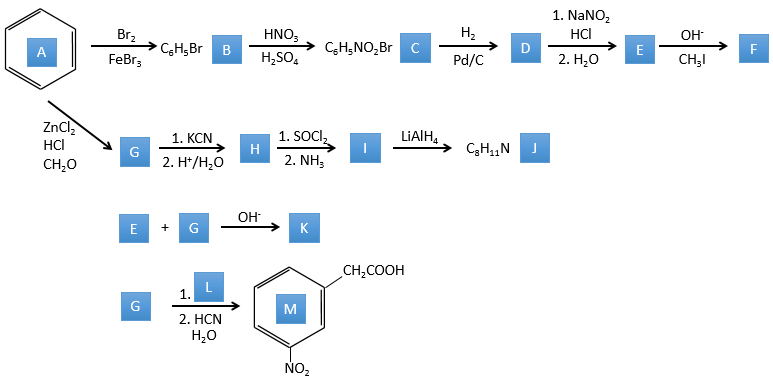
1. In this first exercise you have the structure of the initial reactant (A) and the composition of the first product B. You have to determine the structure of B, the product obtained by the first reaction. Then from B you have to determine the structure of C, then the compound D and its structure, etc.
Correction
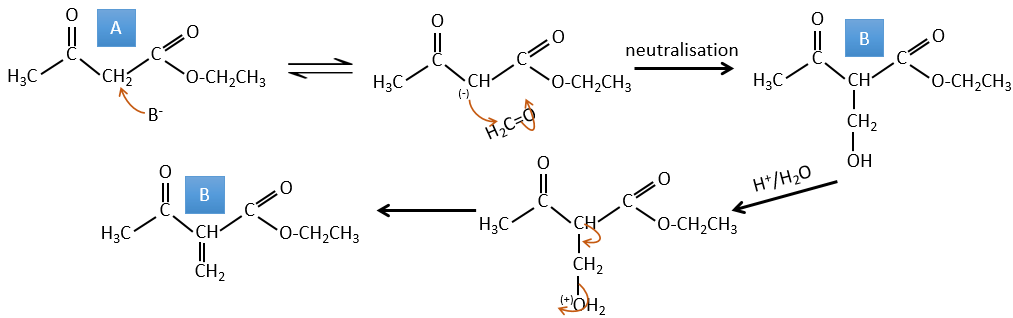
A→B: Two sets of protons are more acid than the others: the protons in α of carbonyl. The protons from CH3 are less acid than the CH2 because CH2 is between two carbonyls. It is thus there that the base attacks. The negative carbon attacks next the formaldehyde. A rearrangement occurs after the neutralisation to obtain B and H2O.
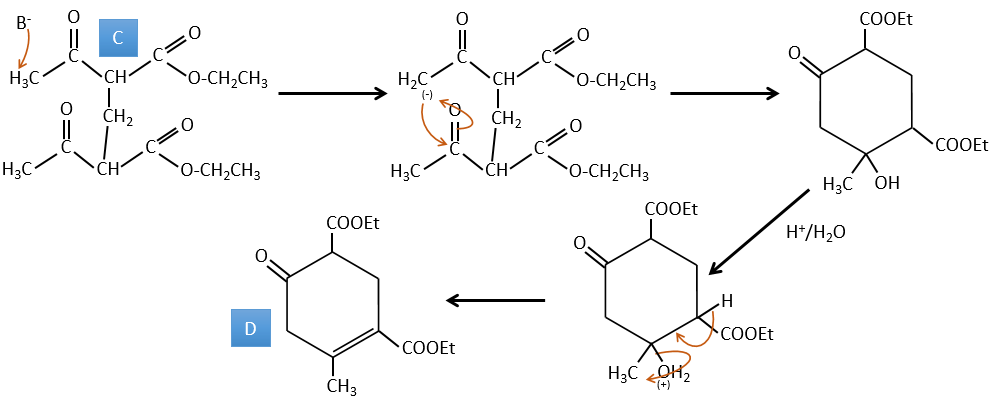
B→C: The first step is identical than for the previous reaction and the two molecules merge together. The attack is done on the sp2 carbon and we obtain a structure that is stabilised by a H bond forming a cycle between the OH and the C=O.
C→D: This time the proton (denoted *) is not attacked by the base because removal of one methylic proton allow the formation of a cycle of 6 carbons. In the second step, the acid catalyses the loss of a water molecule to obtain a double liaison conjugated with the carbonyl.
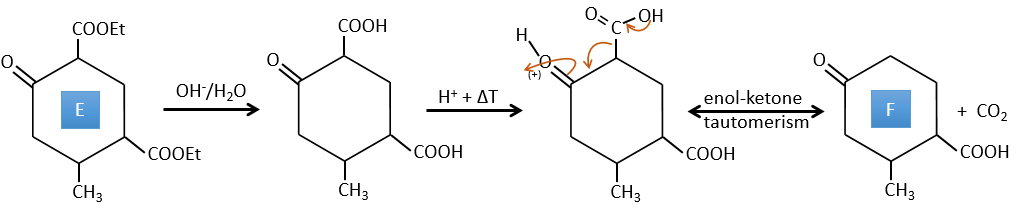
D→E: The double liaison is reduced to obtain a cyclohexane.
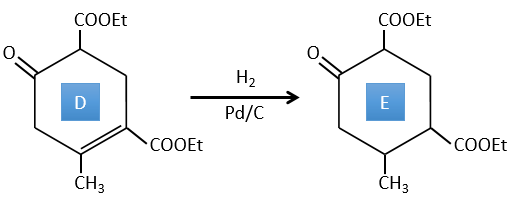
E→F: The esters are turned into carboxylic acids with a basic catalysis. CO2 is lost if we increase the temperature.
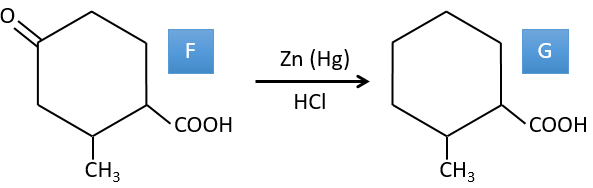
F→G: Zn reduces selectively a ketone into an alkyl chain.
G→H: The diazonium carbene (check nom) is able to take the proton from the acid. The carboxylate attacks next the carbene to form a methyl ester and to free N2. CH3OH leads to the same result but the process is different: There is a nucleophilic substitution on the carbonyl to replace -OH by -OCH3.
2. This exercise focuses on reactions on aromatics and on carboxylic acids and their derivatives.
Correction
A→B: The electrophile character of Br has to be enhanced by an acid of Lewis to do the reaction.
B→C: A nitro group is added to the cycle. There is already one substituent on the cycle so we have to determine if the nitro group is added in ortho, meta or para. A halogen orientates the reaction on the ortho/para positions. The para position should be favoured because of the steric hindrance on the ortho position.
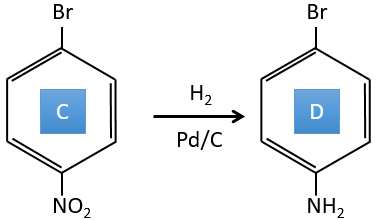
C→D: the reduction is limited to the nitro group that turns into an amine. To reduce completely the aromatic ring we have to heat up the solution to 300°C.
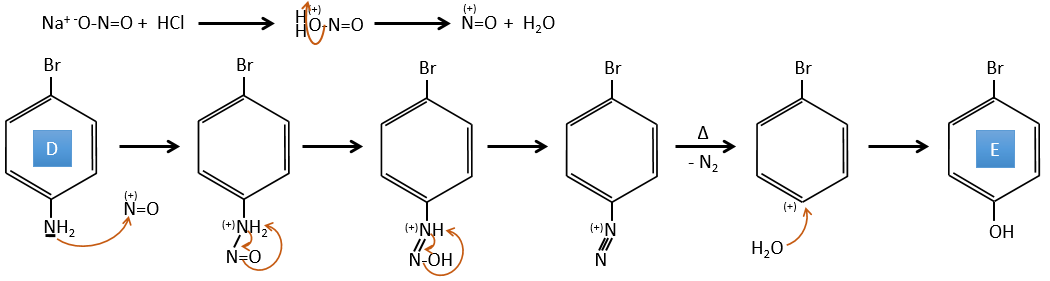
D→E: NaNO2 does not add a nitro group on the ring. It leads to the removal of the amine and the formation of an arenium. This very reactive species reacts with water to replace the amine by a hydroxyl group –OH.
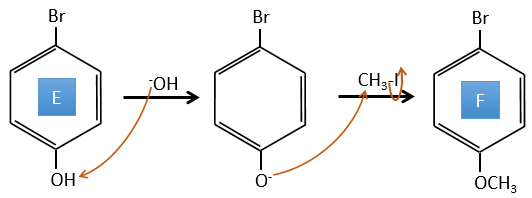
E→F: The base takes the proton of the p-bromophenol. There is then a nucleophile attack by the anion on CH3I to obtain the p-bromometoxybenzene.
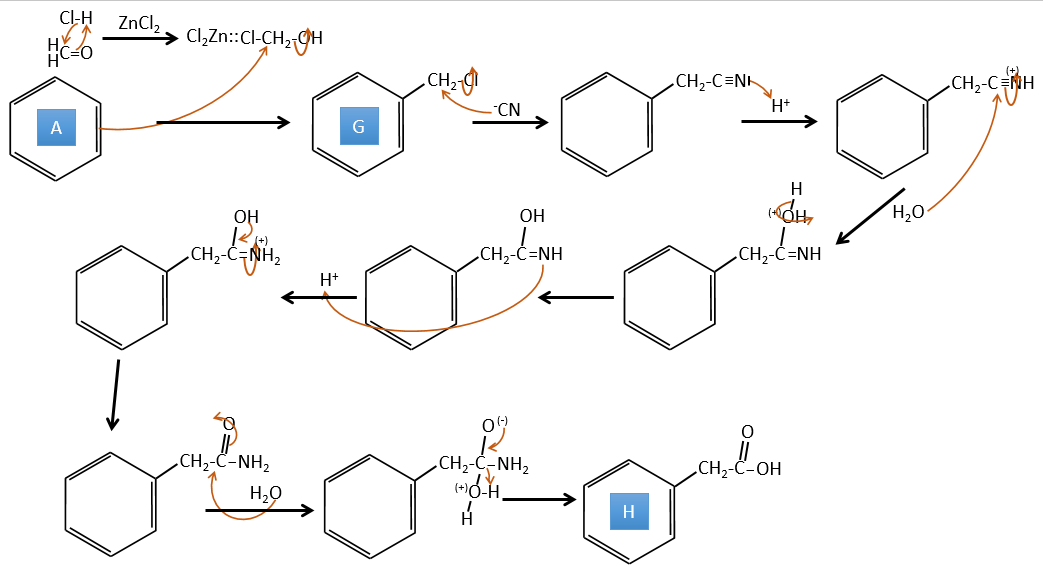
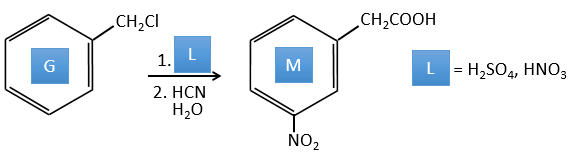
A→G: It is the chloromethylation reaction. During this reaction, the formaldehyde and the chlorydric acid form a chloromethanol stabilised by ZnCl2. The acid protonates the alcohol and the ring can attack it to reject water and bind CH2Cl.
G→H: A simple SN2 by CN– followed by its transformation into a carboxylic acid. This transformation is done by successive attacks of water molecules on the carbon bond to the nitrogen.
H→I: SOCl2 is a molecule that allows us to obtain an acyl chloride from an acid. It cannot be done with HCl or Cl2 because Cl– is a better leaving group than OH–. The reaction is followed by the formation of a primary amide.
I→J: The amide is reduce into an amine by LiAlH4. LiAlH4 can generates H– that attacks the carbonyl.
E+G→K: A base takes the proton from the bromophenol to obtain a stronger nucleophile. A SN2 takes place between the two species to merge them into one molecule.
G→M: The second step of the reaction leads to the formation of the carboxylic acid as it was the case in the reaction G->H. The missing element on M is the nitro group in meta. This position is favoured because of the mesomeric captor effect of the COOH through the CH2. The effect is however smaller than for a mesomeric captor directly in contact with the aromatic ring.
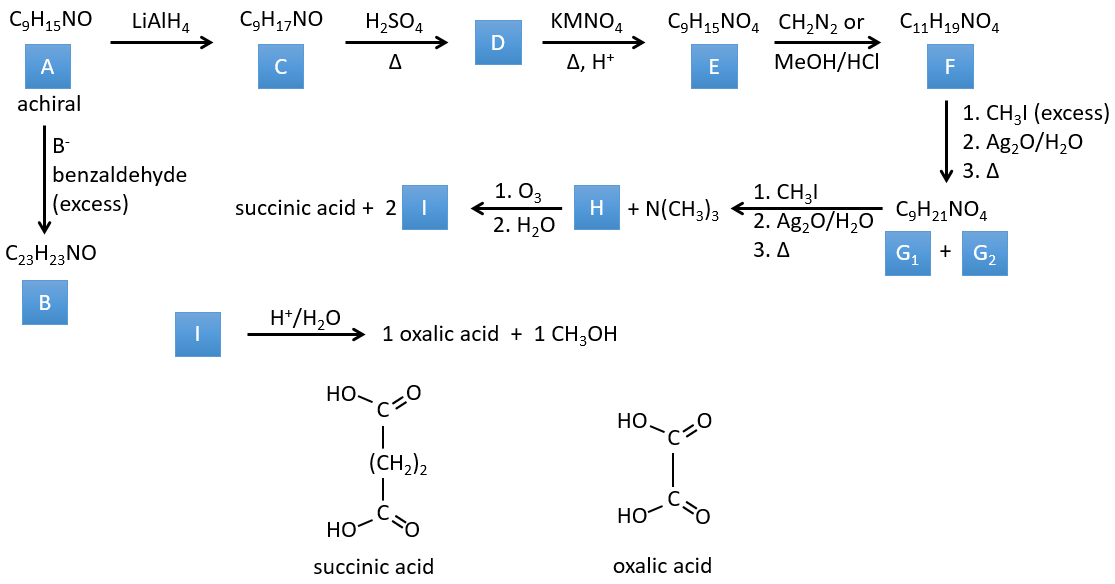
3. In this exercise the last product of a long series of reaction is given. It is the direct product of a reaction of ozonolysis. You have thus to go backwards in the reactions, starting from the end to find the reactants of each reaction. The formulas of most of the molecules are given. G1 and G2 are isomers.
Correction
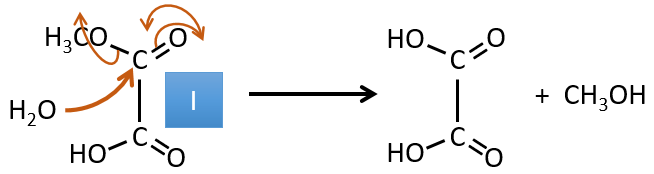
I→…: One of the products, the oxalic acid, is a carboxylic acid and one reactant is the water. We can thus guess that the reaction is a reaction of substitution on a derivative of carboxylic acid. The other product of the reaction is one methanol molecule. One carboxylic acid was thus an ester before the reaction. Only one methanol is generated by the reaction so only one of the two acids of the oxalic acid was an ester.
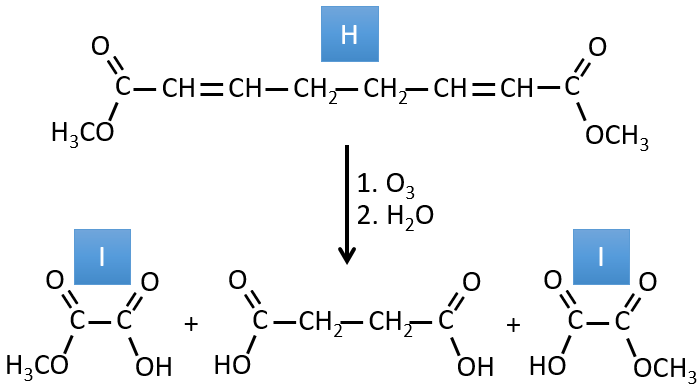
H→I: The ozonolysis cuts a molecule at double liaisons and leads to the formation of carboxylic acids in presence of an oxidant. There are 4 acid groups in the products of this reaction and 2 esters. The 4 acid groups indicate that a bigger molecule was cut down at two places. The double liaisons were thus conjugated with the esters. It is thus an example of reaction that involves a part of the conjugated system and not all of it. We don’t know if the double liaisons are cis or trans.
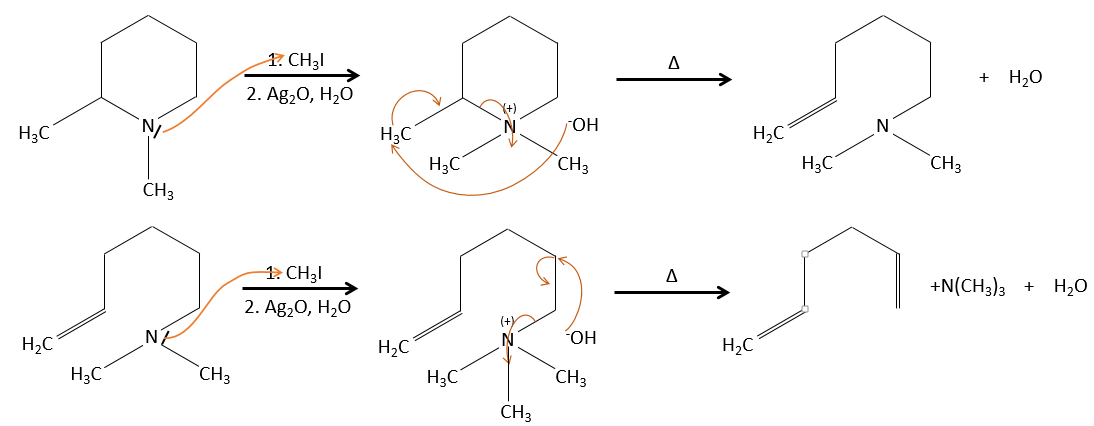
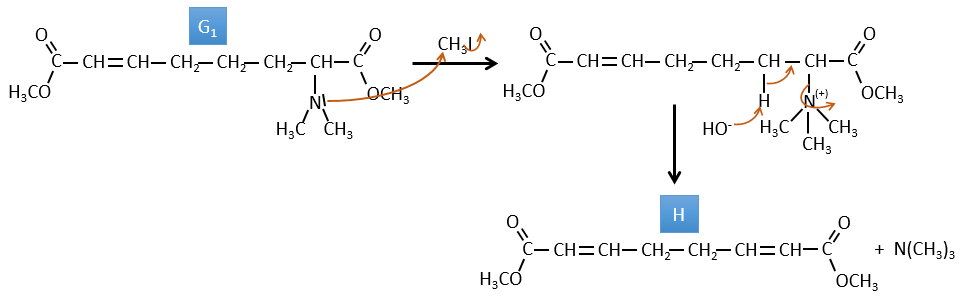
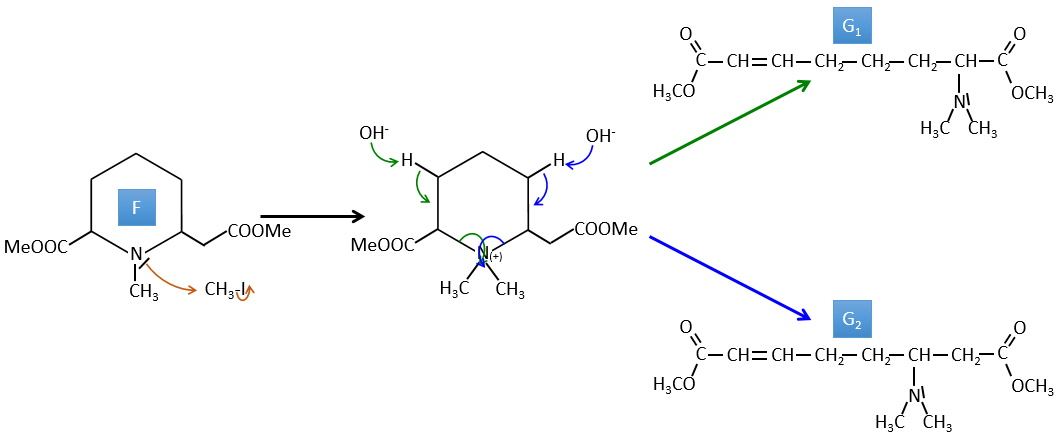
G→H: G1 and G2 are two isomers. There are two other information that we may consider to find the isomers. CH3I, Ag2O and delta are the reactants of the Hoffmann reaction. This reaction breaks one C-N bond and forms a double liaison on this carbon. It is thus one of the pi liaisons that the nitrogen was bound. The second information is that the nitrogen is no more on the product, meaning that it had only one liaison with the chain. The second product of the reaction, N(CH3)3, confirms that. The two isomers are thus different from the carbon on which N(CH3)2 was bound. It can be the carbon in α or in β of carbonyl.
F→G: It is the same reaction than G->H but the nitrogen is still on the molecule after the reaction. It means that it was bound somewhere else on the molecule. The location is where the pi liaison stands. The molecule had thus a cycle of 6 atoms prior to the reaction. Contrarily to the species H, the cycle F is not symmetric. It is why we can obtain two isomers G1 and G2.
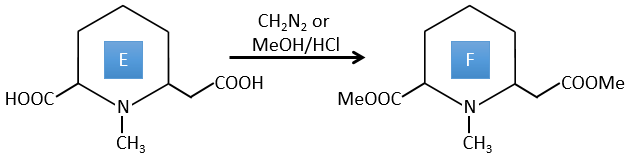
E→F: CH2N2 and MeOH/HCl are two techniques to replace a carboxylic acid by a methylic ester. The species E has thus two carboxylic acids.
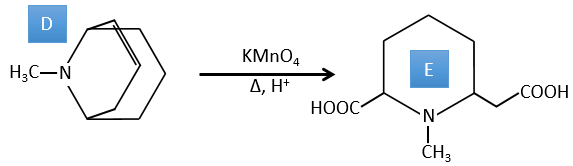
D→E: KMnO4 acts like the ozone. The two carboxylic acids were thus forming one bridge of the cycle. This bridge also forms a cycle of 6 atoms at the side of the nitrogen (and a cycle of 8 carbons with the other side).
C→D: If we check the compositions of the reactant C and of the product D, we see that there is a difference of H2O. The role of H2SO4 was thus to remove this molecule of water from C with the formation of a double liaison. The hydroxyl group could be at two places (in α or β of the bridged carbons). At this point, we cannot say which position is correct but the reaction A->B is only possible with the hydroxyl group in β of the bridged carbon. The species is thus symmetric and achiral as is the species A.
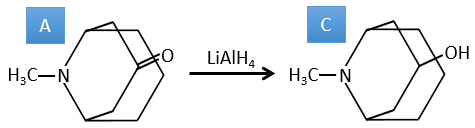
A→C: A classic reaction of reduction. A gets H2 in the process and we can assume that the hydroxyl group was a ketone before the reduction.
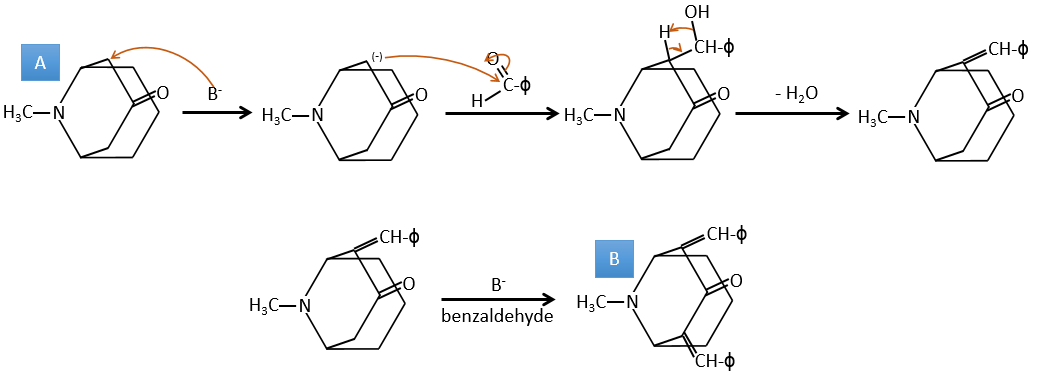
A→B: The base is there to remove a proton in α of carbonyl. Those protons are acid in reason of the tautomerism enol-ketone. The carbanion attacks one benzaldehyde on its carbonyl and water is lost after this attack. The double liaison is in α of carbonyl and forms a long resonance chain with the phenyl. This reaction can be repeated on the other side of the carbonyl to obtain the product B.
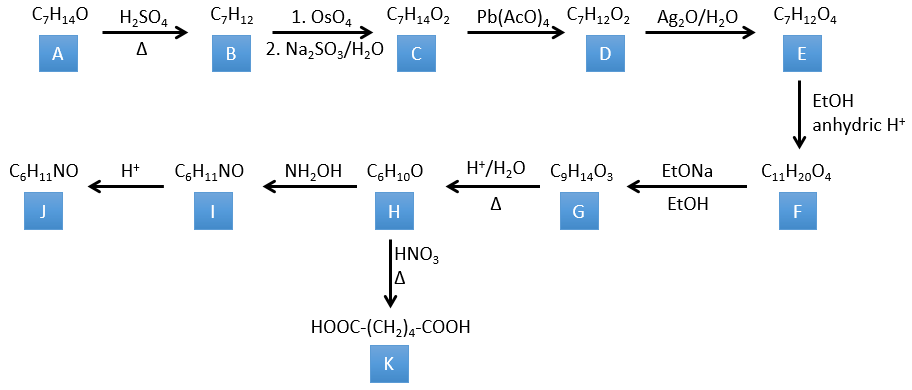
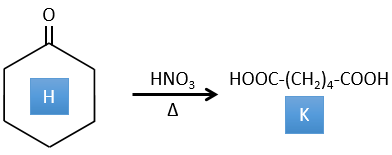
4. There are a few specific reactions in this exercise (mainly BàE). You have the formulas of all the compounds but only the structure of the compound K to start with. HNO3, ΔT is a reactant that breaks the C-C liaison of a ketone to obtain two carboxylic acids. The mechanism is unknown.
Correction
H→K: As explained in the wording, HNO3 breaks a ketone into two acids. As the two acids are present in the product, H is a cycle with a ketone on it. The cycle has 6 carbons.
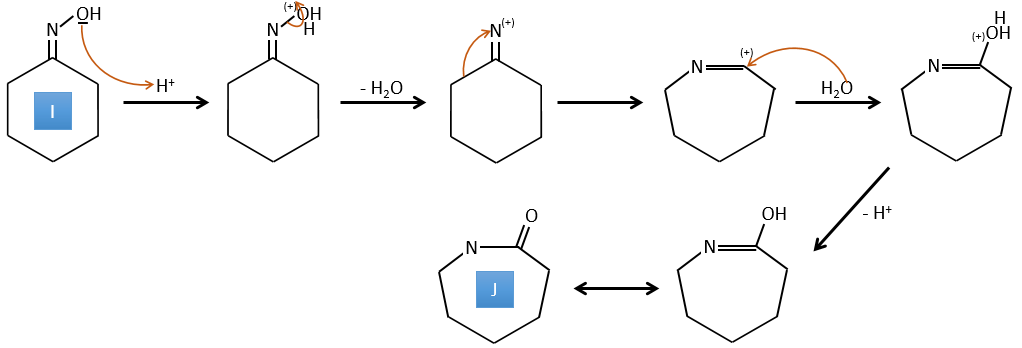
H→I: This reaction leads to the formation of an oxime, i.e. a base of Schiff where R=OH. The mechanism involves a nucleophilic substitution by the nitrogen on the carbonyl to reject one water molecule.
I→J: This reaction is the transposition of Beckmann. Under acid conditions, the OH of the oxime is protonated and water is freed. The cationic nitrogen is attacked next by a carbon in alpha of the oxime, placing the nitrogen into the chain. The water comes back to attack the carbocation and to form an amide.
G→H: A simple reaction to change an ester into a carboxylic acid. The group is then removed from the molecule by an elevation of temperature.
F→G: A proton in α on carbonyl is taken by the strong base. The formed anion attacks next the ester to form a cycle of 6 carbons wearing one ketone and one methylic ester.

E→F: The carboxylic acids are replaced by methylic esters.
D→E: Ag2O is able to oxidize an aldehyde into a carboxylic acid.
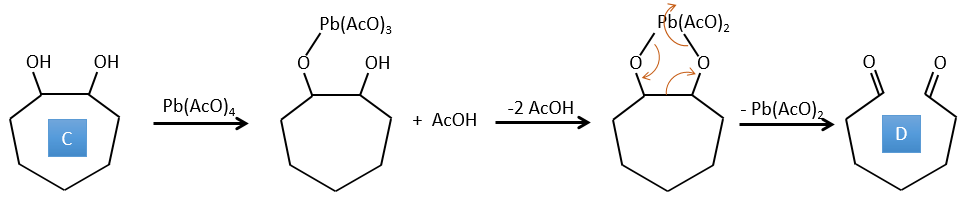
C→D: Pb(AcO)4 is a compound that reacts with cis-glycols. Pb exchanges one equivalent of acetic acid to bind with one oxygen. The process is slow but it will also bind with the second OH to form a cycle of 5 atoms. This cycle breaks to generate 2 ketones that are now separated. The same mechanism is obtained with HIO4. As there is only one product, the he reactant is thus a cyclic cis-glycol.
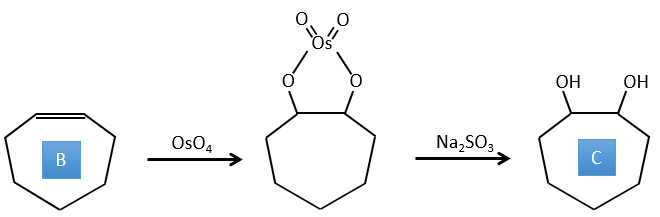
B→C: The osmium tetroxide is a reactant that affects specifically C=C and that generates an osmic ester, a bit like the complex formed by Pb(AcO)4 with the cis-glycol. Na2SO3/H2O removes the osmium from the molecule to obtain the cis-diol. KMnO4 can do the same but we have to be in basic and cold conditions or we will obtain a diacid. The reactant is thus a cycle of 7 carbon with a double liaison between two of the carbons.
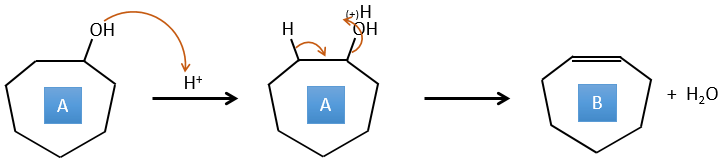
A→B: This reaction is simply the removal of a molecule of water from the cycle that gives a double liaison. We can deduce this from the difference of composition between the reactant and the product: C7H14O-C7H12=H2O.
Chapter 4f: solids – conductivity
Electric conduction
Some solids are conducting the electricity and some are not. We will explain here from where the conductivity comes and the difference between a conductor and an insulator. The conductivity is explained by the band theory.
We have seen in the section on molecular orbitals that liaisons are the combination of the atomic orbitals of the bound atoms.
The width of the band increases with the number of atoms but the difference of energy between the molecular orbitals decreases significantly and in metals, the atoms are all bound together, leading to a continuum of molecular orbitals, a band.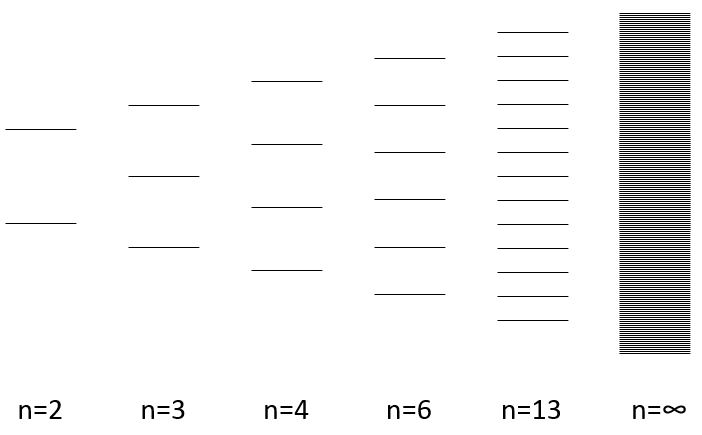
The energy required to an electron to jump from a lower orbital to a higher one is thus small inside the bands and a simple thermic agitation may be enough.
The bands can extend on a wide range of energy but there can be some space between two bands of molecular orbitals. The ranges of energy not covered by any band are called band gaps. In some cases, there is no gap between two bands: the bands overlap.
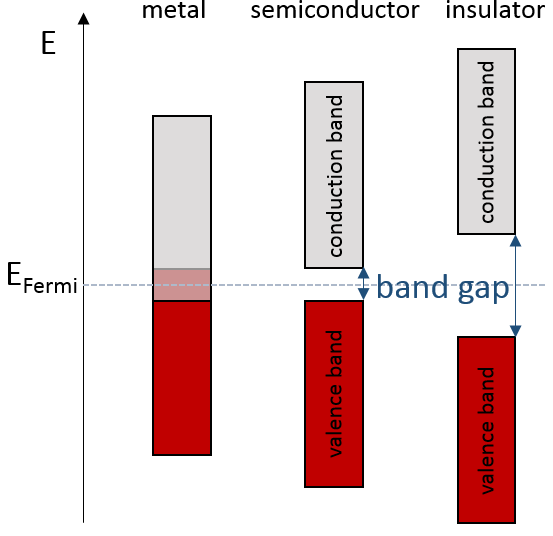
The electrons in solid respect the Pauli principle of exclusion: lower energy levels are filled first and by pairs of electrons. The highest occupied molecular orbital is called HOMO and the lowest unoccupied molecular orbital is called LUMO. The HOMO and LUMO can be in the same band or in bands separated by a gap.
The Fermi–Dirac distribution f(ϵ) gives the probability that (at thermodynamic equilibrium) an electron occupies a state having an energy ϵ.
T is the temperature, k is the Boltzmann constant and μ is the total chemical potential. The chemical potential is a form of potential energy that can be absorbed or released during a chemical reaction or a phase transition.
If there is a state at the Fermi level (ϵ = µ), then this state will have a 50% chance of being occupied at any given time. It is in the vicinity of the Fermi level that we find the LUMO and HOMO orbitals. The conductivity of a solid will depend on the ability of electrons to pass from a HOMO to a LUMO orbital. In a metal, the Fermi level is in a band and it is thus very easy for electrons to jump from the HOMO to an unoccupied orbital. Also remember that in metals, some electrons are not bound to atoms but are shared and can move inside the solid. For those reasons, metals conduct well electricity.
The Fermi level in semiconductors is in a small gap. It is then necessary to give an additional energy, equivalent to the energy gap, to the electrons to make them reach the LUMO. The band just beneath the Fermi level is called the valence band because the electrons of valence are in this band at the equilibrium. The band just above the Fermi level is called the conduction band. A semiconductor conducts electricity when electrons can jump from the valence band to the conduction band. In an insulator, the gap is larger and it is thus difficult for electrons to reach the conduction band.
Superconductivity
Considering this, an increase of the temperature leads to a better conductivity. However, it is not always true. Superconductors are particular materials the resistance of which drops to zero when they are cooled below a critical temperature, that can vary depending on the material of the superconductors. It is a quantum mechanical phenomenon characterized by the Meissner effect: when a superconductor is placed in a weak external field and cooled below the critical temperature, the magnetic field can no more penetrate the material (in fact, it does but only on a very small distance). In the superconductors, the electrons are bound by pairs, called the Cooper pairs. Despite the repulsion that we may expect between two electrons, an attraction can exist at very low temperatures due to the electron-phonon interaction. A phonon is a mode of vibration of the atoms of the lattice. The vibration has a given frequency and thus an energy (E=hν). The electrons of a Cooper pair are not necessary close together because this is a long range interaction. This interaction is very small but when we consider many pairs of electrons, the pairing opens a gap in the allowed energy states of the electrons. This gap prevents small excitations of the electrons, what leads to the zero electrical resistance and to the superconductivity.
Superconductors are also the most powerful electromagnets know. Those are used in several applications. One of them is the fastest train on earth, the Maglev, that uses superconductor magnets to levitate several centimetres above the rails.
Thermal conductivity
The thermal conductivity is the quantity of heat that propagates through a material by unit of time. The bigger the thermal conductivity, the better a material conducts heat. An insulation product has a low thermal conductivity. A thermal conductivity of 1 Wm-1K-1 is the quantity of heat that propagates over 1 second through a bloc of material with a surface of 1m2 and a width of 1m when a difference of temperature of 1K is applied between two opposite faces of the material.
The heat propagates from the hottest location towards the coldest location. That may sound obvious, but when we touch something cold, the cold does not comes from the cold object to us, we give heat to the cold object.
When we are cooking, the handle of pans are insulated so that we can grab them without burning our hands. The pan itself has to be a good conductor of heat.
Flaws in crystals
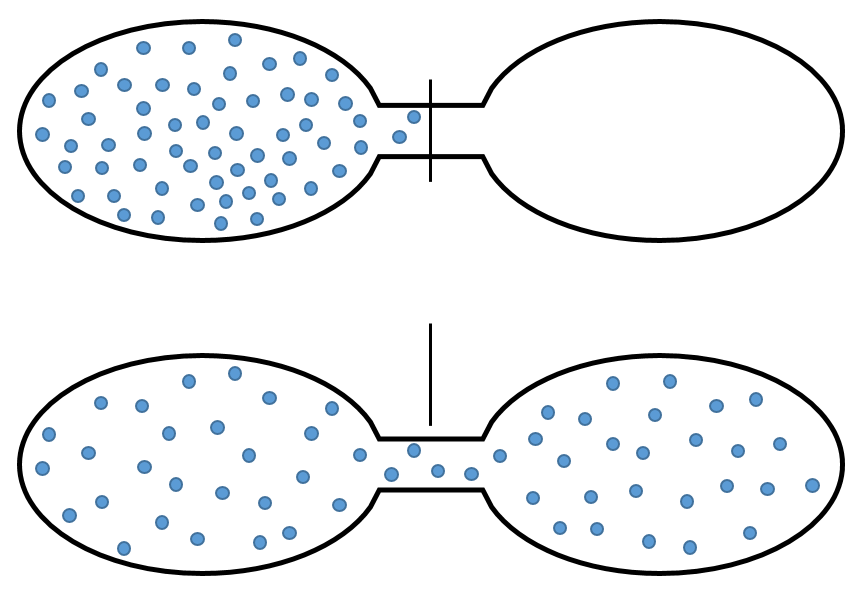
The arrangement in a crystal is rarely perfect. In fact, except at 0K, solids have flaws in their arrangement. It is a result of the second law of thermodynamics (next chapter) that says that the disorder of the universe has to increase during any process. A flaw in a crystal increases the disorder in the crystal: there is only one way to draw one perfect arrangement of atoms but there are many possibilities to place a flaw in this arrangement.
As a result, the single perfect crystal is at the absolute zero. For larger temperatures, the crystal has some energy from the heat that is turned into potential energy through flaws.
Different types of flaws exist:
- Punctual flaw: one individual atom is not placed correctly in the arrangement. Several cases can be sorted:
- One atom is missing in the arrangement: it has been expelled from the core of the crystal to its surface. It is called a flaw of Schotty.
- One atom is at the wrong place: the atom is still in the core of the crystal but not aligned with the other atoms. It is called a flaw of Frenkel.
- One atom has been replaced by another one
- Linear flaws: one line of atoms is out of the arrangement.
- Planar flaws: it comes from the merging of two crystals growing in different directions.
Alloys
An alloy is a solid composed of several elements and having the properties of a metal. Different types of alloys exist:
Alloy of substitution: some atoms of the metal are replaced by other atoms of similar size. The stainless steel is an alloy of substitution for which some Fe are replaced by Cr and Ni, respectively in the proportions of 18% and 8%.
Interstitial alloy: Small elements are added in the interstices between the atoms of the network. If you remember, we have seen that there is a lot of empty space in crystals and small ions can be inserted in the holes between the atoms.
Mixt alloy: it is a combination of the interstitial alloy and of the alloy of substitution.
The properties of the alloys depend on the elements composing the alloy and can drastically change from the properties of the main metal. A metal like the aluminium that is flexible can become hard if we mix manganese with it. However, this mix makes the solid very sensible to water.
Doping of semi-conductors
Semi-conductors can be doped by the intentional addition of impurities in their structure. The impurities have the effect of adding or removing electrons from the lattice. In the case of additional electrons, those are destined to fill the band gap between the valence and the conduction bands. Removed electrons come from the valence band so that the gap is displaced.
The semiconductors of the column IVa are doped by elements of the columns IIIa or Va. The replacement of a Si by a P (Va) increases the amount of electrons in the lattice. It is also the case when an element of the column IIIa (as B) is inserted in the holes of the lattice. A doping where electrons are added in the lattice is called of type n (n for negative), or n-type. We also say that Si uses P as a donor (of electron).
Elements of the column IIIa can also replace atoms of Si in the lattice. In this case, the lattice loses one electron by replaced atom. The inserted atom, Al for instance, has an electron less than the other atoms. It creates a “positive hole” in the lattice. A doping where electrons are removed from the lattice is called of type p (p for positive), or p-type. We also say that Si uses Al as a captor (of electron).
The semi-conductors or the other columns can also be doped the same way by elements of a lower or higher column.
Diodes
A p–n junction diode is made of a crystal of semiconductor, Impurities are added to it to create, on one side a region that contains electrons, forming a n-type semiconductor, and on the other side a region that contains holes, forming a p-type semiconductor. The boundary between these two regions, called a p–n junction, is where the action of the diode takes place. When those two materials are attached together, a flow of electrons occurs from n to p side. As the electrons flow there is now a region where no charge carriers (electrons and holes in this case) are present. This region is called the depletion region. The crystal allows electrons to flow from the n-type side (called the cathode) to the p-type side (called the anode), but not in the opposite direction.
Chapter 1 : Thermodynamics – First principle
The thermodynamics is the study of the transfer of energy and especially of heat. It is important to make the distinction between heat (q) and temperature (T). The temperature reflects the motion of particles and is connected to their kinetic energy, but the temperature is no energy. Heat is an energy that exist if there is a difference of temperature, by convention from the hottest to the coldest component. The units of the heat is the units of an energy, i.e. joules J=N.m.
When it comes to transfers of energy, we have to define the system in which we are working. The system is the part of the universe that we are analysing and we distinct it from the environment that is the rest of the universe.
3 kinds of systems can be differentiated
– Isolated system: there is no exchange between the system and the environment
– Closed system: exchanges of energy are possible between the system and the environment
– Open system: exchanges of energy and/or matter are possible between the system and the environment
A system is exothermic if it liberates heat. If it takes heat, the system is endothermic.
The thermodynamics is governed by 3 major principles.
First principle
Conservation of the energy: The energy of the universe is constant.
It means that a process occurring in an isolated system doesn’t involve any variation of energy. If exchanges of energy are allowed with the environment, i.e. in closed systems, the intern variation of energy in a system is composed by the heat q and the work W to make the process.
If the system also allows exchanges of matter, a term dEm representing the energy of the flow of matter is added.
The variation of energy is a state function. It means that this function does not depends on which way the system reached this point, but only on its initial and final state. W and q are not state functions and depend on the way the system evolves during the process.
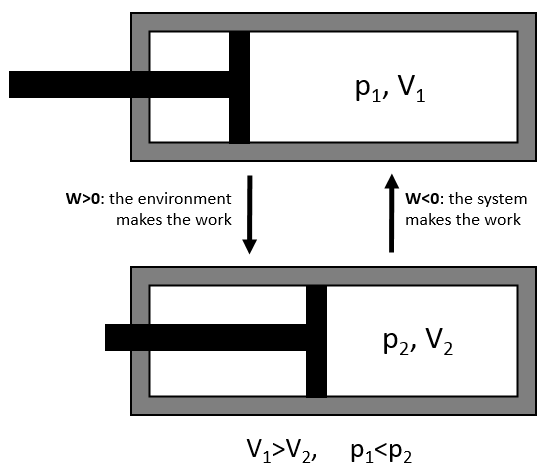
The work has a negative value if it is made by the system. For instance, imagine a volume in which a gas is stored.
To compress the gas, the environment has to apply a force on the piston. W is thus positive in this case. If the piston is free of movement, the gas in the volume applies a pressure on the piston to increase the volume of the system. In this case W<0.
The work is an energy, so it is basically a force multiplied by a distance. If we consider the dilatation of a perfect gas the work would be
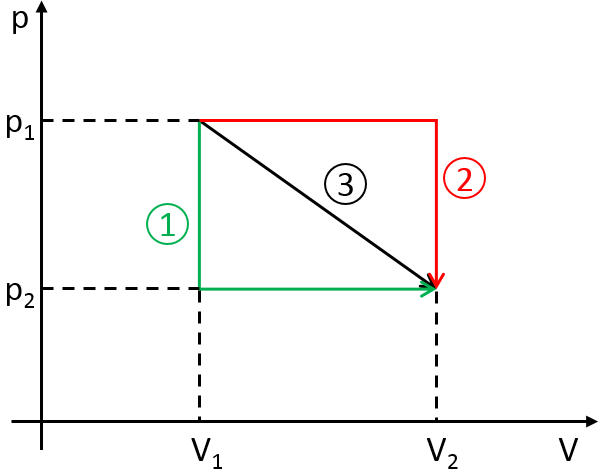
To move from a state (p1,V1) to (p2,V2) several paths can be taken.
Those ways are equivalent in the term of variation of energy because the energy is a state function: the final state and the initial states are characterised by an energy that does not depend on how they were obtained. Yet, the work and heat are different for each path.
Indeed, on the path 1, W=-p1(V2-V1). On the path 2, the work is W=-p2(V2-V1). As p2<p1, it means that more work is required on the path 1 and that there is a larger production of heat on the path 2. On the path 3, the volume and the pressure vary simultaneously. We use the law of perfect gas to determine the work in this case. Path 3 is in fact an isothermal curve, where q=0.
Now, let’s talk about heat. In previous chapters, we discussed about the heat capacity. It is the energy required to increase the temperature of the substrate by one kelvin/degree. We distinguish the heat capacity at constant pressure Cp and at constant volume CV.
Note that we used partial derivatives ∂/∂T instead of derivatives d/dT. A partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant.
H is the enthalpy of a state and ΔH is the variation of enthalpy of the process (that can be a reaction or a transition of phase for instance) at a constant pressure. ΔH is thus equivalent to qp, the subscript p indicating that it is the heat at p=cst.
The equation for the enthalpy is
For perfect gases, pV=nRT, so
Given that Cp= ∂H/∂T we find a relation between Cp and CV for perfect gases
For solids and liquids, the variation of volume is negligible and Cp»CV.
Calorimetry
An enthalpy of reaction ΔH° is associated with each reaction.
The ° indicates that this value is the enthalpy found for one mole of reactant, at 1atm. The enthalpy of a reaction can be measured experimentally by calorimetry. During calorimetry, a reaction is made in an isolated system (no exchanges with the environment). The variation of temperature in the system is measured and from this measure we can deduct the heat of reaction. For instance, the neutralisation of HCl by NaOH is exothermic (ΔH°<0), meaning that this reaction generates heat. It is thus possible to measure a variation of temperature ΔT during the reaction. To do so, we use an isothermal and closed recipient in which the reactants are initially separated. The temperature in the system can be read on a thermometer. The temperature is not directly taken in the reactive solution. Usually, the reaction takes place in a recipient (called the calorimetric bomb) that is surrounded by water. The whole setup is in the isothermal recipient. The variation of temperature is measured in the water. When the reaction takes place, the elevation of temperature is recorded in function of the used amount of NaOH. With the adapted setting, we can measure qp (p=cst) or qV (V=cst).
If the pressure is kept constant, the variation of temperature ΔT is proportional to qp.
As we consider a liquid phase, qp»qV.
CV can also be determined experimentally: A given heating is applied in the solution through an electric resistance.
With V the tension and R the resistance. The variation of temperature ΔT due to this heating depends on the heat capacity of the liquid.
So if we know the applied tension and the resistance, the measure of the variation of the temperature gives us the value of Cv.
Law of Hess
The energy and the enthalpy are state functions, i.e. their value does not change in function of the path/process and are only a function of the state of the system. It means that if we perform a cycle of transformations, obtaining at the end our initial compounds, the sum of the variations of enthalpy of the processes of the cycle is equal to 0kJ/mol. Note that the absolute value of the enthalpy of a body cannot be determined. Only variations of enthalpy can be determined. It means that we can determine the value of enthalpies with regard to a given process and thus that the enthalpy of formation of a molecule is determined in comparison with other reactions.
By convention, the enthalpy of formation of simple bodies composed of one single element (for instance O2, H2,Na,etc but H2O not because there are two different atoms in the molecule) in their standard state equals 0kJ/mol. The standard state is the most stable state of a body at 25°C and 1 atm. In the nature, some elements can be found in several states but the body in its normal state at 25°C and 1 atm alone has a ΔfH°=0kJ/mol. For instance, the carbon can be found as graphite and as diamond.
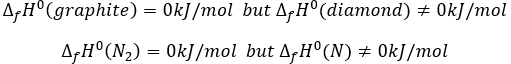
We say that the graphite and the diamond are two allotropes of carbon. The atoms are bond together differently in those two solids. Between them, the standard state of the carbon is the graphite because the diamond is not formed in this range of pressure and temperature. Technically, the notion of standart state depends on the temperature and pressure, and the diamond will be the standard state of carbon for very high pressures but we commonly use the “standart state” term for the normal conditions of temperature and pressure.
For molecules that are not in their standard form, the enthalpy of formation is the enthalpy of the reaction producing the molecule from the elements in their standard state that compose it.
The enthalpy of this reaction is thus the enthalpy of formation of the carbon dioxide CO2: it is the reaction that generates carbon dioxide from the elements in their standard state that compose CO2.
This reaction is the reverse of the formation of the methane CH4. The enthalpy of reaction is simply minus the enthalpy of formation ΔrH°=-ΔfH°.
The enthalpy of this reaction is twice the enthalpy of formation of the water because we form two moles of water with this reaction. The enthalpy of reaction is given in kJ by mole of product
If we combine those three reactions, we obtain the cycle of Hess. The enthalpy of this final equation is the sum of the enthalpies of formation of the three sub-reactions:
We can sum up the enthalpies of the sub-reactions to obtain the enthalpy of reaction of formation of CO2 and H2O from CH4 and O2.
In a general way, the enthalpy of a reaction is the sum of the enthalpies of formation of the products minus the enthalpies of formation of the reactants, each one multiplied by its stoichiometric coefficients.
We clearly see here that those two expressions are identical
Don’t forget that the enthalpy is a state function but depends on the temperature and that a reaction can be favoured by a variation of temperature.
At a constant pressure, the enthalpy can thus vary if there is a variation of temperature
A change of state will also increase the enthalpy of reaction.
If we want to change ice into vapour, i.e. sublimate ice, at a constant pressure=1atm,
the enthalpy will be
The triple point is a particular point where ice, vapour and water coexist and where
From that point, we can find the enthalpy of one phase transition from the other two.
Energy of liaisons
We have seen that we can find the enthalpy of reactions from the enthalpies of formations of each participant of the reaction. There should thus be reactions that allow us to determine the energy of chemical bonds. For instance, the reaction
is basically the scission of 4 C-H bonds. Nothing else has been done during this reaction. We can determine the enthalpy of the reaction ΔrH0 from the enthalpy of formation of CH4, C and H. We have seen earlier the inverse of the reaction of formation of the methane
From that reaction, we still need to dissociate the molecules of H2 and to sublimate the graphite into a gas.
As there are 4 C-H bonds that have been broken, each bond has an energy of 419kJ/mol.
Fuels
The thermochemistry is a vast domain of the chemistry that finds applications in fuels for example. We can determine the energy of liaisons during the combustion of molecules composing the fuel, exactly the same way as we did for the liaison C-H. The hydrazine N2H4 is a nitrogen molecule used as fuel for space propellers.
Most of the nitrogen compounds have a positive enthalpy of formation, meaning that we need to spend energy to generate them. It also means that they will easily break to form N2 and H2O, generating a lot of energy. An exception is NH3. What is the energy of the reaction? O2 and N2 are in their standard form, meaning that their ΔfH0=0kJ/mol. The enthalpy of reaction is thus
This reaction generates heat because the energy of the formed liaisons is greater than the energy of the broken liaisons. We broke 4 N-H bonds to form 4 O-H and the N-N bond became a triple liaison N≡N. The O-H and N≡N liaisons represent respectively 460kJ/mol and 941kJ/mol.
Because of all the energy that has been generated by the reaction, the water changes of phase and becomes gaseous. The propulsion of the space shuttle is not only the result of the energy but comes from the expansion of the gas: from one mole of gas we make 3 moles of gas. The gas expand very quickly because of the heat (pV=nRT), generating the explosion in the propeller.
Chapter 3 : thermodynamics – second and third principles
Second principle
Increase of the entropy: The entropy in the universe increases over time.
The entropy is a measure of the disorder of a system. The second law of thermodynamics has several formulations but the most common is that a process is spontaneous if, without external influence (isolated system), it induces an increase of the entropy in the universe.
For instance, if two reservoirs are connected, one being empty and the other one full of gas, the gas will spontaneously occupy the whole system even if it does not involve any variation of energy.
The gas dilates because there are more positions to occupy in a larger volume. Another definition of the entropy is that a system tends to change to the most probable state.
Imagine a small box with only a few available positions. Two particles are in this box and each one occupies one spot. Several combinations are possible:
If we increase the volume of the box, the amount of possibilities increases exponentially. It is an entropy of position/disposition. The formula of this kind of entropy for one particle is
Ω being the amount of possible configurations for this particle.
If the volume containing this particle changes from a volume V1 to a volume V2, the variation of entropy is
The number of positions for one particle is directly proportional to the volume and
For diluted gases, the volume of the particles is negligible with regard to the volume of the system. As a result, we can barely ignore the presence of other particles in the formula and say that for NA particles (1 mole)
We have seen earlier the dilatation of a gas that the energy was a state function but that the work and the heat were not and thus that the way the process takes place has an influence on the work and on the heat. The third path we discussed was the isothermal process for which we found an expression for the work
This process is isothermal so ΔE=q+W=0.
We can thus find the variation of entropy for this process from the heat. If the gas dilates, heat enters the system (it is an endothermic process).
The variation of entropy is thus equivalent to the quantity of heat that the gas has to absorb to keep its temperature constant.
The states of the matter don’t have the same entropy. A gas has an entropy way larger than a liquid, itself a bit larger than the one of a solid. We can easily understand that using the repartition of particles in a small box.
In a (perfect) gas, the particles don’t have interactions between them. They can thus occupy any position of the volume without restriction. In a liquid, the particles interact together and stay grouped but the shape of the cluster is not fixed. The possibilities are thus more limited than for a gas. In a solid, the particles are fixed together in a given shape. The positions that a solid can take are thus more limited than the ones that a liquid can take and way more limited than for a gas.
Tables of standard entropies exist and give the entropy of molecules in a given state at 298K.
To resume, several cases can be distinguished. A process occurs if the production of entropy in the universe is positive. This production of entropy is composed of the variation of entropy in the system and in the environment. One of those components of the entropy can be negative if the other component is positive and larger in absolute value.
When a reaction produces a gas, the variation of entropy is positive. If this reaction is exothermic, heat is transmitted to the environment, meaning that its entropy increases. This reaction is thus spontaneous. If the reaction was endothermic, the variation of entropy of the environment would have been negative. The reaction could still be spontaneous if the production of entropy of the reaction is larger than the decrease of entropy in the environment.
Cycle of Carnot
Nicolas Léonard Sadi Carnot proposed a way to convert thermal energy into work. It is a thermodynamic cycle, i.e. a series of transformations of state leading back to the initial state, composed of two isothermal processes (no temperature variation) and two adiabatic processes (no heat exchange with the environment). All the processes are reversible and the cycle can thus be done in the opposite way, converting work into a difference of temperature.
The setup is made of one reservoir the volume of which can change and that can be in contact with two bodies of temperature T1 and T2, T1 being larger than T2.
First step: isothermal expansion of the gas at T1. The reservoir is in contact with the hot body at T1. Heat q1 is exchanged between the body and the reservoir of gas that expands without variation of temperature. There is thus a variation of entropy ΔS1=q1/T1.
Second step: adiabatic expansion of the gas. During this second step there is no exchange of heat but the gas continue to expand, doing work on the piston and cooling from T1 to T2. The body at T=T1 is not in contact with the reservoir anymore. As there is no exchange of heat, there is no variation of entropy.
Third step: isothermal compression of the gas at T2. The reservoir is now in contact with the second body, at T=T2, causing a transfer of heat q2 while a compression is applied by the piston, keeping the temperature constant. There is thus a variation of entropy ΔS2=q2/T2.
Fourth step: adiabatic compression of the gas. The body at T=T2 is not in contact anymore and there is no possible heat transfer. The gas continue to decrease in volume while its temperature changes from T=T2 to T=T1. At the end of this step, the system is back in the conditions (volume, temperature and pressure) of the initial state.
The cycle can be plotted in the pV phase diagram as shown below:
The efficiency R=W/q1 of the cycle of Carnot would be 100% if all the work W was transformed into heat q. The work here is the difference of heating q1-q2 because ΔE=0=q+W (isolated system, the bodies at T1 and T2 being in the system). As a result,
It is possible to show that the ratio q2/q1 is equal to the ratio T2/T1.
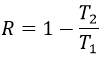
The consequence is that the efficiency is never at 100% except at T2=0K, that we can’t reach on earth. The loss of energy is caused by the production of entropy.
Free energy of Gibbs
For a reaction to occur, we just saw that two factors are important: the enthalpy of reaction (if the reaction is exo or endothermic) and the variation of entropy. The free energy of Gibbs ΔG regroups the two factors in one equation
A reaction is spontaneous if ΔG<0. The entropic term clearly shows that a reaction can be spontaneous at a given temperature but not if the temperature is modified
We can find tables for the values of the standard values of ΔH0 and ΔS0 and subsequently tables of ΔG0 for reactions of formations of molecules. At other temperatures but at 1atm, the relation is
Q is the reactive quotient that we already met previously
For instance, the reactive quotient of this reaction
Is
If ΔG is negative, the reaction goes towards the right, if it is positive, the reactions goes to the left. If ΔG=0, we are at the equilibrium. As a result, we can find a relation connecting the constant of equilibrium K with the free energy of Gibbs:
The chemical potential
The chemical potential μi is the energy of a molecule i that can be used during a reaction or a physical process.
Equation of Gibbs-Duheim:
The last term is thus a variation of energy in the system due to a variation of the quantities of particles in the system, something that we did not take into account before (it will be shown between brackets in the next equations). The relation above comes from the definitions of G and of H:
The partial derivatives of these functions are
We have seen that the internal energy ∂U=∂q+∂W-(∑iNi∂μi) and that ∂S=∂q/T and that ∂W=-p∂V. As a result
The chemical potential is thus the variation of free energy of Gibbs with regard to the variation of concentration of one specific species, keeping the other parameters (p, T and the concentrations of the other species) constant.
We also define the partial molar volume
that is useful for gases. From the law of perfect gases,
That leads us to the expression of the chemical potential for a gas
In solution, the formula is very similar
We know that
So we can find the expression of ΔG as a function of the pressures or of the concentrations of the species:
Yet, this is only true for ideal solutions and gases. Normally, we have to consider the activity a of each molecule
γ is equal to 1 for ideal solutions but may vary if the concentrations increases, representing the increase of interactions between species. However, the activity a of solids is equal to 1.
Third principle
The entropy of a perfect crystal at absolute zero is exactly equal to zero.
The third law provides a reference for the entropy of any pure crystal (and therefore to anything) at any temperature. A perfect and pure crystal is a crystal the arrangement of which is perfectly organised: there is no flaw, the matrix is regular and it is composed by one species. At the absolute zero, i.e. zero Kelvin, the state of the system is at the minimum possible energy. This state is unique as a result of quantum mechanics and it is indeed the case: there is only one way to place the atoms in a perfect crystal. The amount of possible configurations is thus 1, leading to an entropy equal to
If a base state is degenerated, i.e. there are several states of same energy, there are several different possible configurations Ω and the entropy is not equal to 0 but is very close to it. As soon as there is a flaw in the crystal, the amount of possible configurations increases. As a result, the entropy increases. This variation of entropy is synonymous to an variation of energy as told by the second law
The temperature rise dT due to the heat ∂Q is determined by the heat capacity (cp ≈ cV) of the crystal
Consequences of the third law
A first consequence of the third law is that T=0K cannot be reached by any number of finite processes. It is due to the fact that there is only one state of minimum energy. If we tried to change a given parameter in a controlled way so that the energy decreases each time, it would take an infinite number of repetition to reach the absolute zero. It is a bit similar to the problem of the bullet: If at each period of time a bullet moves from half of the necessary distance to reach its target, the target will be approached but never reached. If several states were allowed at T=0K, it would be possible to switch the parameter to obtain one or the other state: one value of the parameter approaches the system from one state and the other parameter approaches the system from the other state. With only one target, we cannot switch from one value of the parameter to the other and reach the final state. We can visualise this like this:
A second consequence is that the heat capacities cp and cV tend to zero when T tends to zero.