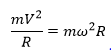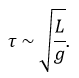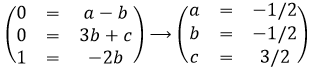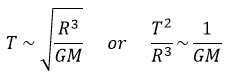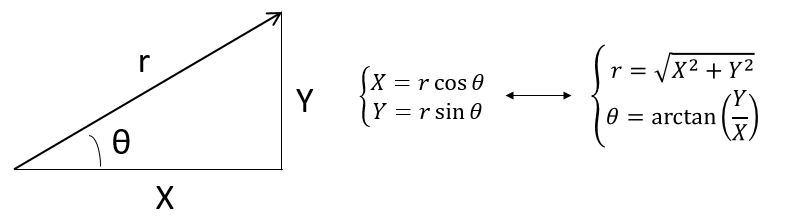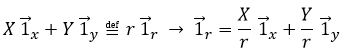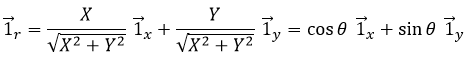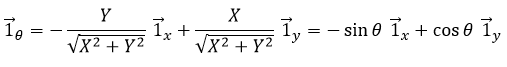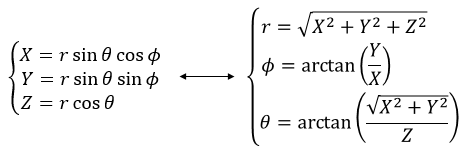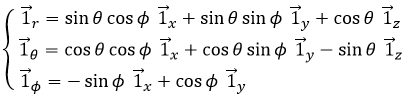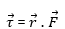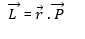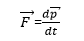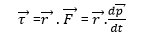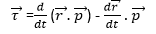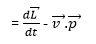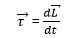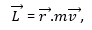Chapter 1: Elementary physics – Introduction
Definitions and laws
“One of the noblest desire of the man is to know the laws ruling the Universe, and those who contributed to enlighten some of the mysteries were always admired by their peers; they appear as privileged, wearing on them the divine light, a through centuries the generations gaze upon their indelible work and rank them first amongst the glories of the humanity.”
From Achille Cazin (Hachette, 1881).
Physics can be defined as a science that studies the general properties of matter, space, and time, and establishes laws that describe natural phenomena. We will point out the word law first, and ask ourselves if we can clearly, and without ambiguity, define all the objects we are discussing, i.e. space, time and matter. Their definitions are (Oxford dictionaries)
- Space: A continuous area or expanse which is free, available, or unoccupied.
- Matter: Physical substance in general, as distinct from mind and spirit; (in physics) that which occupies space and possesses rest mass, especially as distinct from energy.
- Time: The indefinite continued progress of existence and events in the past, present, and future regarded as a whole.
It is not what we can call clearly defined terms and it doesn’t indicate any of the relations that may exist between them. If we go back in time, Isaac Newton gave its definitions (1687):
- The absolute space, which is without any relation with anything from the surroundings, is always unchanging and immobile. The relative space is any measure or mobile dimension of this space, which is defined with regards to its position with regards to objects that we consider as the immobile space…
- The quantity of matter is the measure that we obtain from its density and its volume…
- The absolute time, true and mathematic, is without relation to anything from the surroundings, and by its nature flows uniformly. The relative time, is any measure, accurate or not, of the duration of an event, that we use in place of the true time. I.e. the hour, day, month,…
It is difficult to avoid cross references and circular definitions. We will abandon the idea to define everything and accept the fact that some notions can make sense without being explicit. Physics is seeking for the laws that rule the reciprocal actions between one object and its surrounding. Enouncing those laws is not an easy job, and we have seen many changes in the history, as the understanding of the scientists evolved. For instance, L. Wouters gives in a school book of 1916 the law for the dilatation of bodies due to heat as
“The first effect that heat produces on bodies is to increase their volume, to dilate them”
This law is based upon its hypothesis on the nature of heat:
“Based on the modern hypothesis on the nature of heat, it results from the vibratory movement of the smallest molecules of the ponderable matter, and is transmitted via a fluid called aether. Aether is a subtle, perfectly elastic, substance that fills the intermolecular spaces as well as the so-called interplanetary voids. Heat is, at the end, a particular state of movement.”
Today, it is obvious that this law is false, mostly because of the notion of aether it is based on. The law itself is true with some exceptions. So, shall we give no definition nor law? Obviously we will, but laws should results from the simple relations obtained from experimentations: if I modify one physical quantity of my experiment, then another physical quantity changes, at this effect is repeated consistently if I repeat the experiment.
To end this introduction, I will extend the citation of Achille Cazin (Hachette, 1881) I opened the introduction with.
“No matter the study on which we work, there are some general rules that one must follow to avoid falling in annoying confusions. …
In physics, we observe all the circumstances around a natural phenomenon; we measure all the available quantities; we seek relations between theses quantities, and these relations are called the law of the phenomenon. When the phenomenon is too complex, and it looks like it is impossible to state one unique law, we modify the phenomenon, we make an experiment. Some circumstances seeming ancillary, are made negligible, and we observe the dominating quantities. From this experiment we obtain an approximate law, and by extension we seek the influence of the neglected circumstances, in which way they alter the law. Doing that, we find the limit law towards which tends the observed law when the circumstances become more and more negligible. Such a law is then used as a fundamental principle, seen as the temporary expression of a physical truth, temporary because one more accurate observation or a new phenomenon can modify the conclusions admitted as truth until now.”
Chapter 1: uniform circular motion
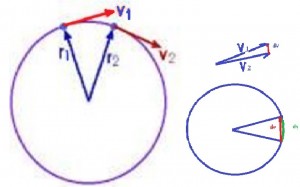
When an object has a circular motion even though its speed is constant, it is nonetheless accelerating because according to newton’s 1st law: an object continues in its state of rest or uniform motion unless acted on by an external force. So if the object was to be free in space then of course it will continue to travel tangentially in the direction that it has just before.
But if it changes the direction of the velocity ( the change of the velocity is acceleration). In fact,this acceleration is always towards the center of the circle and it’s called centripetal acceleration. And if we have an acceleration then the newton’s second law must be applicable which says: the force is equal to mass times acceleration (F= m.a ) then the centripetal force = mass X centripetal acceleration.
If the speed of objet is![]() and the radius of circle is R, then if the objet travels around one time, the distance that it travels is =2πR, it’s simply the circumference of the circle and imagine it does that in 60 seconds,so the velocity will be
and the radius of circle is R, then if the objet travels around one time, the distance that it travels is =2πR, it’s simply the circumference of the circle and imagine it does that in 60 seconds,so the velocity will be ![]() in m/sec.
in m/sec.
The another way of measuring is the angular speed and we know that the whole circle is 360°=2π. We use radians to measure angular speed, radians =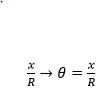
How many radians are there in a full circle? Full circle will be 2πR.
Angular speed: is designed by ω and ω=2π/t radians/second and we know that V= 2πR/t that means V= ωR, So this formula shows the relationship between the V (orbital velocity) and ω (angular velocity) .
Frequency (ƒ): is the number of cycles per second, we know that ω is the number of radians per second and we know that 2π is the number of radians per cycle then ƒ= ω/2π and we can write ω= 2πƒ.
Period (T), is the amount of time it takes to do one cycle And T= 1/ƒ so if ω=2πƒ then ω=2π/T
Centripetal acceleration:
Imagine the objet with a speed![]() at point a and after a short distance it will be at point b which will have an angle dθ (a very small angle).The distance travelled will be called dx (a small distance).
at point a and after a short distance it will be at point b which will have an angle dθ (a very small angle).The distance travelled will be called dx (a small distance).
The time of travelling = dt, so the objet travels a small distance (dx) sweeping out an angle called (dθ) and it does that in a short time (dt).
When it will be at b, the speed is still![]() because it doesn’t change the speed but it will be now in a different direction and if the speed changes that means the objet has been subjected to an acceleration.
because it doesn’t change the speed but it will be now in a different direction and if the speed changes that means the objet has been subjected to an acceleration.
Acceleration is the change of velocity during the time. To calculate the difference between two vectors we must put them tail to tail.what we are looking for is the streight line dy we know dθ= dy/v (small circle with r=v )
If dθ is very small, then the arc length y becomes the straight line dθ=dv/v
dx =Rdθ (=Rdv/v) dx= Vdt ⇒Rdv/v= vdt ⇒Rdv/dt= ![]() ⇒ dv/dt =
⇒ dv/dt =![]() = a
= a
Chapter 2: quantities and units
Units are necessary to evaluate quantities. Obviously, a rhinoceros is heavier than a dog, but to know by how much, we need some reference units. Moreover, rhinoceroses don’t all have the same weight. We are thus in need of a consistent unit to measure the weight of objects. The same problem appears for all the possible measures: we won’t measure with precision a distance with regards to the length of bananas because bananas don’t have a consistent length, and it is not convenient for many countries to use this unit of measure. Men have thus defined some quantities as references, quantities that are constant no matter the time or the external conditions (if not explicitly described). Note that some inaccurate units of measure are still in use in daily activities when accuracy is not that important. For instance, when cooking, we add x spoons of oil without giving explicitly the required weight or volume.
On the other hand, we can measure a distance in meters or in miles, the weight in grams or in pounds. All these units have a well-defined value and can serve as reference units. While some countries as the UK or the USA use some different units, international conventions defined an international system of units (SI base units). Their biggest advantage is the simple relation between the units of different quantities. In SI, one millilitre of water occupies one cubic centimetre, weighs one gram, and requires one calorie of energy to heat up by one degree centigrade, which is one percent of the difference between its freezing point and its boiling point. In the American system, you will need to make huge calculations to calculate how much energy it takes to boil a room-temperature gallon of water because you can’t directly relate any of those quantities.
The International Bureau of Weights and Measures (French: Bureau international des poids et mesures) is an intergovernmental organization, established to maintain the International System of Units (SI) under the terms of the Metre Convention (Convention du Mètre, May 20th 1875). The organisation is usually referred to by its French initialism, BIPM. Its role is to
- establish fundamental standards and scales for the measure of main physical quantities and to conserve the international prototypes;
- compare international standards with national standards;
- ensure the coordination of the corresponding techniques of measurement;
- measure and coordinate the measures of the fundamental, physical constants involved in the above activities.
SI Units
The definitions of the reference units are mainly made to give them a well-known and fixed value.
These definitions fix the speed of light c at 299792458 m/s et the permeability of the void μ0 at 4π 10-7 H/m exactly. They also sometimes require some precisions. For instance, we point out that the cesium atom is at rest, that the carbon atoms are not connected, are at rest and in their fundamental state.
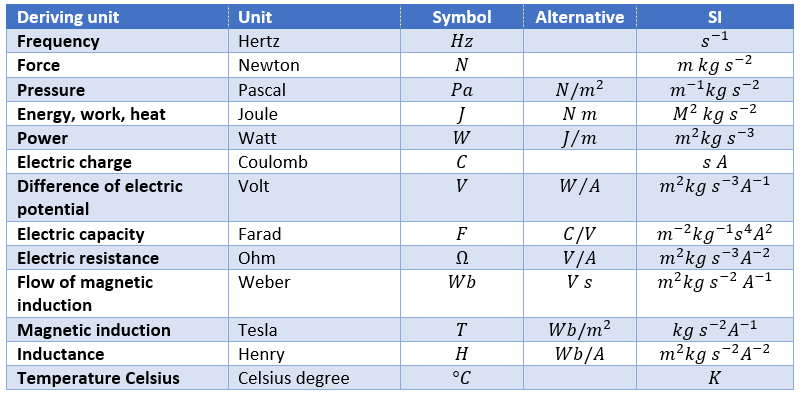
Deriving units
By commodity, some units are the combination of the SI units to express frequently used units.
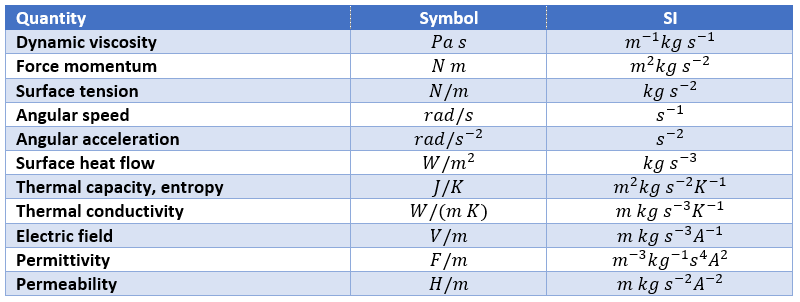
Finally, there are some quantities without specific unit names
We can point out a few specific units:
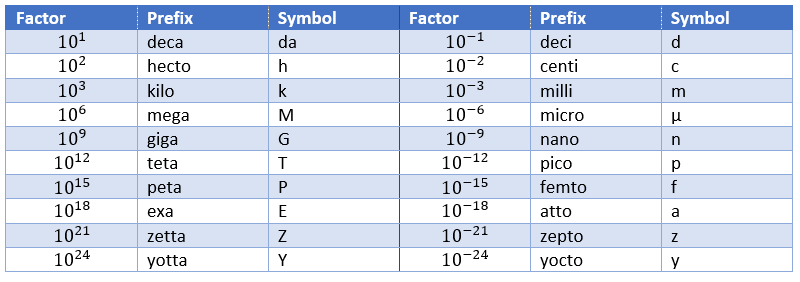
To put an end to this section, we will list the prefix of multiples of the SI units.
Dimensional analysis
The existence of the IS system means that all the other physical quantities have units that are homogeneous functions of these base units. A function is homogeneous if, making a scale change on all of its variables: x1 → λ1x1, x2 → λ2x2, x3 → λ3x3, … the function itself changes of scale: f(λ1x1, λ2x2, λ3x3,…) = λ1α1 λ2α2 λ3α3…f(x1, x2, x3,…). The units of any quantity, let’s call it Qr is thus always expressed by a relation like
So if we know the units of one physical quantity, and admitting that there is a relation between this quantity and other variables, and knowing the units of those variables, we can guess the relation between the quantities.
For instance, we observe the swinging of one object attached to one string: a pendulum. The pendulum oscillates because it falls and it is restrained by the string. We want to determine the relation between the times the pendulum takes to make one oscillation, i.e. the period, to the parameters we guess as important: the mass M of the object, the length L of the string, and the gravity acceleration g that affects each object on the planet. The units of the variables are kg for the mass, m for the length, and m/s² for the acceleration. The period is a time and thus its unit is s. The relation between the variables and the period should be something like this:
As there is no kg at the left of the equality, and it is present at the right side of the equation with the exponent a, then we conclude that a=0. Looking at the seconds, their exponent is 1 at the left and -2b at the right, b is thus b=-1/2. Finally, there is no m at the left while it is present at the right side of the equation, thus 0=b+c. As we determined the value of b, we have that c=1/2 and that the global relation is
From our dimensional analysis, we determined that the mass of the object has no influence on the period of the oscillation of the pendulum. Note that we did not write the equal sign: the dimensional analysis doesn’t give the true law; it gives clues on the variables but there can still be numerical factors that can be determined experimentally. On the other hand, the dimensional analysis allows to identify wrong laws not respecting the units of the quantities.
Let’s analyse a second example: the period T of revolution of planets around the Sun. First we identify the important parameters involved in the problem: the mass M of the Sun, the distance R between the planet and the Sun, and a constant G giving the gravitational force. The units of the parameters are respectively kg, m and kg-1m3s-2. The period is given in seconds s. The law should be of the form T ~ MaGbRc. For the units, we have the relation
The next step is to identify the exponent of each unit at the left and the right side of the equation:
The law is thus written
This relation is the expression of the Kepler’s law that describes the trajectory of planets of the solar system.
Scales and orders of magnitude
An experimental approach is to estimate the order of magnitude of variables that appear in physical processes. Either we measure the characteristics of one well known property of the matter, or we determine a transition zone between two models of description.
For instance, we can regroup the matter as solids, liquids and gases. One major difference between these three phases is their density, i.e. the mass of the matter for a given volume, given in kg/m3. We can thus regroup liquids as matter with a density with the order of magnitude around 103kg/m3 (at T=293K, water: 1003kg/m3, olive oil: 910kg/m3, sulfuric acid: 1834kg/m3,…)while gases have a density of order 1 (at T=273K, air: 1.2kg/m3, CO2: 1.98kg/m3, methane: 0.72kg/m3,…). Between solids and liquids, there is a factor 10 in density (at T=293K: iron: 7893kg/m3, copper: 8954kg/m3, gold: 19320kg/m3,…). We will want to determine the temperature at which a solid becomes liquid, i.e. its melting temperature.
As the interactions between particles of a solid differ from the interactions between particles in a gas, laws are not the same at the microscopic scale than in the astronomic scale, not because the interactions mysteriously disappear, but because we can neglect some interactions. For instance, imagine an interaction between particles that depends directly on the distance between two particles and one interaction that depends on the third power of the distance. If the distance is small, both interactions will have an effect, but as soon as the distance gets large, we can neglect the first interaction.
Chapter 3a: the motion- the position
The first formalism that has to be known in physics is the formalism of the motion. A formalism is associated with a certain rigorous mathematical method, defining symbols and rules that are commonly accepted, in the goal that everybody understands immediately the discussed matter. We will not be interested in the prediction of the motion nor its cause, but in its description alone.
In this section, we consider that every object can be considered as a dot without volume.
The position
The motionis the history of the position of an object, the succession of the positions of this object over the time. To define the position of the object, we need a reference system in which we can give the position: coordinates. Several systems of reference exist and there are several ways to calculate the coordinates of objects. All of them are corrects but some are more convenient than the others. During a trip, you won’t give your position with regard to the sun, the same is true in physics.
Several coordinates are generally necessary to determine the exact position of one object. If you say that you are 10km from Paris, you give an information on your position but we are lacking at least one coordinate to determine your position. Usually you need one coordinate by dimension of the system.
One dimension
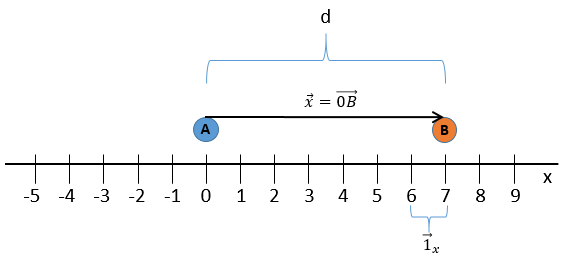
We choose one origin to the coordinate system, the zero point. It is convenient to choose the initial position of the object A as the origin but it is not mandatory. Next we choose a direction that will be the positive positions. In the opposite direction we have the negative positions. Still for convenience, the positive positions are placed in the direction we guess the object will move towards. Imagine that the object moves towards another object B placed at a distance d. The position vector indicates the distance between an object and the origin, and points towards the object with an arrow. The symbol for vectors is topped by an arrow pointing to the right. The position vector for B is
Where ![]() is the unit vector in the direction x (the single direction in this problem).
is the unit vector in the direction x (the single direction in this problem).
Two dimensions
The second coordinate is usually orthogonal, perpendicular to the first coordinate to avoid a maximum of angle problems and to benefit the simplicity of the calculation for right triangles. Each coordinate has a direction.
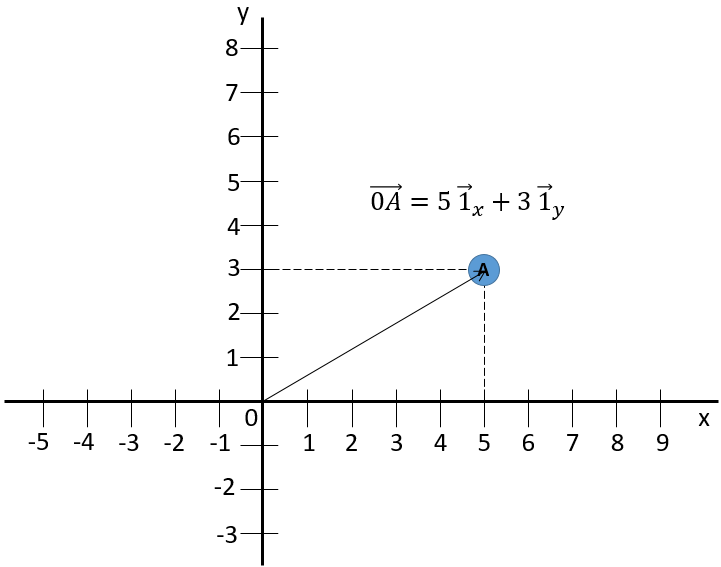
The position vector is now defined by two components from which we can calculate its length if desired.
The addition sign between the two unit vectors is seen as “followed by” and not like the addition of two usual numbers. Another way to write coordinates is to put them in brackets. If we do this, then we don’t write the unit vectors.
This system of reference, the Cartesian system, is not the single one that can be used at two dimensions to determine the position of an object. We can also position the object from its distance r to the origin point and an angle θ from one axis. This reference system is called the polar system.
It is possible to determine the relation between the coordinates X;Y in the Cartesian system and r;θ in the polar system using the relation defining the cosine, the sinus and the tangent:
The unity vector ![]() can thus be calculated.
can thus be calculated.
or
We can also define the unit vector ![]() :
:
Both polar unity vectors depend thus upon θ that should thus be chosen conscientiously.
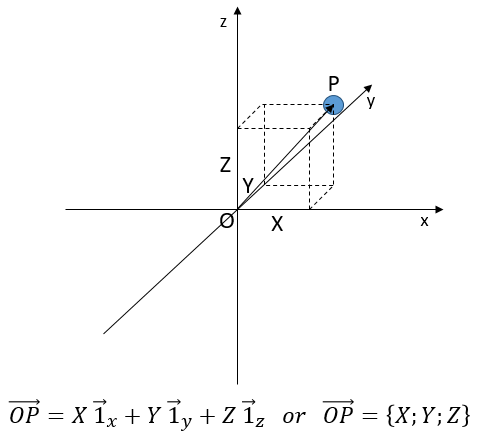
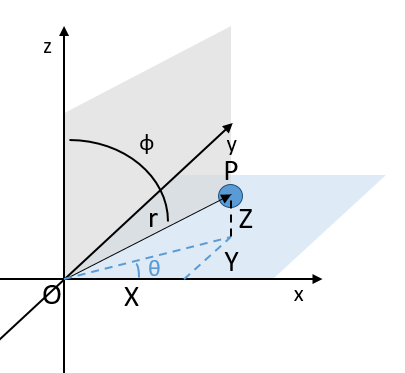
Three dimensions
A third coordinate is added in the reference systems. In the Cartesian system, we add a coordinate that is orthogonal to the two previous ones.
In the polar system, we need a second angle to determine the position of an object. We take the first from the axis x in the xy plane and the second angle is taken from the z axis in the zr plane of the object.
Again, the Cartesian system can be associated to the polar system.
The unit vectors are defined as
Chapter2: torque and angular momentum in circular motion
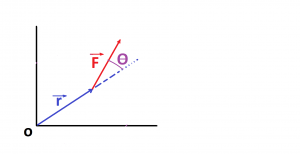
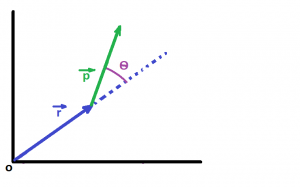
Definitions: the torque and angular momentum are defined as vector products of position, force and momentum. Suppose a force![]() acts on a particle whose position with respect to the origin 0 is the displacement vector
acts on a particle whose position with respect to the origin 0 is the displacement vector ![]() . Then the torque “about the point 0 and acting on the particle,” is defined as:
. Then the torque “about the point 0 and acting on the particle,” is defined as:
Now suppose the particle has a liner momentum P relative to the origin. Then the angular momentum of the particle is defined as:
The direction of ![]() and
and ![]() are given by the right-hand rule for cross products.
are given by the right-hand rule for cross products.
Relationship: = Using the definitions of torque and angular momentum, we can derive a useful relationship between them.
Starting from Newton’s second law, written in the form:
The torque is:
This can be rewritten using the expression for the derivative of a cross product:
Now![]() so
so ![]() (because the vector product of parallel vectors is zero), so the torque is:
(because the vector product of parallel vectors is zero), so the torque is:
Thus the time rate of change of the angular momentum of a particle is equal to the torque acting on it.
Motion confined to a plane:
The expression ![]() for a particle takes on a scalar appearance when the motion of the particle is confined to a plane.
for a particle takes on a scalar appearance when the motion of the particle is confined to a plane.
Consider a particle constrained to move only in the x-y plane, as shown in Fig.2. the torque on the particle is always perpendicular to this plane as is the angular momentum .
Equivalently, we say that![]() and
and![]() have only z-components. Since their directions remain constant, only their magnitudes change. Then:
have only z-components. Since their directions remain constant, only their magnitudes change. Then:
This equation holds only if ![]() are in the same plane; if not (and they won’t be for non-planar motion), the full Eq. must be used.
are in the same plane; if not (and they won’t be for non-planar motion), the full Eq. must be used.
Circular motion of a Mass: The torque and angular momentum for the special case of a single particle in circular motion can be easily related to the particle’s angular variables. Supposed a particle of mass m moves about a circle of radius r with speed v (not necessarily constant) as shown in Fig.3. The particle’s angular momentum is:
But since ![]() are perpendicular, the magnitude of L is:
are perpendicular, the magnitude of L is:
And the direction is out of the page. This equation may be rewritten in terms of the angular velocity (since ![]() ) as:
) as:
Similarly, the torque is:
Where α is the particle’s angular acceleration.
Systems of Particles
Total Angular Momentum: The total angular momentum of a system of particles is simply the sum of the angular momenta of the individual particles, added vectorially. Let ![]() be the respective angular momenta, about a given point, of the particles in the system. The total angular momentum about the point is:
be the respective angular momenta, about a given point, of the particles in the system. The total angular momentum about the point is:
As time passes, the total angular momentum may change. Its rate of change ![]() , will be the sum of the rates
, will be the sum of the rates ![]() for the particles in the system. Thus
for the particles in the system. Thus ![]() will equal the sum of the torques acting on the particles.
will equal the sum of the torques acting on the particles.
Total Torque: The total torque on a system of particles is just the sum of the external torques acting on the system. The torque due to internal forces is zero because by Newton’s third law the forces between any two particles are equal and opposite and directed along the line connecting them. The net torque due to each such action-reaction force pair is zero so the total internal torque must also be zero. Then the total torque on the system is just equal to the sum of the external torques:
For the system, then:
In words, the time rate of change of the total angular momentum about a given point, for a system of particles, is equal to the sum of the external torques about that point and acting on the system.
Rigid Body Motion About a Fixed Axis: A rigid body is a system of particles whose positions are all fixed relative to each other. Since ![]() for each particle in the body, we may write for the total angular momentum:
for each particle in the body, we may write for the total angular momentum:
Where we have assumed that the body is rotating about a fixed axis with angular velocity : ![]()
And, since the axis of rotation is fixed, equations with a scalar appearance hold for the torque: