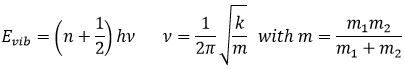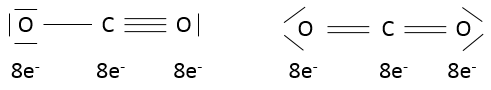Atoms make liaisons because they get more stability. A proof is that to break a liaison, we need to give energy to the molecule.

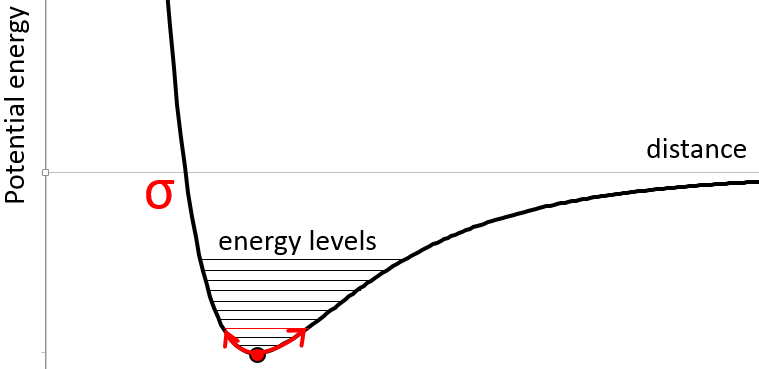
Atoms in a molecule are at a given distance, and oscillate slightly from this position depending on the energy they receive.

The atoms cannot oscillate at any frequency. There are authorized levels of energy at which the atom can be placed.

Even at n=0, the fundamental state, the atoms oscillates at a given frequency.

It is difficult to approach more the atoms from each other but it also requires energy to pull them away. The dissociation energy is the energy required to separate two atoms by an “infinite” distance.

To form a liaison, the clouds of electrons around the nuclei concentrate between the two nuclei to shield their charge and decrease the repulsion between them. The repartition of electrons differs depending on the type of liaison. New orbitals, molecular orbitals are formed from the atomic orbitals to bind two atoms.

Only the last layer of electrons, the electrons of valence, is taken in account for the molecular orbitals: the inner layers are too distant to interact.

4 types of liaisons exist: covalent, ionic, metallic and coordinative liaisons (or hydrogen bridges). We will develop the two first types of liaison here

Covalent liaisons:

Such a liaison is made between atoms of same electronegativity (or almost). Each atom put one electron in common to make a covalent liaison. The electrons in the liaison are shared equally along the liaison.

Ionic liaisons:

Such a liaison is made between atoms of different electronegativity. In an ionic liaison, the electrons are not shared equally. One atom is the donor of electrons and the other is the acceptor of electrons. The acceptor is more electronegative than the donor.

As the electrons are not equally shared, a gradient of charge exists along the liaison. We say that there is a dipolar moment.

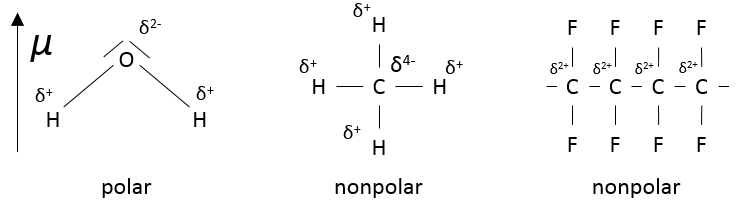
Polarity

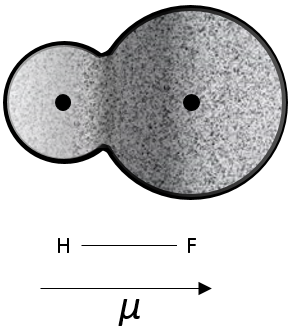
H and F have different electronegativities (2.1 and 4 respectively). Most of the electrons of the liaison are thus closer to the atom of fluorine than to the atom of hydrogen.

The dipolar moment μ of this liaison can be defined as

By definition, the dipolar moment goes from the positive charge to the negative one. If the charges were completely separated, this moment should be

D stands for Debye and equals 3.336Cm.

The value obtained experimentally is 1.83D. It means that the hydrogen does not totally give its electron to the fluorine. The ionic character of a liaison is given by

And if this value is over 50%, we consider that the liaison is an ionic liaison.

Fluorine has the highest electronegativity but has not a polarity large enough to have an ionic bond with the hydrogen (only 41.6%). The reason is that both H and F have a very small radius and that the liaison’s length is thus small and the liaison is strong. It is the reason why HF is a weak acid while the other acids of halogen are strong acids: the negative charge is more stabilised on Cl^–, Br^– and I^– than on F^–.

Note that a molecule that has polar bonds is not automatically polar CH₄ is nonpolar. The polyfluorocarbon (CF₂)_n is nonpolar as well.

Polar molecules are soluble in polar solvents and nonpolar molecules are soluble in nonpolar solvents. In polar solvents, the acceptor and the donnor of electrons dissociate because the charges of the ions are stabilised by the solvent molecules (the solvation has been explained in the section on the nucleophile substitutions). For instance, when we put some NaCl into water, the salt dissociates into the ions Na⁺ and Cl^–. If this salt is put in a nonpolar solvent, NaCl remains as one molecule.

On jackets, nonpolar molecules are grafted so that rain does not penetrate the jacket but can only roll on it. On a nonpolar surface, water does not spread but restricts its surface at the maximum, forming a sphere.

Rule of the octet and formal charge

Through bonding, atoms try to have 8 electrons of valence, the electronic configuration of noble gases. For example CaCl is not a correct molecule. Ca has 2 electrons of valence and Cl has 7. To bind, Ca gives one electron to Cl. Cl reaches the octet but Ca has still one electron of valence to lose. The correct formula is CaCl₂: Ca gives one electron to two Cl to reach the electronic structure of the noble gas Argon.

In CO₂, the liaisons are covalent and the electrons are shared between C and O. CO₂ could possibly have two structures:

One can see that the oxygen’s of the molecule of the left are not equivalent. In a molecule, the electronic distribution has to be the most homogeneous possible. Each atom has a formal charge (FC)

 

Let’s check the FC of each atom:

 

In the molecule of the right, atoms don’t have formal charges and this molecule is thus more stable than the molecule of the left, where charges are separated. In fact, the first molecule is a resonance form (i.e. a structure with the same composition but a different electronic repartition), but less stable, of the second molecule:

The rule of the octet works very well for the three first lines of the Mendeleev table. After that, some empty nd orbitals can be used to bind atoms. For example S can bind 6 atoms of fluor (SF₆).

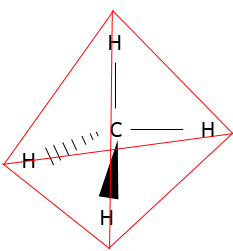
Now, is that molecule really linear, as we draw it? To determine the spatial structure of a molecule, we have to consider the atomic orbitals of each atom and the fact that liaisons are repulsive between each other (they are densely negatively charged). CO₂ is thus linear, having an angle of 180° between the two double liaisons to reduce the repulsion between them. CH4 is a regular tetrahedral, having an angle of 109° between each liaison:

The black triangle is a liaison going in the direction of the reader and the dashes represent a liaison goind in the opposite direction.

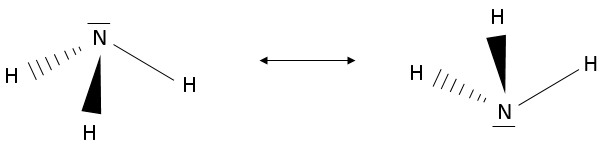
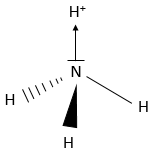
The lone pairs also take space in a molecule. In fact, they take more space than a normal liaison: the electrons are piled up near the atom. As a result, H₂O is not linear but is a tetrahedral. Yet, it is not a regular tetrahedron as the angle between the lone pairs (>109°) is greater than the distance between the liaisons (<109°). NH₃ is tetrahedral as well but has the specific particularity that it quickly oscillates between two equivalent forms:

Hybridisation

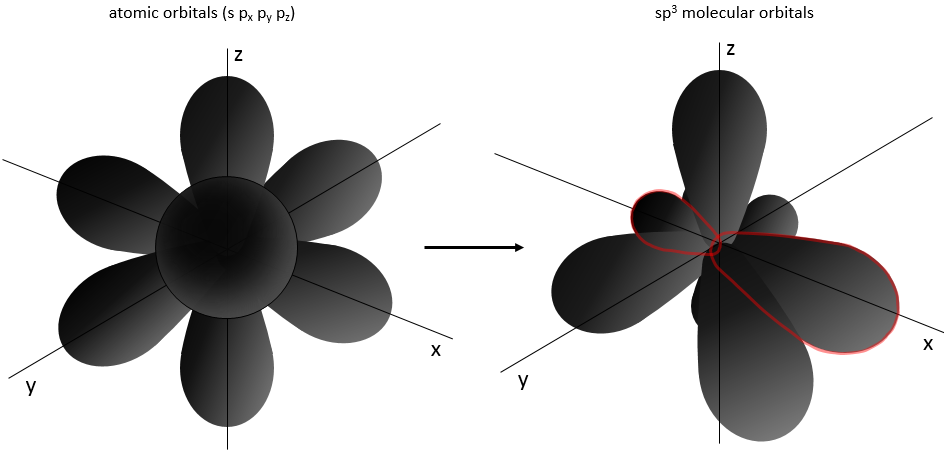
We have seen earlier the forms of atomic orbitals (AO) and none of them was tetrahedral. The atomic orbitals mix together to form new molecular orbitals (MO) that are used to bind with other atoms. It is the hybridisation process.

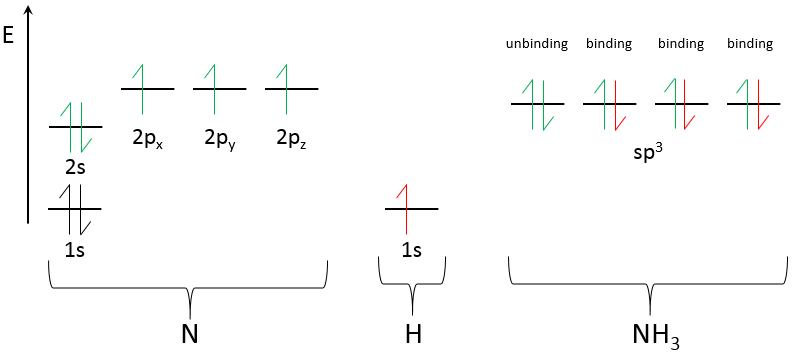
One of the molecular orbitals is outlined in red for convenience. These hybrid orbitals are the result of the hybridisation of the atomic orbitals s and p. The orbitals ns and np have different energies and merge into molecular orbitals sp of equal energies. Only the last layer of orbitals (with exceptions) merge to form a new set of orbitals. The inner orbitals are not modified as shown for NH₃ next:

N has 5 electrons of valence: 2 in 2s and 3 in 2p. They merge into 4 sp³ orbitals of equal energy. The exponent 3 on the p indicates that 3 orbitals p were merged with one (not indicated as an exponent) orbital s. As usual, the electrons are placed on all the orbitals before being paired. One orbital contains 2 paired electrons already: it is the lone pair. The three other sp³ orbitals contains 1 electron each. The hydrogen will bring one additional electron on those orbitals to bind and form NH₃.

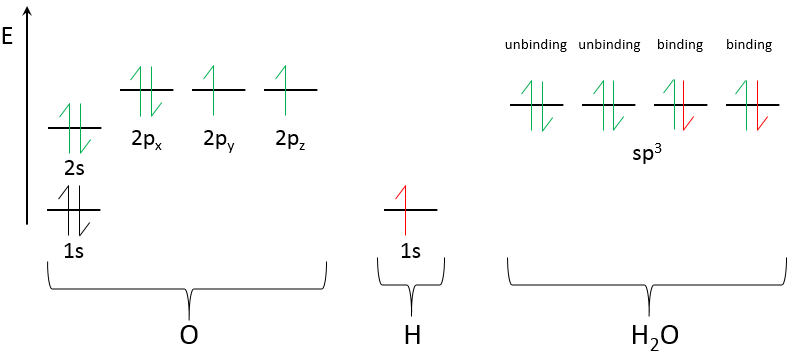
We can do the same for H₂O:

The oxygen has one more electron than the nitrogen. It results in a second lone pair and only 2 hydrogen’s binding to O.

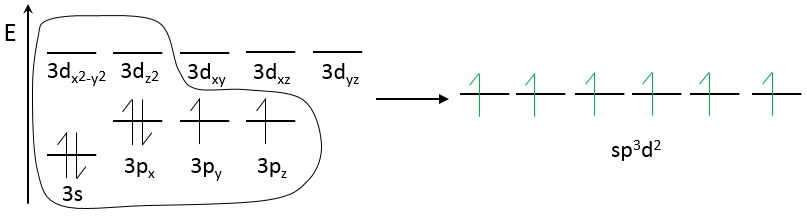
For SF₆, two empty 3d orbitals are used.

Four of the six liaisons are in the same plane and the two others are on each side of this plane. SF₆ has thus a octahedral structure.

Bonding and antibonding orbitals

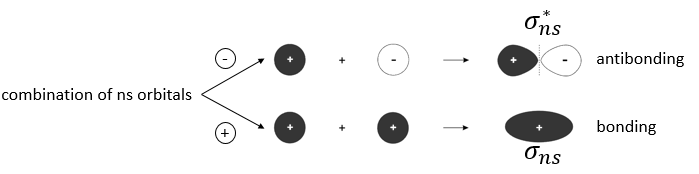
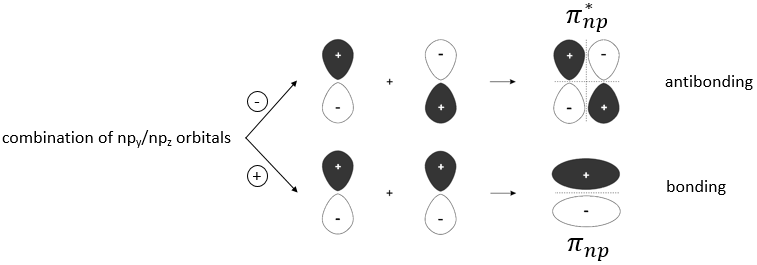
When two atoms are approaching each other, their outermost atomic orbitals interact to form molecular orbitals. We have seen earlier bonding orbitals but it is not the only possible combination of orbitals that can take place. The combination can either be positive or negative.

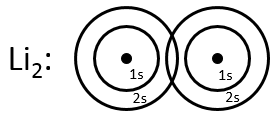
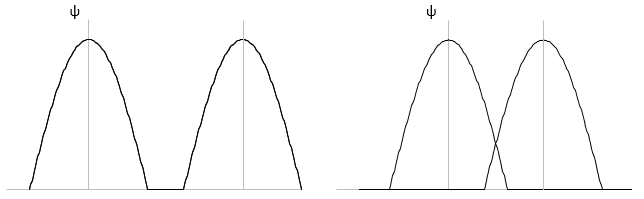
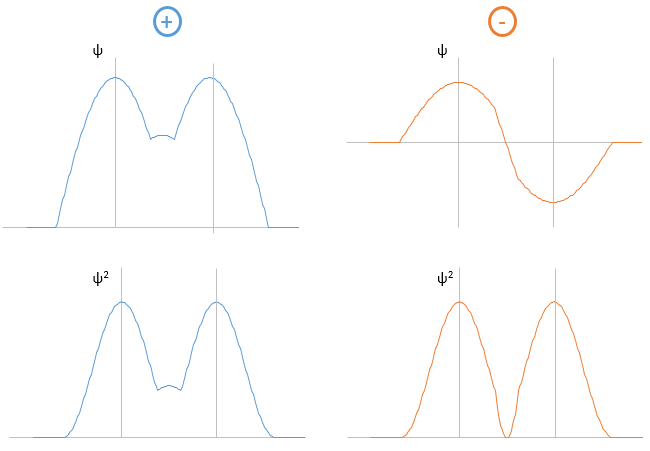
Li₂ combines the 2s orbitals of each atom. The positive and negative combinations of the wave functions give

If we put this to the square, we obtain the probability of presence of the electrons. In the case of the negative combination, one can see that between the atoms, there is a point where the probability of finding electrons in null. It leads to an antibonding orbital. In the case of the positive combination, the probability of finding electrons between the atoms is high everywhere. It leads to a bonding orbital. Bonding orbitals are stable and lead to a persistent liaison. Antibonding orbitals are unstable and liaisons are not made. We denote those orbitals with a *. The molecular orbitals resulting from ns orbitals are called sigma σ:

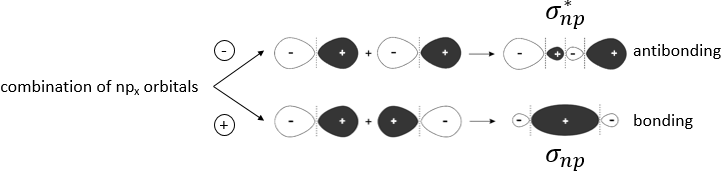
The same kind of bonding and antibonding orbitals exist for the np, nd and nf orbitals. The np orbitals in the direction of the liaison form a sigma orbital and the other np orbitals are responsible for the double and triple liaisons and are called liaisons pi.

The molecular orbitals have different energies and we will now explain how to determine which orbitals are used and which ones are not.

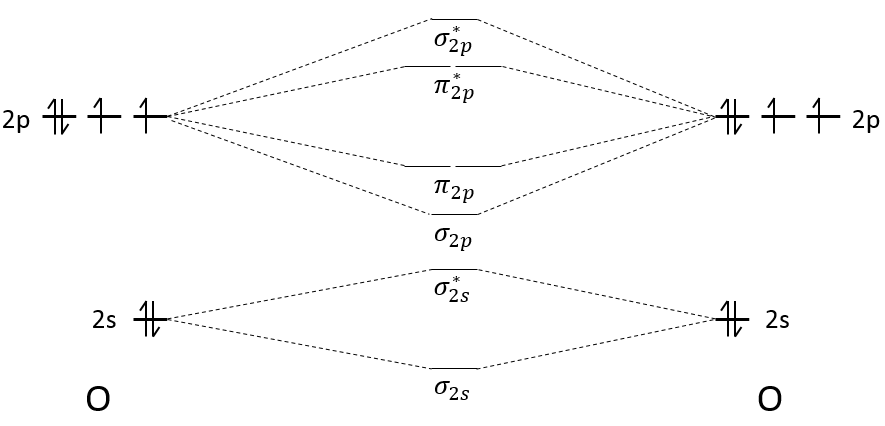
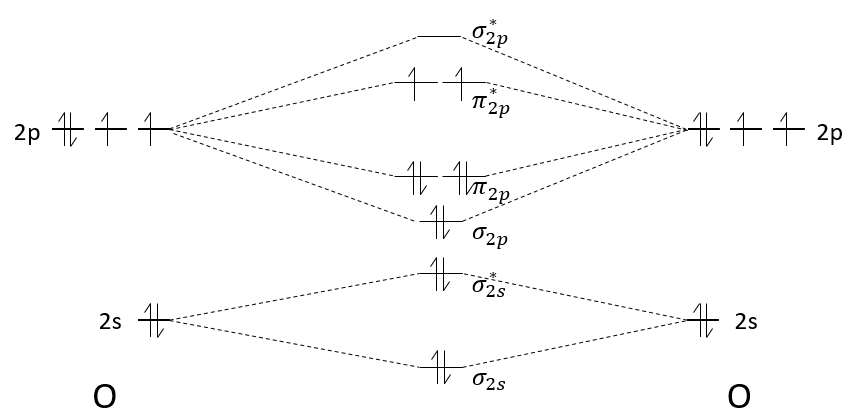
The atomic orbitals of the two atoms are placed on the left and on the right. On the middle, we place the molecular orbitals that result from the atomic orbitals.

Each orbital gives one bonding and one antibonding molecular orbital. The molecular orbitals are placed from bottom to top, going from the less energetic to the most energetic orbital. For Z<8, the MO π_2p and σ_2p are inverted: the MO σ*_1s and σ_2s are repulsing each other. To determine the energy of a molecular orbital, we use the linear combination of atomic orbitals (LCAO) method. This method will not be explained right now, but probably in the second or third year lessons. Yet, as it is a linear combination, the average energy of the molecular orbital obtained from atomic orbitals equals the average energy of those atomic orbitals. For example, the energy of the molecular orbitals σ_2s+ σ*_2s equals the energy of the atomic orbitals 2s+2s. It is also the case when the atomic orbitals don’t have the same energy.

The second step is to distribute the electrons on the MO. The electrons are distributed from bottom to top and each molecular orbital accepts 2 paired electrons.

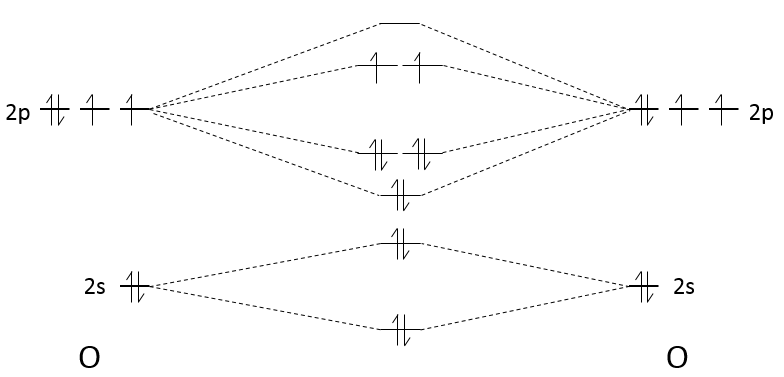
The effect of building those molecular orbitals is that the energy of the electrons has been decreased: only 2 electrons have a higher energy than the 2p orbitals but 6 have a smaller one (not counting the electrons from the 2s orbitals). The order of the liaison gives a good idea of the strength of the liaison and is given by:

The order tells us that the liaison between two oxygen’s is a double liaison. When the order of liaison is great, it means that the liaison is energetic and short.

Magnetism

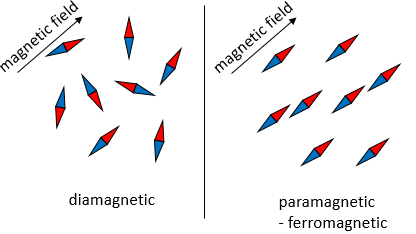
Magnetism is the reaction of a particle to a magnetic field. As a reaction to a magnetic field, a particle orientates against the magnetic field or in its direction. This behaviour depends mainly on the electronic structure of the particle and on the temperature.

Diamagnetism

Diamagnetism is the opposition of any particle to a magnetic field. It appears in all materials but is very weak with regards to other magnetic behaviours. As a result, it is only observable in purely diamagnetic materials. To be so, a diamagnetic material has all its electrons paired. The opposite spins of paired electrons cancel the intrinsic electron magnetic moment: electrons are charged species revolving in one direction (spin) around the nucleus and can interact with an external magnetic field.

Paramagnetism

Unpaired electrons line up with a magnetic field and orientate particles in the same direction that the magnetic field. However, when the external field is removed, the particles do not retain the magnetic properties.

Ferromagnetism

It is the strongest reaction to a magnetic field and is the property of magnets. As for paramagnetism, unpaired electrons line up with a magnetic field but an additional effect exists for ferromagnetic particles: the aligned, adjacent particles exhibit a magnetic dipole-dipole interaction. Under certain conditions, the orbitals of their unpaired electrons can overlap. As a result, a similar effect than the exclusion of Pauli applies: it reduces the electrostatic energy of the electrons when their spins are parallel and not anti-parallel. The difference of energy between the parallel state and the anti-parallel state is called the exchange energy and defines the strength of the ferromagnetism of a particle.

Colour

The colour of compounds comes directly from the difference of energy between the highest occupied molecular orbital (=HOMO) and the one above it (=LUMO, lowest unoccupied molecular orbital). The molecule absorbs light to excite one electron. To jump by one level, the photon must have the same energy that the difference of energy between the levels. It means that only the light of a given colour is absorbed. Because this colour is absorbed, we don’t see it but see the colours that are not absorbed by the molecule.

Fluorescence is the light emitted when an excited electron de-excites to an intermediate level instead of its fundamental level. The emitted colour is thus different than the one absorbed and the process is very slow.

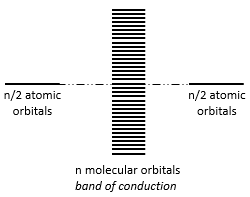
Metallic liaisons

In a metal, all the atoms are bound together. The molecular orbitals merge into a continuum band of conduction. As a result, the electrons are shared by all the atoms in the metal and electons can move along the metal. It is why metals conduct electricity.

Coordinative liaisons

Coordinative liaisons are liaisons made when an atom wearing one (or more) lone pair of electrons uses one pair to bind a cation.

The two electrons of a coordinative liaisons come both from one atom. The geometry of the molecule does not change when a coordinative liaison is made and the liaison has to be at the initial position of the lone pair.

In hydrogen bonds, the cation is a proton. These liaisons are weaker than a normal covalent liaison but can have an important role in the structure of a compound.

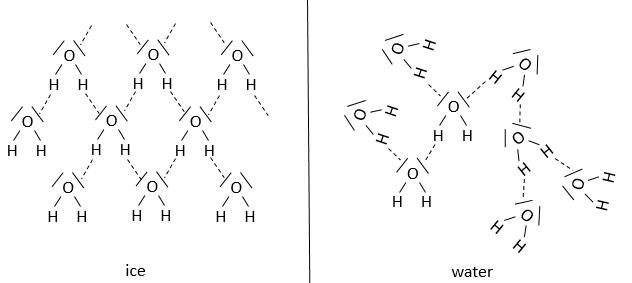
For example, the difference between ice and water is the proportion and the arrangement of the hydrogen bonds. Indeed, the hydrogen bonds are working in synergy to  strengthen the structure. There is a restriction for the angle between the hydrogen bond and the other liaison of the hydrogen, which depends on the compound. The presence and absence of hydrogen bonds have a big responsability in the structure, and thus the effectiveness, of proteins.

The cation can also be a metal of transition. In this case, the bonding molecule is called a ligand. The ligand will target the empty nd orbitals of the metal. The geometry of the resulting compound is tetrahedral or octahedral depending on the generated molecular orbitals.

The atomic orbitals nd splits into two levels of different energy. The lower energy orbitals are d_xy, d_xz and d_yz for the octahedral structure and the orbitals d_x2-y2 and d_z2 have a higher energy.

It is the opposite for the tetrahedral structures.

The chemistry of coordination is a complex domain of the chemistry and it will be discussed in details in the courses of second year.

Exercises

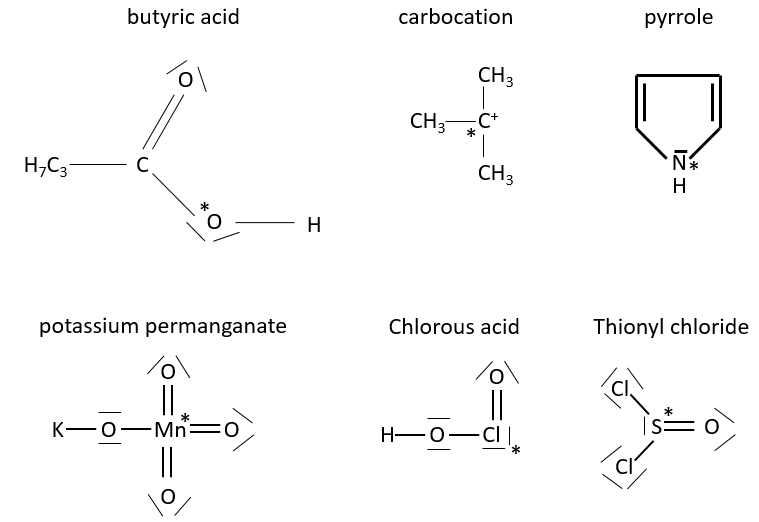
1.  What is the formal charge of the atoms with a *?

2.  Which of those diatomic molecules are paramagnetic and what is their order of liaison? O₂, N₂, C₂, F₂, B₂

3.  What is the spatial structure of these molecules?

CO₂, NO₂, H₂0, CH₃⁺, C₂H₆, BF₃, C₂H₂, HCN

4.  Explain why SiF₄ is nonpolar while the liaison Si-F is polar.

5.  Do these molecules have a dipolar moment? CCl₄, HCl, F₂, CO₂, H₂O, (C₂ClH₃)_n

6.  Why is the angle of liaison in SCl₂ equal to 101°?

7.  What is the hybridisation of the underlined atoms in these molecules? What is the spatial geometry around them?

H₂O, XeF₄, PCl₅

Answers

1.

Butyric acid: FC_O*=6-4-4/2=0

Carbocation: FC_C⁺_*=4-0-6/2=1

Pyrrole: FC_N*=5-2-6/2=0

Potassium permanganate: FC_Mn*=7-0-14/2=0

Chlorous acid: FC_Cl*=7-4-6/2=0

Thionyl chloride: FC_S*=6-2-8/2=0

2.  Let’s focus on O₂ and then extend the reasoning to the other species. Each oxygen atom has 6 electrons of valence. To determine if a molecule is paramagnetic, we need to know if there are unpaired electrons. To do so, we apply the LCAO (linear combination of atomic orbitals).

There are 2 unpaired electrons in the π*_2p orbital. O₂ is thus paramagnetic. The order of the liaison is given by

For the other species, we can do the same thing. Nitrogen has one valence electron less than the oxygen. The π*_2p orbitals are thus unoccupied and N₂ is not paramagnetic. The order is (8-2)/2=3.

C₂: paramagnetic, order: 2

B₂: not paramagnetic, order: 1

F₂: not paramagnetic, order: 1

3.  CO₂: linear

NO₂: linear

H₂0: bend

CH₃⁺: planar

C₂H₆: tetrahedral

BF₃: planar

C₂H₂: planar

HCN: linear

4.  The dipolar moments of the liaisons cancel each other.

5.  CCl₄: No

HCl: Yes

F₂: No

CO₂: No

H₂O: Yes

(C₂ClH₃)_n: Yes

6.  The S atom has 6 valence electrons, as the oxygen does. It means that S has a sp³ configuration with 2 liaisons and 2 lone pairs. The normal angle between liaisons for the sp³ configuration is 109.5° and there is a smaller angle in SCl₂ because lone pairs take more space than liaisons because electrons are packed nearby the atom.

7.  H₂O: sp³

XeF₄: sp³d²

PCl₅: sp³d