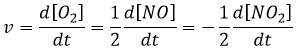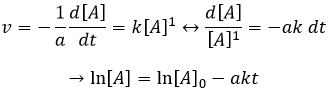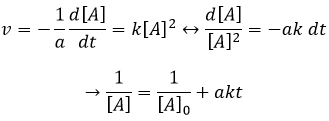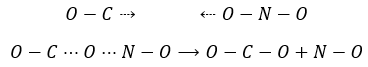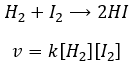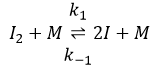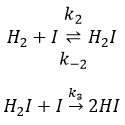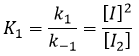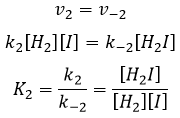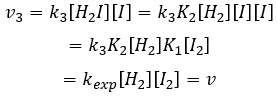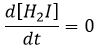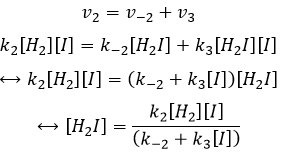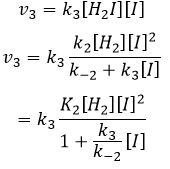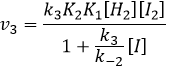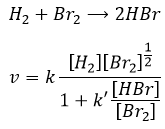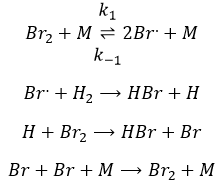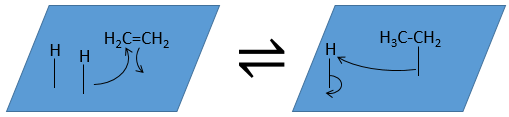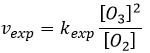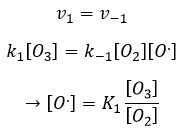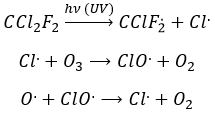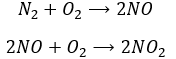Kinetics
Kinetics is a field of the chemistry that studies the speed of reactions. The speed of a reaction can depend on the conditions of the reaction. For instance, when we put H2(g) and O2(g) we don’t produce water spontaneously.
This reaction has a very negative ΔG0. However, if we produce a spark, the reaction will go very fast.
We have seen that the temperature has an influence on the equilibrium of reactions. At SCTP, the formation of ammonia has a negative ΔG0 but it becomes positive for temperatures larger than 434K.
Without temperature variation one reaction can be speeded up if we use a catalyst. We will discuss catalysts later in this chapter.
It can thus be important to know the speed of reactions in function of several parameters in order to optimise the production of one particular molecule, the destruction of some waste or any other process.
Speed of reaction
The speed of a reaction is the variation of concentration of the involved species in function of the time. It is always positive. As there can be several different stoichiometric coefficients, we have to agree on the definition of the speed of a reaction because the concentrations don’t vary the same way. To obtain this speed, we divide the variation of concentration over time of the corresponding species by the stoichiometric coefficient. In the reaction
we consider only one speed of reaction which is
The concentrations of reactants decrease over time and the speed is of the opposite sign than the variation of their concentration.
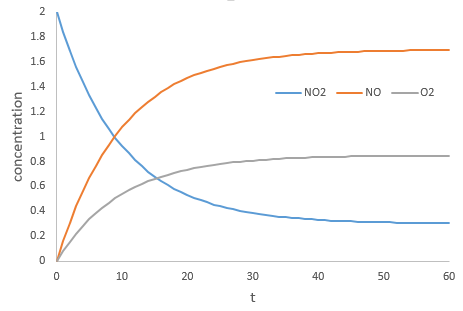
During the reaction, the speed depends on the concentrations of all the involved species.
The coefficients α, β and γ are the order of the reaction with regard to the corresponding species. α is the order of reaction with regard to NO2, β to NO and γ to O2. The order of the reaction with regard to one species is often their stoichiometric coefficient but not systematically. The sum α+β+γ is the global order of the reaction.
At the equilibrium the speed of the reaction in one direction is equal to the speed of the reaction in the other direction.
It is not true to say that v=0. The two reactions have the same speed.
At the beginning of the reaction, we can neglect the concentrations of the products in the expression of the speed with β=γ=0. The speed at the beginning of the reaction is thus simply
Integral method
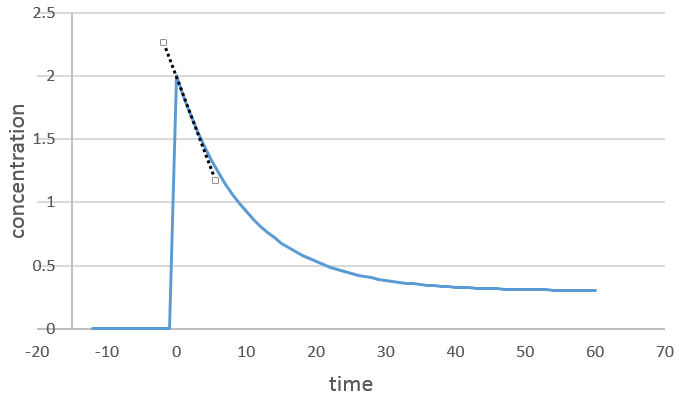
We can determine the order of the reaction with regard to one species by keeping constant the concentrations of the other reactants. Basically, we put a large excess of reactants except for the species that we want to study. This way, only one concentration varies significantly. During the reaction, we detect the variation of the concentration of the target species over time.
We focus on the period of time just after the beginning of the reaction. Before it, there is no variation to be detected (the reactant is probably not even in the solution) and later the products can play a role in the speed of reaction.
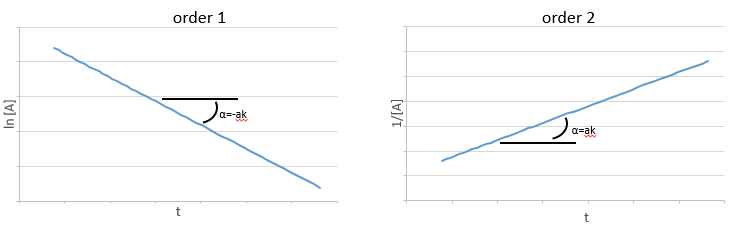
If the reaction is of order 1 with regard to the target species, the speed is
And thus we can find a straight line when we plot ln[A] in function of the time, the slope of which is –ak
If the order=2, the ln[A] won’t give a straight line but 1/[A] does. In this case, the slope is ak.
The order can also be equal to zero, meaning that the concentration of the reactant does not matter (except for very small concentrations). That means that the reaction is limited by something else. We often observe order zero reactions in presence of catalyst.
A catalyst is a species that affects the reaction but is not consumed during the reaction. The most common catalysts are solid but some catalysts are liquid. On solid catalysts, the reactants can bind on the catalyst. Because of this new liaison, the liaisons in the reactant are weaker and the reactivity is improved. The reaction is thus limited by the available surface on the catalyst. The solution is mixed during the reaction so that there is always reactants in the vicinity of the catalyst. Otherwise the reactants would be further and further of the catalyst as the time goes on. The evolution of the concentration would be more complex in this case. We will discuss furthermore about catalysts later.
Method of the initial speeds
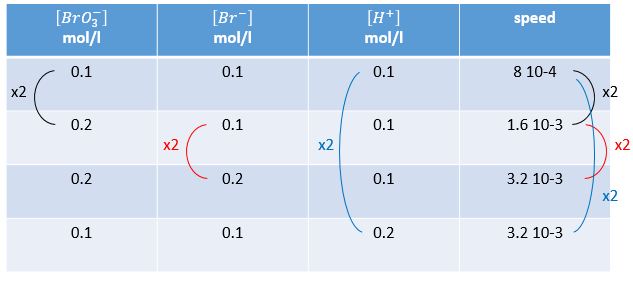
Instead of using excesses of reactants, we can do several experiments and vary one concentration each time. The reaction
is obviously not a simple reaction. The speed depends simultaneously on the three reactants BrO3–, Br– and H+. We first do the reaction with identical concentrations [BrO3–] = [Br–] = [ H+] = 0.1M. We analyse the evolution of the concentration of one species as a function of time and we only consider the variation of concentration directly after the beginning of the reaction to determine a speed of the reaction.
In a second time, we do the same reaction but modify the concentration of one reactant. The speed of reaction will change consequently and we can determine the order for each species. Ultimately when we know every order we can determine the value of k.
Model of collisions
The reactions are decomposed in elementary events. In this case the order is the stoichiometric coefficient (usually 1 or 2). Elementary events are reactions that are done in one step: everything is done during the collision between the two molecules.
For instance, the reaction between the carbon monoxide CO and NO2 is an elementary event: the oxygen atom is transferred from NO2 to the CO during a collision between the two species. When the impact occurs and the molecules were in the good orientation, the liaison N-O weakens and simultaneously a liaison is formed between C and O
The collisions between molecules don’t always lead to a new product and there are some conditions for the reaction to happen. The intermediate of reaction OCONO can be obtained only if the collision comes from a given angle: the intermediate is linear. In addition to this spatial limitation, to transfer the atom of oxygen, the liaison between O and N needs to be stretched, requiring some energy. Finally there is a variation of the number of moles of gas during this reaction: NO is a liquid and therefore there is a decrease of entropy that has to be overpassed.
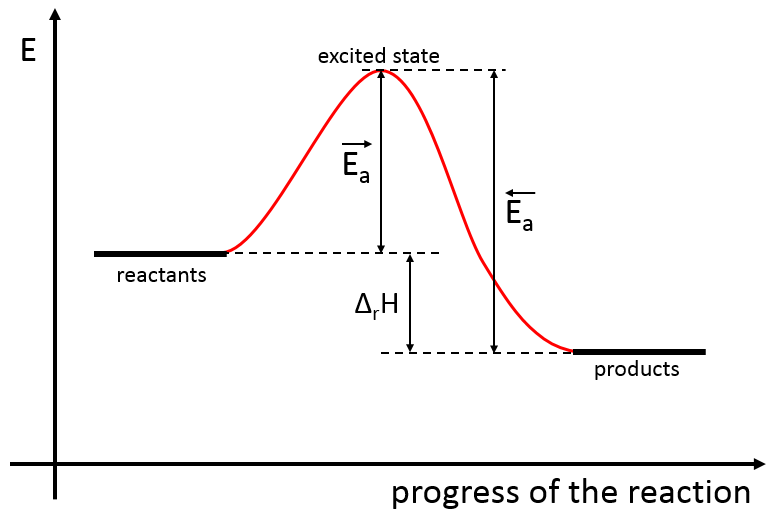
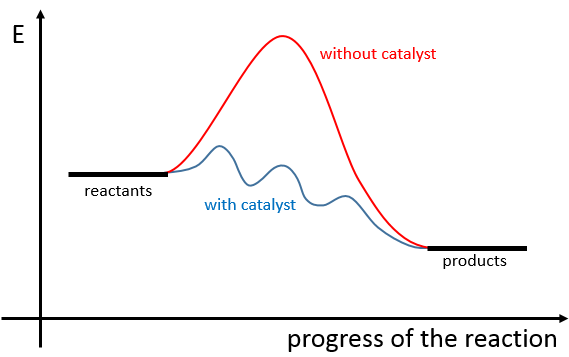
There is thus a minimum of energy that is required to obtain the reaction. This energy is called the energy of activation. One can represent the evolution of a reaction this way:
The reactants, taken separately have a given amount of energy. The products of the reaction have a lower energy. The difference of energy between the products and the reactants is the enthalpy of reaction. To obtain the products, the energy of activation is similar to a barrier that has to be climbed. At the summit of this barrier is the excited state, called this way because it is high in energy. After the excited state, the energy decreases down to the products energy that should be lower than the energy of the reactants.
To do the reaction in the other direction, forming CO and NO2, the energy of activation is much larger and the products are energetically less favourable. The difference between the two energies of activation is also equal to the enthalpy of reaction.
To surpass the energy of activation, the molecules must have enough kinetic energy. If it is the case, they do successful collisions. Remember that the kinetic energy of molecules depends on the temperature. If the temperature gets higher, a larger population of the molecules will have a kinetic energy larger than the energy of activation.
In the expression of the speed of reaction, we find these dependencies in the constant of speed k
The energy parameter is in the exponential and the spatial parameter and the frequency of the collisions are found in the constant A.
Note that slow molecules can also react if they have a large potential energy, for example a lot of energy of vibration. Instead of the kinetic energy, the potential energy is used.
As a result, if two NOBr are correctly aligned, they can form Br2 even if their kinetic energy is low because of the vibration of the liaisons Br-N.
Eventually the N-Br liaisons can be stretched simultaneously, approaching the two Br from each other and facilitating the formation of Br2.
The speed of the reaction to form hydroiodic acid from hydrogen and iodine may let us think that it is an elementary reaction.
Indeed, the exponents of the concentrations are the stoichiometric coefficients of the reactants. However, this reaction is not an elementary reaction. To have been one, the molecules would need to be aligned in one specific way and the liaisons have to break and to form at the same time. It means that 4 events have to happen at the same time in addition to the specific angle of collision.
Yet the reaction is done with a speed that let us think about an elementary event. The complete reaction is the succession of elementary events occurring one after each other.
The first step is the homolytic dissociation of I2. It is done with the help of a catalyst metal.
It was observed that the composition of the recipient can affect the speed of the reaction. The dissociation is thus done at the surface of the recipient. After the dissociation, I can now react with H2 to form H2I that can react with the second I from the first reaction to produce 2 HI.
While the last reaction is complete, the first and second reactions are reactions of equilibrium and can thus go in both directions.
The speed of the global reaction is determined by the slowest elementary event. This slow step is called the determining step and is here the last reaction:
How do we find that this speed is equal to the one obtained experimentally?
To obtain such a thing, we use two hypotheses:
- the equilibrium reactions are almost at the equilibrium: the third reaction is slower than the two first reactions and we assume that the difference of speed is such that the first reactions (almost) have the time to reach the equilibrium. As a result, we can say that for those two reactions, the speed in one direction equals the speed in the opposite direction
The ratio between the constants of reaction k1/k-1 is the global constant K1.
We can do the same for the second equation:
We can now replace the concentrations of v3 with the expressions that we found just now
The constant that was found experimentally is thus a combination of the three constants of reaction.
- the concentration of H2I is constant:
H2I is the product of the second reaction and the reactant of the third reaction. By this assumption, we assume that as soon as H2I is produced, it will be consumed by the next step of the reaction or turns back into H2 and I by the reverse of the second reaction.
We can insert this in the expression of v3.
Given that v1=v-1 (from the first hypothesis), [I]2=K1[I2] and
We have here the same expression than the one we obtained with the first hypothesis in the numerator. We can thus make the assumption that the concentration of H2I is constant if k3[I]/k-2<<1, i.e. that the concentration of I is small and that k3<<k-2. It is thus only correct at the beginning of the reaction.
We might think that the hydrogenation of Br2 follows the same kinetics but we are far from the true. Indeed,
This reaction is also a series of elementary steps
Catalyst
A catalyst is a species that is involved in a reaction but is not consumed or produced during the reaction. It helps a reaction to take place by a diminution of the energy of activation.
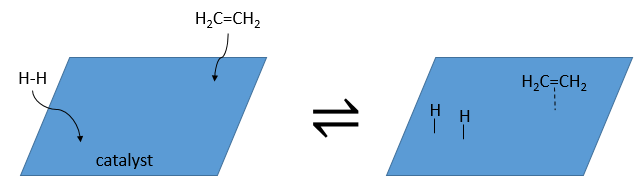
A catalyst can be in the same phase than the reactants, in this case we talk of a homogeneous catalyst, or in a different phase, as for the reaction between I2 and H2 where the catalyst is the surface of the recipient, a solid. In this second case, we talk of a heterogeneous catalyst. There are at least 4 stages for the action of the catalyst. We will see them through the catalytic hydrogenation of the ethylene.
- adsorption and activation of the reactants: the species that are in the vicinity of the heterogeneous catalyst may bind to it. In term of entropy, the binding is quite neutral: the species comes from a liquid to bind on a surface where a lot of spot are possible. There is thus a lot of possible configurations on the surface.
- Migration of the reactants on the surface: the reactants must be near to react together
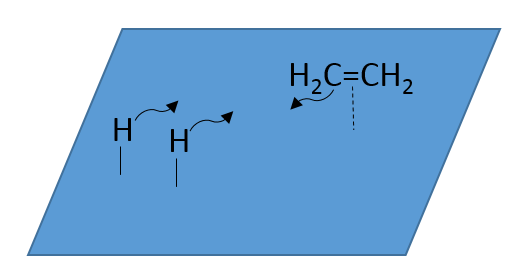
- Reactions
- Desorption of the products
In the case of a homogeneous catalyst, the catalyst is just a species that intervene during the reaction but is not consumed by it. In high levels of the atmosphere, NO acts as a catalyst in the destruction of the ozone.
Case of the ozone
The formula of the ozone is O3. This molecule is sensible to UV beams that breaks it into O2 and a radical O.. A radical is a species or a molecule that has has unpaired valence electrons and that is very reactive. They are usually the result of a homolytic dissociation, i.e. the electrons of the liaison are equally shared between the two atoms. It is so reactive that it can break nearby molecules to form a liaison. We use radicals to produce polymers (that will be seen in the corresponding chapter) and also in antibacterial products. The good point of using ozone as an antibacterial product is that it rejects oxygen O2 as waste, so it is clean for the environment.
The destruction of ozone is done in two steps: the first step is the dissociation of a radical O. under the beaming of UV photons.
The radical can react with the O2 (reverse reaction) to get back to ozone or react with another ozone molecule to form more O2.
In total, we obtain 3 O2 from 2 O3 molecules.
The radical O. is not a catalyst of the reaction even if we don’t find it in the global reaction because it is produced and consumed during the reaction. It is not a species that is already present in the system from the beginning and that remains in the system once the reaction is complete. The speed that we find experimentally is
It is not the speed that we could expect from a one step reaction. We can do the kinetic analysis of the reaction. The determining step of this reaction is the second reaction.
The concentration of the radical is difficult to determine, but we can still make the same assumptions we made with the reaction between H2 and I2: the concentration of the intermediate product doesn’t change and the first reaction is at the equilibrium:
We can insert this in the expression of the speed
Freon’s
Freon’s are small species full of halogens, CCl2F2 for instance that have a very high heat capacity and are nonpolar and inert. There have been used as refrigerant in the fridges for a long time and we thought that, as those species were inert in the labs we had no specific care to apply to them. However Freon’s are deteriorated by UV rays. In dumps, the tubes containing the Freon eventually break and the gas goes up high in the atmosphere where it is not inert anymore. The deterioration of Freon’s due to UV’s leads to the formation of radicals that will interact with the ozone.
If we sum the two last equations, we get the determining step of the deterioration of the ozone alone.
The Cl. is thus a catalyst of the destruction of the ozone and the hole in the ozone layer started to grow. The problem is that the Freon gas takes a very long time (years) to reach the higher atmosphere and at the moment we observed their effect, a lot of Freon’s were already climbing. Now the use of Freon’s is forbidden and the hole in the ozone layer is slowly decreasing in size.
Another product having an effect on the ozone is some nitrogen products of the exhaust pipes of cars. During the combustion of the fuel, nitrogen monoxide and dioxide can be formed.
Nitrogen dioxide is deteriorated by light.
Low in the atmosphere, and at the ground level, NO acts as a catalyst and generates peaks of ozone. Higher, NO catalyses the destruction of the ozone.