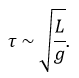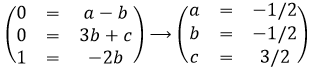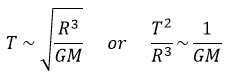Units are necessary to evaluate quantities. Obviously, a rhinoceros is heavier than a dog, but to know by how much, we need some reference units. Moreover, rhinoceroses don’t all have the same weight. We are thus in need of a consistent unit to measure the weight of objects. The same problem appears for all the possible measures: we won’t measure with precision a distance with regards to the length of bananas because bananas don’t have a consistent length, and it is not convenient for many countries to use this unit of measure. Men have thus defined some quantities as references, quantities that are constant no matter the time or the external conditions (if not explicitly described). Note that some inaccurate units of measure are still in use in daily activities when accuracy is not that important. For instance, when cooking, we add x spoons of oil without giving explicitly the required weight or volume.
On the other hand, we can measure a distance in meters or in miles, the weight in grams or in pounds. All these units have a well-defined value and can serve as reference units. While some countries as the UK or the USA use some different units, international conventions defined an international system of units (SI base units). Their biggest advantage is the simple relation between the units of different quantities. In SI, one millilitre of water occupies one cubic centimetre, weighs one gram, and requires one calorie of energy to heat up by one degree centigrade, which is one percent of the difference between its freezing point and its boiling point. In the American system, you will need to make huge calculations to calculate how much energy it takes to boil a room-temperature gallon of water because you can’t directly relate any of those quantities.
The International Bureau of Weights and Measures (French: Bureau international des poids et mesures) is an intergovernmental organization, established to maintain the International System of Units (SI) under the terms of the Metre Convention (Convention du Mètre, May 20th 1875). The organisation is usually referred to by its French initialism, BIPM. Its role is to
- establish fundamental standards and scales for the measure of main physical quantities and to conserve the international prototypes;
- compare international standards with national standards;
- ensure the coordination of the corresponding techniques of measurement;
- measure and coordinate the measures of the fundamental, physical constants involved in the above activities.
SI Units
The definitions of the reference units are mainly made to give them a well-known and fixed value.
These definitions fix the speed of light c at 299792458 m/s et the permeability of the void μ0 at 4π 10-7 H/m exactly. They also sometimes require some precisions. For instance, we point out that the cesium atom is at rest, that the carbon atoms are not connected, are at rest and in their fundamental state.
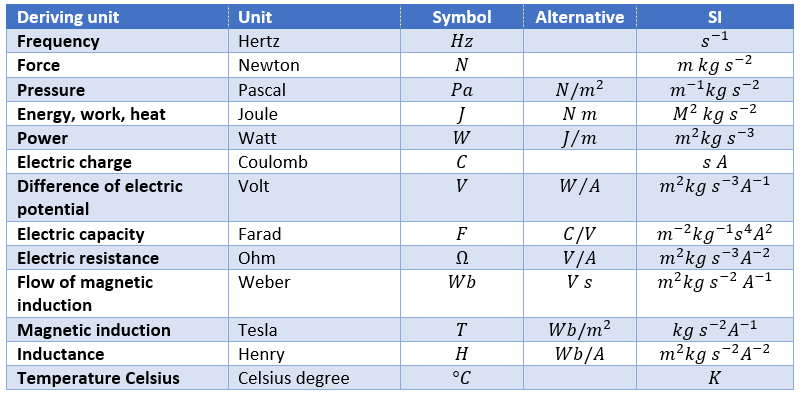
Deriving units
By commodity, some units are the combination of the SI units to express frequently used units.
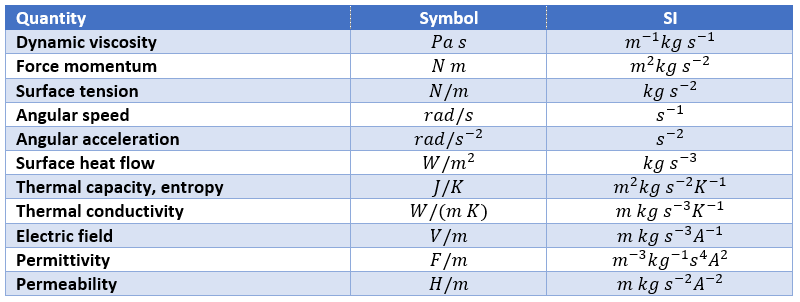
Finally, there are some quantities without specific unit names
We can point out a few specific units:
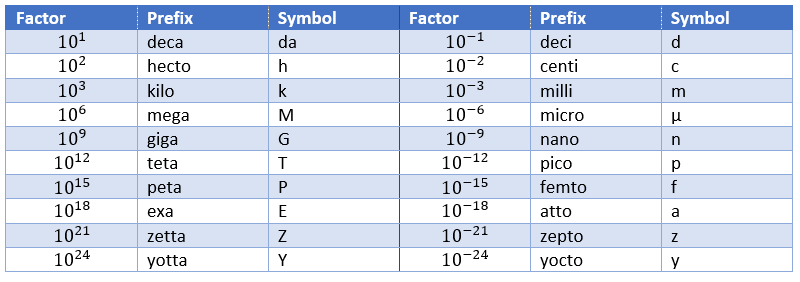
To put an end to this section, we will list the prefix of multiples of the SI units.
Dimensional analysis
The existence of the IS system means that all the other physical quantities have units that are homogeneous functions of these base units. A function is homogeneous if, making a scale change on all of its variables: x1 → λ1x1, x2 → λ2x2, x3 → λ3x3, … the function itself changes of scale: f(λ1x1, λ2x2, λ3x3,…) = λ1α1 λ2α2 λ3α3…f(x1, x2, x3,…). The units of any quantity, let’s call it Qr is thus always expressed by a relation like
So if we know the units of one physical quantity, and admitting that there is a relation between this quantity and other variables, and knowing the units of those variables, we can guess the relation between the quantities.
For instance, we observe the swinging of one object attached to one string: a pendulum. The pendulum oscillates because it falls and it is restrained by the string. We want to determine the relation between the times the pendulum takes to make one oscillation, i.e. the period, to the parameters we guess as important: the mass M of the object, the length L of the string, and the gravity acceleration g that affects each object on the planet. The units of the variables are kg for the mass, m for the length, and m/s² for the acceleration. The period is a time and thus its unit is s. The relation between the variables and the period should be something like this:
As there is no kg at the left of the equality, and it is present at the right side of the equation with the exponent a, then we conclude that a=0. Looking at the seconds, their exponent is 1 at the left and -2b at the right, b is thus b=-1/2. Finally, there is no m at the left while it is present at the right side of the equation, thus 0=b+c. As we determined the value of b, we have that c=1/2 and that the global relation is
From our dimensional analysis, we determined that the mass of the object has no influence on the period of the oscillation of the pendulum. Note that we did not write the equal sign: the dimensional analysis doesn’t give the true law; it gives clues on the variables but there can still be numerical factors that can be determined experimentally. On the other hand, the dimensional analysis allows to identify wrong laws not respecting the units of the quantities.
Let’s analyse a second example: the period T of revolution of planets around the Sun. First we identify the important parameters involved in the problem: the mass M of the Sun, the distance R between the planet and the Sun, and a constant G giving the gravitational force. The units of the parameters are respectively kg, m and kg-1m3s-2. The period is given in seconds s. The law should be of the form T ~ MaGbRc. For the units, we have the relation
The next step is to identify the exponent of each unit at the left and the right side of the equation:
The law is thus written
This relation is the expression of the Kepler’s law that describes the trajectory of planets of the solar system.
Scales and orders of magnitude
An experimental approach is to estimate the order of magnitude of variables that appear in physical processes. Either we measure the characteristics of one well known property of the matter, or we determine a transition zone between two models of description.
For instance, we can regroup the matter as solids, liquids and gases. One major difference between these three phases is their density, i.e. the mass of the matter for a given volume, given in kg/m3. We can thus regroup liquids as matter with a density with the order of magnitude around 103kg/m3 (at T=293K, water: 1003kg/m3, olive oil: 910kg/m3, sulfuric acid: 1834kg/m3,…)while gases have a density of order 1 (at T=273K, air: 1.2kg/m3, CO2: 1.98kg/m3, methane: 0.72kg/m3,…). Between solids and liquids, there is a factor 10 in density (at T=293K: iron: 7893kg/m3, copper: 8954kg/m3, gold: 19320kg/m3,…). We will want to determine the temperature at which a solid becomes liquid, i.e. its melting temperature.
As the interactions between particles of a solid differ from the interactions between particles in a gas, laws are not the same at the microscopic scale than in the astronomic scale, not because the interactions mysteriously disappear, but because we can neglect some interactions. For instance, imagine an interaction between particles that depends directly on the distance between two particles and one interaction that depends on the third power of the distance. If the distance is small, both interactions will have an effect, but as soon as the distance gets large, we can neglect the first interaction.