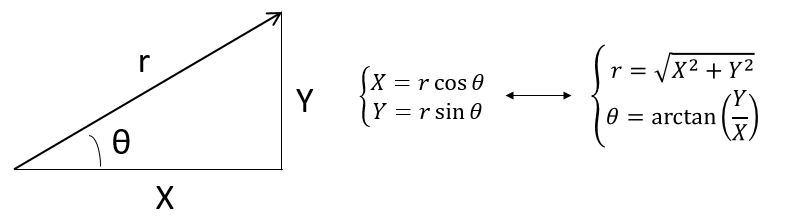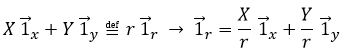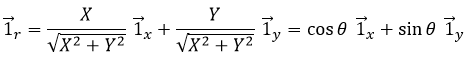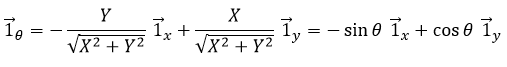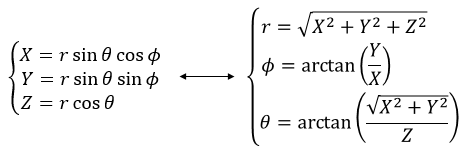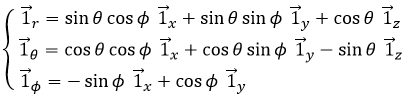The first formalism that has to be known in physics is the formalism of the motion. A formalism is associated with a certain rigorous mathematical method, defining symbols and rules that are commonly accepted, in the goal that everybody understands immediately the discussed matter. We will not be interested in the prediction of the motion nor its cause, but in its description alone.

In this section, we consider that every object can be considered as a dot without volume.

The position

The motionis the history of the position of an object, the succession of the positions of this object over the time. To define the position of the object, we need a reference system in which we can give the position: coordinates. Several systems of reference exist and there are several ways to calculate the coordinates of objects. All of them are corrects but some are more convenient than the others. During a trip, you won’t give your position with regard to the sun, the same is true in physics.

Several coordinates are generally necessary to determine the exact position of one object. If you say that you are 10km from Paris, you give an information on your position but we are lacking at least one coordinate to determine your position. Usually you need one coordinate by dimension of the system.

One dimension

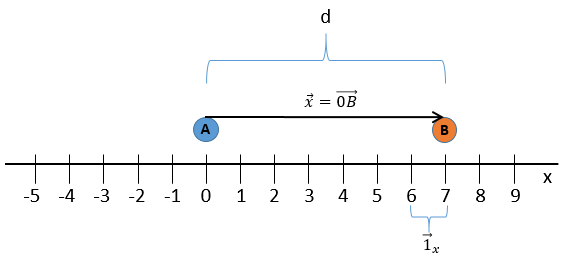
We choose one origin to the coordinate system, the zero point. It is convenient to choose the initial position of the object A as the origin but it is not mandatory. Next we choose a direction that will be the positive positions. In the opposite direction we have the negative positions. Still for convenience, the positive positions are placed in the direction we guess the object will move towards. Imagine that the object moves towards another object B placed at a distance d. The position vector indicates the distance between an object and the origin, and points towards the object with an arrow. The symbol for vectors is topped by an arrow pointing to the right. The position vector for B is

Where  is the unit vector in the direction x (the single direction in this problem).

Two dimensions

The second coordinate is usually orthogonal, perpendicular to the first coordinate to avoid a maximum of angle problems and to benefit the simplicity of the calculation for right triangles. Each coordinate has a direction.

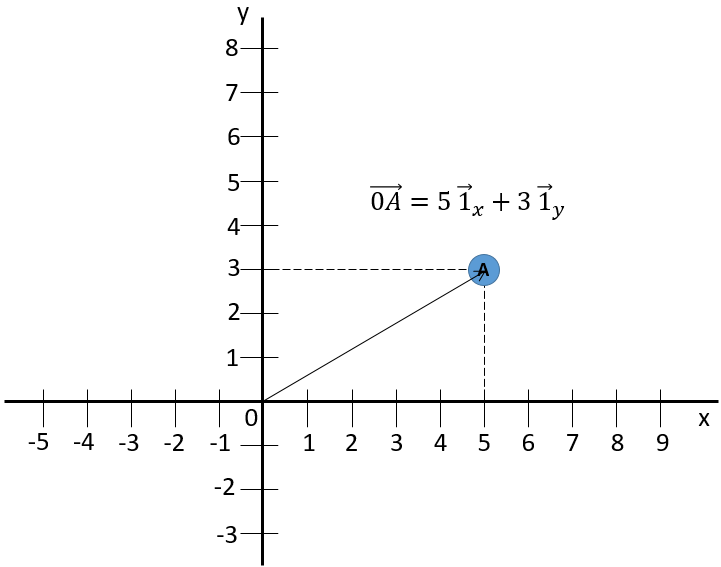
The position vector is now defined by two components from which we can calculate its length if desired.

The addition sign between the two unit vectors is seen as “followed by” and not like the addition of two usual numbers. Another way to write coordinates is to put them in brackets. If we do this, then we don’t write the unit vectors.

This system of reference, the Cartesian system, is not the single one that can be used at two dimensions to determine the position of an object. We can also position the object from its distance r to the origin point and an angle θ from one axis. This reference system is called the polar system.

It is possible to determine the relation between the coordinates X;Y in the Cartesian system and r;θ in the polar system using the relation defining the cosine, the sinus and the tangent:

The unity vector  can thus be calculated.

or

We can also define the unit vector :

Both polar unity vectors depend thus upon θ that should thus be chosen conscientiously.

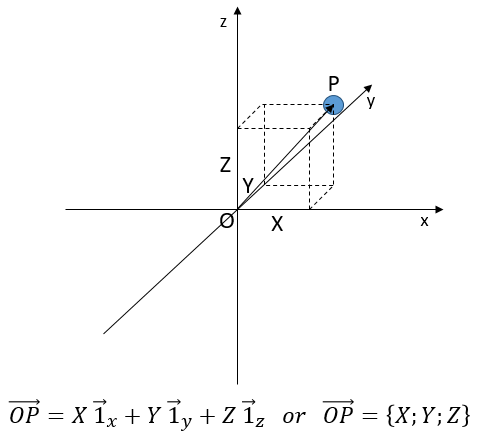
Three dimensions

A third coordinate is added in the reference systems. In the Cartesian system, we add a coordinate that is orthogonal to the two previous ones.

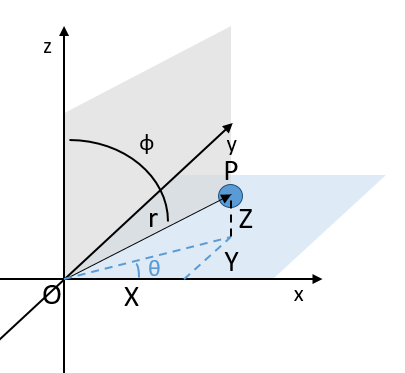
In the polar system, we need a second angle to determine the position of an object. We take the first from the axis x in the xy plane and the second angle is taken from the z axis in the zr plane of the object.

Again, the Cartesian system can be associated to the polar system.

The unit vectors are defined as