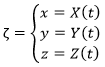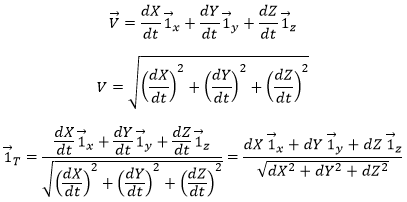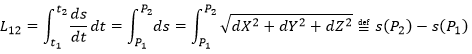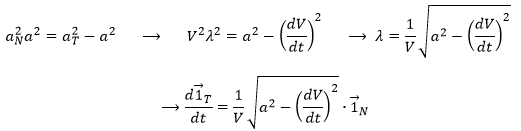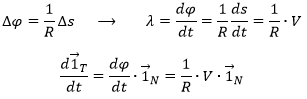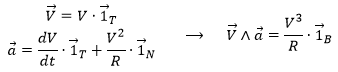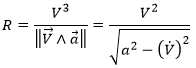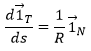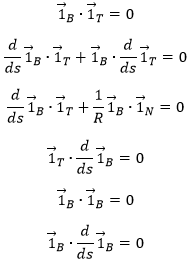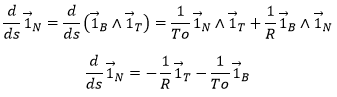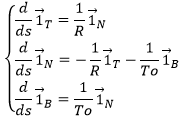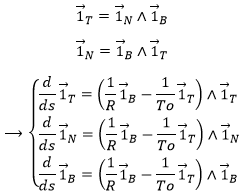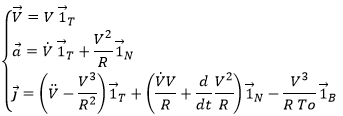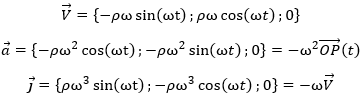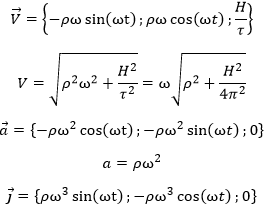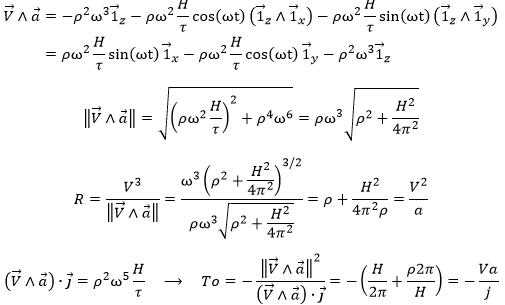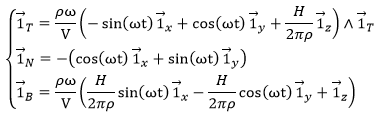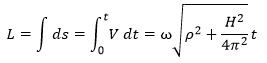Abstraction made of the time, the geometry is preponderant. In this section, we will discuss a lot about vectors and we define the tangent, the normal and the binormal.

The tangent

The trajectory is the path a moving object follows through space. Let’s analyse this curve ζ from the geometric point of view. The trajectory curve can be defined by

If we take two consecutive positions,  and , the average speed is the vector carried by the rope  The instantaneous speed on her side is a vector tangent to the trajectory.

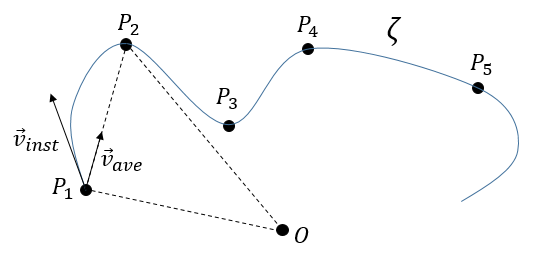
The direction of the speed vector defined thus the tangent to the trajectory. We can get rid of the length of the speed vector and keep its direction by dividing it by its intensity. As a result, we obtain a vector of length 1 tangent to the trajectory.

In the Cartesian system, it corresponds to

In this last expression, the time is not explicitly present. If we defined ds as the instantaneous displacement  we can write

 

The length L of the trajectory is the sum of the lengths of the average displacements and, in the limit, to the integration of the lengths of the instantaneous displacements.

The length of the trajectory s is a parameter intrinsically related to the curve ζ as it doesn’t depend upon the choice of the origin point O, nor of the parameterisation of the curve ζ. It shows, in its infinitesimal version ds, the distance to make on the tangent of the trajectory.

The normal

The vector  being defined, how do we express the geometric aspect related to the acceleration? By construction, the speed vector is tangent to the trajectory of the position vector. The acceleration vector is thus also tangent to the trajectory of the speed vector. How do we represent that in the space?

Let’s derivate the speed vector, giving explicitly its norm V and the direction :

The first term is proportional to  and is thus parallel to the speed vector. The second term is necessarily perpendicular to it. Indeed, the trajectory of  cannot be anywhere else than on a sphere because, by definition, its length does not change. As its derivative is tangent to this trajectory, it is thus tangent to the sphere and thus perpendicular to the radius of the sphere, i.e. to the vector .

We can define the normal vector  as the derivative of the tangent vector.

λ is still to be determined.

• Algebraically

The acceleration  is thus the sum of one tangent part  and one normal part , perpendicular to the first part.

The length of the square of the acceleration is thus given by (the vector product of two perpendicular vectors gives zero)

And then

• Geometrically

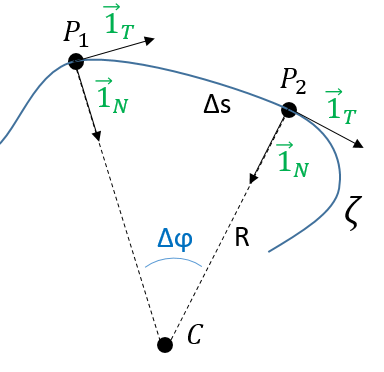
Given two consecutive positions of the point P on the trajectory ζ:  and , and the direction of the speed  and  at the corresponding positions. The tangent unit vector , by definition, doesn’t change its length. However, its direction changes: it turns by an angle .

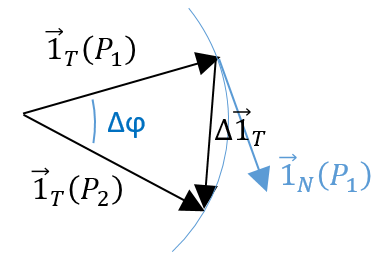
The two tangent vectors delimitate a plane P in which is also their variation . With these three vectors, we can build an isosceles triangle and thus evaluate the length of : 2 sin(/2) and its angle with : π/2-/2.

At the limit, when P₂ tends towards P₁, the length of  becomes  and the angle becomes thus π/2, i.e. becomes perpendicular to . As a result we can write

λ corresponds thus to the angular speed of rotation of the tangent vector. To be more accurate, we see that if we extend the normal in P₁ and in P₂, they meet at the point C, and that this point C is, at the limit of , the centrum of the tangent circle of the curve ζ in P₁ and P₂. The angle  equals the length of the arc ∆s divided by the radius R of the circle. As a result,

The radius R is called the curvature radius of the trajectory ζ at a given point. 1/R is called the curvature of ζ and the limit plane P formed by the tangent vector and the normal is called the osculating plane of the trajectory ζ.

The binormal

As the tangent  and the normal  are defined, we can build a vector perpendicular to those two vectors: the binormal . To do so, we make the vector product:

This vector is perpendicular to the plane P of the trajectory and is oriented so that the three vectors  can be overimposed to the three Cartesian vectors . Knowing the definitions of the speed and of the acceleration, we also can say that

What allow us to determine the equation of the curvature radius R

The dot over a variable means that it is its derivative over the time. Two dots will mean the second derivative, etc. The readability of the equation can be eased this way. In terms of components of the speed and of the acceleration, we have

Frenet formulas

The three vectors obtained this way form the referential of Frenet that follows the point P on its trajectory. The referential is thus intrinsically related to the trajectory. The relation we have seen earlier

becomes, if we use the parameter s of length on the trajectory

What happens to the other vectors of the referential in the movement on the trajectory? As the vectors are orthonormal to each other, we can determine them from scalar products.

As a result, the derivative of the binormal vector is perpendicular to the binormal  and to the tangent  at the same time. It is thus only proportional to the normal . We define the torsion radius To by analogy with the curvature radius R:

Remember that to define the vector  we chose R positive; to define the vector , we used the two vectors  and . As a result, we don’t have the choice for the sign of To, that can be positive or negative.

The derivative of  can be easily calculated:

We can now write down the equations of Frenet:

We can use the fact that the vectors are the scalar product of each other.

In terms of speed , acceleration  and over-acceleration , we have

What leads to

That was the result obtained previously. We also find that

Canonic applications

The uniform circular motion

The point P moves with a constant speed on a circle of radius ρ and of centre O. The angle the point travels by unit of time is thus constant. We define the angular speed ω as

If we choose the x-y plane to place the circle and O as the centre of the Cartesian system, the position of the point P is given by

The speed, acceleration and over-acceleration are

The osculating plane is the one we chose, obviously.

The distance s made on the curve is given by the length of the arc ωρ. Indeed:

The curvature radius R equals ρ by construction, confirmed algebraically:

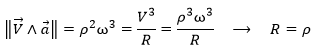
The torsion 1/To equals zero because the trajectory is in the plane z=0.

We can observe that

• The acceleration is perpendicular to the speed,
• The speed (not the angular speed) is not constant
• The modulus of the speed is constant
• The acceleration is not constant
• The modulus of the acceleration is constant
• The acceleration points towards the centre O (it is centripetal)
• The acceleration is proportional to the radius of the circle (at a fixed ω) but inversely proportional to it at fixed V.

The regular helix

If we turn uniformly in the x-y plane while moving in the z direction with a constant speed, we obtain a movement of coiling around a cylinder. The time required to make one turn of the cylinder is the period τ and the distance made in the direction z over this time is the step H. The equation of the position of the point P is given by

At the exception of the movement on the z axis, this equation is thus the same than the one or the circle, given that ω=2π/τ. We can easily write the equations for the speed, acceleration and over-acceleration:

We note that some of the simple relations we had for the uniform circular motion are no longer valid: . However, the acceleration is still perpendicular to the speed () and the over-acceleration perpendicular to the acceleration (). The acceleration points towards the axis of the cylinder and is proportional to its radius ρ (which is different from the radius of the trajectory). Concerning the curvature radius R and the torsion radius To, we have

The torsion and the curvature are thus constant during the movement.

The Frenet vectors are given by

 The length L of the helix is easy to calculate because the modulus of the speed is constant:

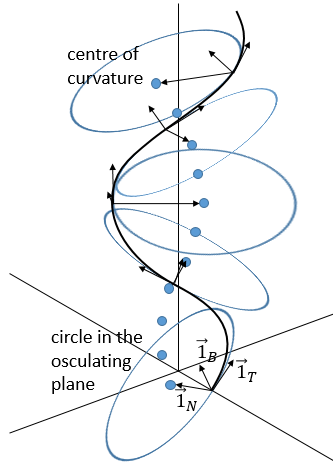
The following figure shows an example where the three Frenet vectors, the position of the centre of curvature C and a few circles of centre C and of radius R in the osculating plane P.

We can visualise the torsion by the rotation of the osculating plane. The normal vector is the one pointing towards the centre of the curvature, the tangent vector is the one tangent to the trajectory and the vector product of these two vectors gives the binormal vector, perpendicular to the circule tangent to the trajectory.