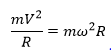When an object has a circular motion even though its speed is constant, it is nonetheless accelerating because according to newton’s 1st law: an object continues in its state of rest or uniform motion unless acted on by an external force. So if the object was to be free in space then of course it will continue to travel tangentially in the direction that it has just before.
But if it changes the direction of the velocity ( the change of the velocity is acceleration). In fact,this acceleration is always towards the center of the circle and it’s called centripetal acceleration. And if we have an acceleration then the newton’s second law must be applicable which says: the force is equal to mass times acceleration (F= m.a ) then the centripetal force = mass X centripetal acceleration.
If the speed of objet is![]() and the radius of circle is R, then if the objet travels around one time, the distance that it travels is =2πR, it’s simply the circumference of the circle and imagine it does that in 60 seconds,so the velocity will be
and the radius of circle is R, then if the objet travels around one time, the distance that it travels is =2πR, it’s simply the circumference of the circle and imagine it does that in 60 seconds,so the velocity will be ![]() in m/sec.
in m/sec.
The another way of measuring is the angular speed and we know that the whole circle is 360°=2π. We use radians to measure angular speed, radians =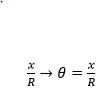
How many radians are there in a full circle? Full circle will be 2πR.
Angular speed: is designed by ω and ω=2π/t radians/second and we know that V= 2πR/t that means V= ωR, So this formula shows the relationship between the V (orbital velocity) and ω (angular velocity) .
Frequency (ƒ): is the number of cycles per second, we know that ω is the number of radians per second and we know that 2π is the number of radians per cycle then ƒ= ω/2π and we can write ω= 2πƒ.
Period (T), is the amount of time it takes to do one cycle And T= 1/ƒ so if ω=2πƒ then ω=2π/T
Centripetal acceleration:
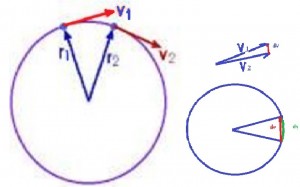
Imagine the objet with a speed![]() at point a and after a short distance it will be at point b which will have an angle dθ (a very small angle).The distance travelled will be called dx (a small distance).
at point a and after a short distance it will be at point b which will have an angle dθ (a very small angle).The distance travelled will be called dx (a small distance).
The time of travelling = dt, so the objet travels a small distance (dx) sweeping out an angle called (dθ) and it does that in a short time (dt).
When it will be at b, the speed is still![]() because it doesn’t change the speed but it will be now in a different direction and if the speed changes that means the objet has been subjected to an acceleration.
because it doesn’t change the speed but it will be now in a different direction and if the speed changes that means the objet has been subjected to an acceleration.
Acceleration is the change of velocity during the time. To calculate the difference between two vectors we must put them tail to tail.what we are looking for is the streight line dy we know dθ= dy/v (small circle with r=v )
If dθ is very small, then the arc length y becomes the straight line dθ=dv/v
dx =Rdθ (=Rdv/v) dx= Vdt ⇒Rdv/v= vdt ⇒Rdv/dt= ![]() ⇒ dv/dt =
⇒ dv/dt =![]() = a
= a