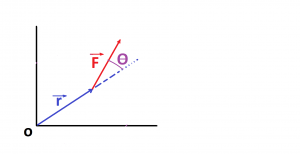
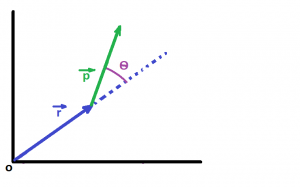
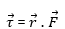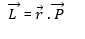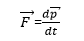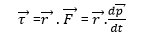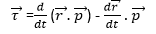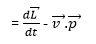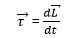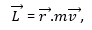Definitions: the torque and angular momentum are defined as vector products of position, force and momentum. Suppose a forceacts on a particle whose position with respect to the origin 0 is the displacement vector . Then the torque “about the point 0 and acting on the particle,” is defined as:

Now suppose the particle has a liner momentum P relative to the origin. Then the angular momentum of the particle is defined as:

The direction of  and  are given by the right-hand rule for cross products.

Relationship:  =  Using the definitions of torque and angular momentum, we can derive a useful relationship between them.

Starting from Newton’s second law, written in the form:

The torque is:

This can be rewritten using the expression for the derivative of a cross product:

Now  so   (because the vector product of parallel vectors is zero), so the torque is:

Thus the time rate of change of the angular momentum of a particle is equal to the torque acting on it. 

Motion confined to a plane: 

The expression   for a particle takes on a scalar appearance when the motion of the particle is confined to a plane.

Consider a particle constrained to move only in the x-y plane, as shown in Fig.2. the torque on the particle is always perpendicular to this plane as is the angular momentum .

Equivalently, we say that  and  have only z-components. Since their directions remain constant, only their magnitudes change. Then:

This equation holds only if are in the same plane; if not (and they won’t be for non-planar motion), the full Eq. must be used.

Circular motion of a Mass: The torque and angular momentum for the special case of a single particle in circular motion can be easily related to the particle’s angular variables. Supposed a particle of mass m moves about a circle of radius r with speed v (not necessarily constant) as shown in Fig.3. The particle’s angular momentum is:

But since  are perpendicular, the magnitude of L is:

And the direction is out of the page. This equation  may be rewritten in terms of the angular velocity (since ) as:

Similarly, the torque is:

Where α is the particle’s angular acceleration.

Systems of Particles

Total Angular Momentum:  The total angular momentum of a system of particles is simply the sum of the angular momenta of the individual particles, added vectorially. Let  be the respective angular momenta, about a given point, of the particles in the system. The total angular momentum about the point is:

As time passes, the total angular momentum may change. Its rate of change , will be the sum of the rates  for the particles in the system. Thus  will equal the sum of the torques acting on the particles.

Total Torque: The total torque on a system of particles is just the sum of the external torques acting on the system. The torque due to internal forces is zero because by Newton’s third law the forces between any two particles are equal and opposite and directed along the line connecting them. The net torque due to each such action-reaction force pair is zero so the total internal torque must also be zero. Then the total torque on the system is just equal to the sum of the external torques:

For the system, then:

In words, the time rate of change of the total angular momentum about a given point, for a system of particles, is equal to the sum of the external torques about that point and acting on the system.

Rigid Body Motion About a Fixed Axis: A rigid body is a system of particles whose positions are all fixed relative to each other. Since   for each particle in the body, we may write for the total angular momentum:

Where we have assumed that the body is rotating about a fixed axis with angular velocity :   

And, since the axis of rotation is fixed, equations with a scalar appearance         hold for the torque: