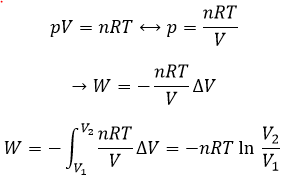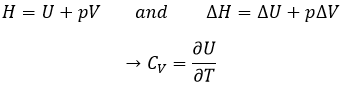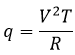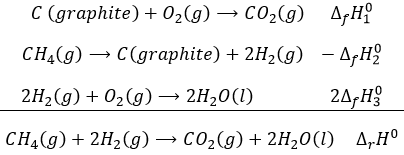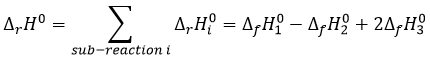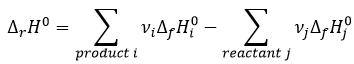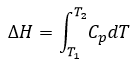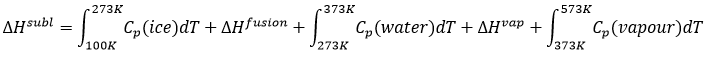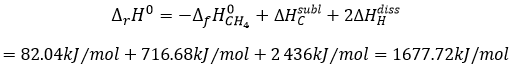The thermodynamics is the study of the transfer of energy and especially of heat. It is important to make the distinction between heat (q) and temperature (T). The temperature reflects the motion of particles and is connected to their kinetic energy, but the temperature is no energy. Heat is an energy that exist if there is a difference of temperature, by convention from the hottest to the coldest component. The units of the heat is the units of an energy, i.e. joules J=N.m.

When it comes to transfers of energy, we have to define the system in which we are working. The system is the part of the universe that we are analysing and we distinct it from the environment that is the rest of the universe.

3 kinds of systems can be differentiated

– Isolated system: there is no exchange between the system and the environment

– Closed system: exchanges of energy are possible between the system and the environment

– Open system: exchanges of energy and/or matter are possible between the system and the environment

A system is exothermic if it liberates heat. If it takes heat, the system is endothermic.

The thermodynamics is governed by 3 major principles.

First principle

Conservation of the energy: The energy of the universe is constant.

It means that a process occurring in an isolated system doesn’t involve any variation of energy. If exchanges of energy are allowed with the environment, i.e. in closed systems, the intern variation of energy in a system is composed by the heat q and the work W to make the process.

If the system also allows exchanges of matter, a term dE_m representing the energy of the flow of matter is added.

The variation of energy is a state function. It means that this function does not depends on which way the system reached this point, but only on its initial and final state. W and q are not state functions and depend on the way the system evolves during the process.

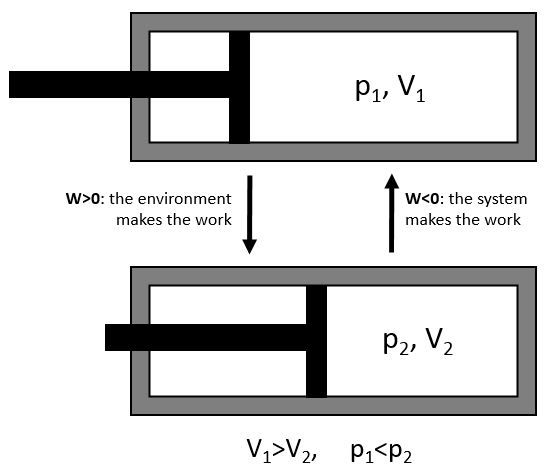
The work has a negative value if it is made by the system. For instance, imagine a volume in which a gas is stored.

To compress the gas, the environment has to apply a force on the piston. W is thus positive in this case. If the piston is free of movement, the gas in the volume applies a pressure on the piston to increase the volume of the system. In this case W<0.

The work is an energy, so it is basically a force multiplied by a distance. If we consider the dilatation of a perfect gas the work would be

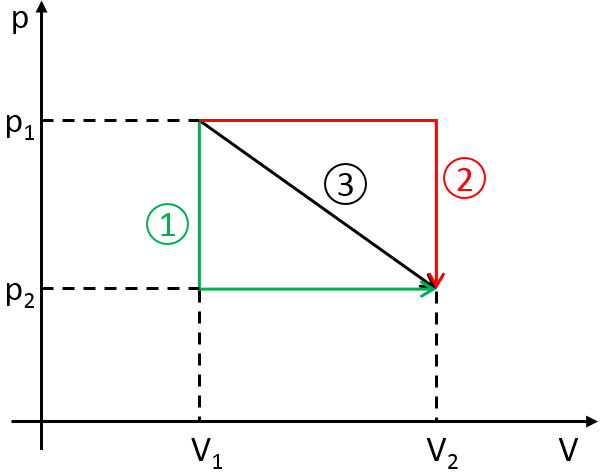
To move from a state (p₁,V₁) to (p₂,V₂) several paths can be taken.

Those ways are equivalent in the term of variation of energy because the energy is a state function: the final state and the initial states are characterised by an energy that does not depend on how they were obtained. Yet, the work and heat are different for each path.

Indeed, on the path 1, W=-p₁(V₂-V₁). On the path 2, the work is W=-p₂(V₂-V₁). As p₂<p₁,  it means that more work is required on the path 1 and that there is a larger production of heat on the path 2. On the path 3, the volume and the pressure vary simultaneously. We use the law of perfect gas to determine the work in this case. Path 3 is in fact an isothermal curve, where q=0.

Now, let’s talk about heat. In previous chapters, we discussed about the heat capacity. It is the energy required to increase the temperature of the substrate by one kelvin/degree. We distinguish the heat capacity at constant pressure C_p and at constant volume C_V.

Note that we used partial derivatives ∂/∂T instead of derivatives d/dT. A partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant.

H is the enthalpy of a state and ΔH is the variation of enthalpy of the process (that can be a reaction or a transition of phase for instance) at a constant pressure. ΔH is thus equivalent to q_p, the subscript _p indicating that it is the heat at p=cst.

The equation for the enthalpy is

For perfect gases, pV=nRT, so

Given that C_p= ∂H/∂T we find a relation between C_p and C_V for perfect gases

For solids and liquids, the variation of volume is negligible and C_p»C_V.

Calorimetry

An enthalpy of reaction ΔH° is associated with each reaction.

The ° indicates that this value is the enthalpy found for one mole of reactant, at 1atm. The enthalpy of a reaction can be measured experimentally by calorimetry. During calorimetry, a reaction is made in an isolated system (no exchanges with the environment). The variation of temperature in the system is measured and from this measure we can deduct the heat of reaction. For instance, the neutralisation of HCl by NaOH is exothermic (ΔH°<0), meaning that this reaction generates heat. It is thus possible to measure a variation of temperature ΔT during the reaction. To do so, we use an isothermal and closed recipient in which the reactants are initially separated. The temperature in the system can be read on a thermometer. The temperature is not directly taken in the reactive solution. Usually, the reaction takes place in a recipient (called the calorimetric bomb) that is surrounded by water. The whole setup is in the isothermal recipient. The variation of temperature is measured in the water. When the reaction takes place, the elevation of temperature is recorded in function of the used amount of NaOH. With the adapted setting, we can measure q_p (p=cst) or q_V (V=cst).

If the pressure is kept constant, the variation of temperature ΔT is proportional to q_p.

As we consider a liquid phase, q_p»q_V.

C_V can also be determined experimentally: A given heating is applied in the solution through an electric resistance.

With V the tension and R the resistance. The variation of temperature ΔT due to this heating depends on the heat capacity of the liquid.

So if we know the applied tension and the resistance, the measure of the variation of the temperature gives us the value of Cv.

Law of Hess

The energy and the enthalpy are state functions, i.e. their value does not change in function of the path/process and are only a function of the state of the system. It means that if we perform a cycle of transformations, obtaining at the end our initial compounds, the sum of the variations of enthalpy of the processes of the cycle is equal to 0kJ/mol. Note that the absolute value of the enthalpy of a body cannot be determined. Only variations of enthalpy can be determined. It means that we can determine the value of enthalpies with regard to a given process and thus that the enthalpy of formation of a molecule is determined in comparison with other reactions.

By convention, the enthalpy of formation of simple bodies composed of one single element (for instance O₂, H₂,Na,etc but H₂O not because there are two different atoms in the molecule) in their standard state equals 0kJ/mol. The standard state is the most stable state of a body at 25°C and 1 atm. In the nature, some elements can be found in several states but the body in its normal state at 25°C and 1 atm alone has a Δ_fH°=0kJ/mol. For instance, the carbon can be found as graphite and as diamond.

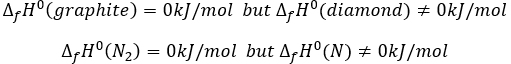
We say that the graphite and the diamond are two allotropes of carbon. The atoms are bond together differently in those two solids. Between them, the standard state of the carbon is the graphite because the diamond is not formed in this range of pressure and temperature. Technically, the notion of standart state depends on the temperature and pressure, and the diamond will be the standard state of carbon for very high pressures but we commonly use the “standart state” term for the normal conditions of temperature and pressure.

For molecules that are not in their standard form, the enthalpy of formation is the enthalpy of the reaction producing the molecule from the elements in their standard state that compose it.

The enthalpy of this reaction is thus the enthalpy of formation of the carbon dioxide CO₂: it is the reaction that generates carbon dioxide from the elements in their standard state that compose CO₂.

This reaction is the reverse of the formation of the methane CH₄. The enthalpy of reaction is simply minus the enthalpy of formation Δ_rH°=-Δ_fH°.

The enthalpy of this reaction is twice the enthalpy of formation of the water because we form two moles of water with this reaction. The enthalpy of reaction is given in kJ by mole of product

If we combine those three reactions, we obtain the cycle of Hess. The enthalpy of this final equation is the sum of the enthalpies of formation of the three sub-reactions:

We can sum up the enthalpies of the sub-reactions to obtain the enthalpy of reaction of formation of CO₂ and H₂O from CH₄ and O₂.

In a general way, the enthalpy of a reaction is the sum of the enthalpies of formation of the products minus the enthalpies of formation of the reactants, each one multiplied by its stoichiometric coefficients.

We clearly see here that those two expressions are identical

Don’t forget that the enthalpy is a state function but depends on the temperature and that a reaction can be favoured by a variation of temperature.

At a constant pressure, the enthalpy can thus vary if there is a variation of temperature

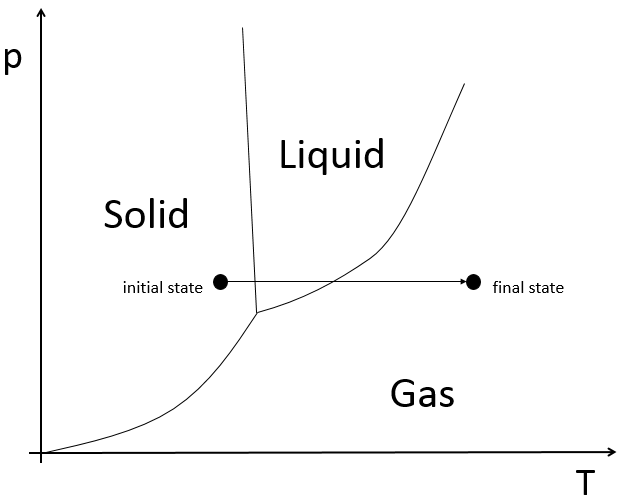
A change of state will also increase the enthalpy of reaction.

If we want to change ice into vapour, i.e. sublimate ice, at a constant pressure=1atm,

 the enthalpy will be

The triple point is a particular point where ice, vapour and water coexist and where

From that point, we can find the enthalpy of one phase transition from the other two.

Energy of liaisons

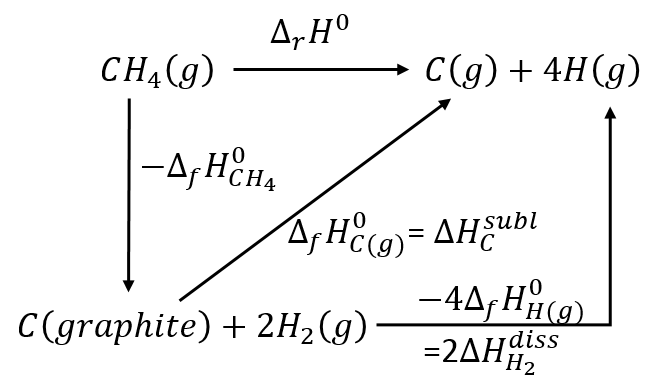
We have seen that we can find the enthalpy of reactions from the enthalpies of formations of each participant of the reaction. There should thus be reactions that allow us to determine the energy of chemical bonds. For instance, the reaction

is basically the scission of 4 C-H bonds. Nothing else has been done during this reaction. We can determine the enthalpy of the reaction Δ_rH⁰ from the enthalpy of formation of CH₄, C and H. We have seen earlier the inverse of the reaction of formation of the methane

From that reaction, we still need to dissociate the molecules of H₂ and to sublimate the graphite into a gas.

As there are 4 C-H bonds that have been broken, each bond has an energy of 419kJ/mol.

Fuels

The thermochemistry is a vast domain of the chemistry that finds applications in fuels for example. We can determine the energy of liaisons during the combustion of molecules composing the fuel, exactly the same way as we did for the liaison C-H. The hydrazine N₂H₄ is a nitrogen molecule used as fuel for space propellers.

Most of the nitrogen compounds have a positive enthalpy of formation, meaning that we need to spend energy to generate them. It also means that they will easily break to form N₂ and H₂O, generating a lot of energy. An exception is NH₃. What is the energy of the reaction? O₂ and N₂ are in their standard form, meaning that their Δ_fH⁰=0kJ/mol. The enthalpy of reaction is thus

This reaction generates heat because the energy of the formed liaisons is greater than the energy of the broken liaisons. We broke 4 N-H bonds to form 4 O-H and the N-N bond became a triple liaison N≡N. The O-H and N≡N liaisons represent respectively 460kJ/mol and 941kJ/mol.

Because of all the energy that has been generated by the reaction, the water changes of phase and becomes gaseous. The propulsion of the space shuttle is not only the result of the energy but comes from the expansion of the gas: from one mole of gas we make 3 moles of gas. The gas expand very quickly because of the heat (pV=nRT), generating the explosion in the propeller.