1st Year, College - Main subjects, Mathematics

Chapter 1: Probability ( basic review of sets)

Written by admin on .

Definition :

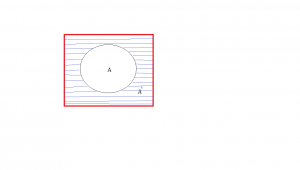
A set is a collection of mathematical or every kind of elements  e.g   A = {1,2,3,4,6,Δ,a} .1,2,3,4,6,Δ,a  are called elements of the set A and the size of elements is the absolute value of A = !A! (that is the absolute avalue of  total number of elements) .In this case the size of A is 7

Operation on sets:

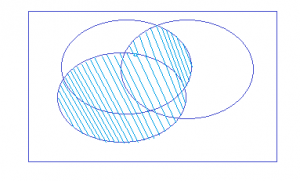
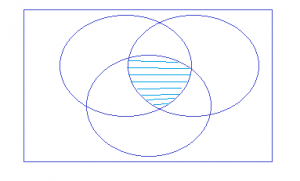
There is a kind of mathematical rules of sets:  ∩= Intersection,  U= union eg If A and B are sets  AUB = is the set of all X such that X is an element of A or X is an element of B  A∩B= is the set of all X such that X belongs to A and X belongs to B. Sometimes we can do a kind of venn diagrams to illustrate sets :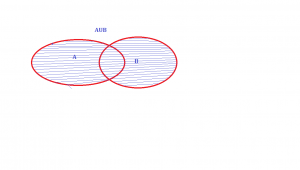VENNE DIAGSometimes all sets belong to a universal set eg the universal set U then A complement is a set of X belonging to U such that X dose not belong to A

set universalLaws of set operations :

A U (B ∩ C) = (A U B) ∩(A U C)

image 5

That means every thing in A plus every thing in the intersection of B and C

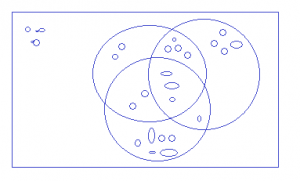
AUBUC = ¦A¦+¦B¦+¦C¦—¦( A∩B)¦—¦A∩C¦—¦B∩C¦+¦A∩ B∩ C¦

 image 4                                                                                                            Inclusion/Exclusion Inclusion/ Exclusion for n sets!

Ex. Uni  foot team has 11 students taking chemistry (C) ,12 students taking mathematics (M),12 students taking physics (P). If 7 take C and P, If 4 take M and P, If 5 take C and M, If 3 take all three, If 3 take none of these.Haw many are in the team?

so without any formulas we have 25(Number) in the union (total =25)

image 6

Partition of a set A:

the idea of partition is to subdivide a set in pieces

Def: a partition of the set A is a set of subsets

If C is a subset of B that means if X belongs to C then X belongs to B. the addition of subsets equals the original set

There are conditions to that : all the subsets of A must be  disjoint. so A1+A2+A3+…………………………..Ak= A

Ex :

Let’s flip a coin 3 times then the possible outcomes are 8 possibilities (TTT, TTH, THT, THH, HTT, HTH, HHT,HHH) .2×2×2 ( every time there are 2 possibilities) now lets consider a partition :

A0 :{TTT}      A1:{TTH,THT,HTT}    A2:{THH,HTH, HHT}      A3 :{HHH}

AK : set of outcomes with K heads , this is a partition of big set A

Functions:

Suppose that A and B are sets and f(A) that means inputs on element A are the outputs on element B associated with it .

We can define im ( f)={ b belonging to B } For each b we can define the inverse image (b)